Questions de théorie de l'intégration
Bonjour,
Je me permets de soumettre ces deux questions :

Pour la a), j'imagine qu'il ne suffit pas de dire que l'intégrale d'une somme est la même chose que la somme d'une intégrale.. et pour la b), je ne sais pas justifier précisément là non plus mais a-t-on, généralement, avec u et v intégrables sur un certain domaine, en intégrant sur une partie D de ce domaine et avec m et n entiers naturels premiers entre eux,
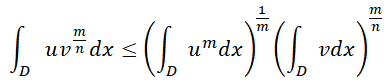 ?
?
Je me permets de soumettre ces deux questions :

Pour la a), j'imagine qu'il ne suffit pas de dire que l'intégrale d'une somme est la même chose que la somme d'une intégrale.. et pour la b), je ne sais pas justifier précisément là non plus mais a-t-on, généralement, avec u et v intégrables sur un certain domaine, en intégrant sur une partie D de ce domaine et avec m et n entiers naturels premiers entre eux,
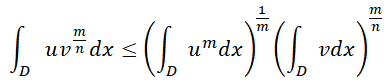 ?
? Réponses
-
Petite erreur dans ma formule, je voulais écrire u^n et 1/n et non l'inverse..
-
Pour la a), si tu ne vois pas de problème c'est que tu n'as pas bien suivi ton cours d'intégration ! À quelle condition peut-on intervertir une somme (infinie) et une intégrale ?
Pour la b), bah il existe une inégalité toute prête qui te donne ce genre d'inégalité, mais peut-être ne l'as-tu pas vue dans ton cours... -
L'inégalité dont parle Poirot pour la b)
-
Elle m'a l'air suspecte, cette série $
\displaystyle
\sum_{n=1}^{+\infty} \frac{\cos^2(nx)}{1+nx^2}
= \frac{1}{2} \cdot
\sum_{n=1}^{+\infty} \frac{1+\cos(2nx)}{1+nx^2}$, donc avec Abel... (ou même pour $x = 2k\pi$.)
D'un autre côté, $\int_0^{+\infty} \frac{dx}{1+nx^2} = \frac{1}{\sqrt{n}} \cdot \frac{\pi}{2}$... -
Oui, oui, je suis d'accord, l'égalité est vraie, mais du coup, on "calcule" les deux membres et on vérifie l'égalité, qui devient essentiellement une "coïncidence"...
J'en profite pour remarquer que $
\int_0^{+\infty} \frac{\cos^2(nx)}{1+nx} dx
=
\frac{1}{n}
\underbrace{
\int_0^{+\infty} \frac{\cos^2(t)}{1+t} dx
}_{>0}
$. -
Bah ce n'est pas une coïncidence, il y a un théorème qui permet de justifier l'égalité immédiatement et sans calcul.
-
Ah oui, d'accord c'est une série à termes positifs, merci Poirot, ça m'avait échappé !
-
Merci à vous trois, j'avais vu en effet l'inégalité de Hölder mais je n'ai pas pensé à l'utiliser ici.. Merci encore pour ces éclaircissements.
-
Pour la première égalité on peut citer Fubini sans même avoir besoin de checker la validité du théorème vu que ce qui est sous l'intégrale est positif non ?
Fubini pour des fonctions positives se pratique "à vu", me trompé-je ? -
Tu peux invoquer Tonelli ("Fubini postif") ou le théorème de convergence monotone.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres






