Jeu de dé à deux tours, répété plusieurs fois
dans Statistiques
Bonjour
Dans le cadre d’un cours d’introduction à la statistique, j’ai l’exercice suivant.
J’ai un jeu de dés, avec une mise initiale de 10. Si je fais un 6 et je gagne 50, sinon je rejoue. Là, si je fais un 6, je gagne ma mise initiale, sinon je perds. Ce qui est représenté avec l’arbre de probabilité ci-dessous.
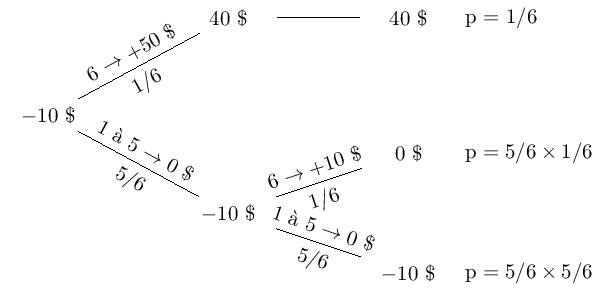
Les premières questions sont le calcul de la moyenne (-0,2778), l’écart-type (18,3312), la moyenne pour 5 jeux (-0,2778) et l’écart-type pour 5 jeux (8,1980)
La dernière question est de trouver la probabilité pour l’organisateur de faire un gain avec 100 jeux.
Ce que j’ai fait, c’est de résumer l’arbre avec l’arbre ci-dessous :
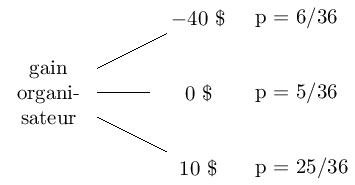
Et finalement, en considérant que 0 n’est pas un gain, cela revient à :
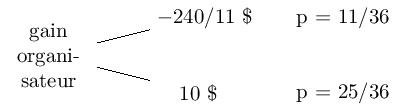
Si je considère :
\begin{align*}
x & = \text{nombre de jeux perdants}\\
y & = \text{nombre de jeux gagnants}
\end{align*} Il suffit de résoudre le système suivant.
\begin{align*}
-\frac{240}{11}x+ 10y &\ge 0\\
x+y&=100
\end{align*} Je trouve \( y \ge 68 + \dfrac{4}{7} \).
Après, il suffit de calculer : \[\sum_{k=69}^{100} P(X=k) \qquad X \sim B(100,25/36)
\] Et avec R, j’ai
Les probabilités de faire un gain avec 2, 3 et 4 jeux sont respectivement : 0.6752, 0.5760, et 0,4819.
Je pense que je ne peux simplifier les arbres comme j’ai fait. Peut-être qu’il faut que j’enchaîne deux binomiales, mais il faut aussi que je trouve le nombre de succès et d’échecs pour chacune des deux binomiales. À moins d’utiliser l’écart-type pour 100 jeux et de créer un intervalle de confiance !
Une idée de piste ?
Dans le cadre d’un cours d’introduction à la statistique, j’ai l’exercice suivant.
J’ai un jeu de dés, avec une mise initiale de 10. Si je fais un 6 et je gagne 50, sinon je rejoue. Là, si je fais un 6, je gagne ma mise initiale, sinon je perds. Ce qui est représenté avec l’arbre de probabilité ci-dessous.
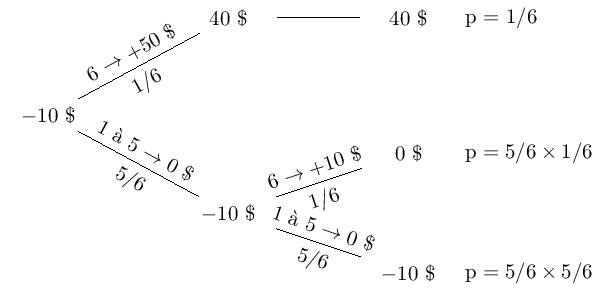
Les premières questions sont le calcul de la moyenne (-0,2778), l’écart-type (18,3312), la moyenne pour 5 jeux (-0,2778) et l’écart-type pour 5 jeux (8,1980)
La dernière question est de trouver la probabilité pour l’organisateur de faire un gain avec 100 jeux.
Ce que j’ai fait, c’est de résumer l’arbre avec l’arbre ci-dessous :

Et finalement, en considérant que 0 n’est pas un gain, cela revient à :
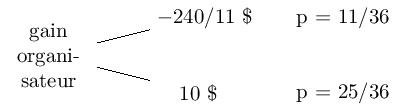
Si je considère :
\begin{align*}
x & = \text{nombre de jeux perdants}\\
y & = \text{nombre de jeux gagnants}
\end{align*} Il suffit de résoudre le système suivant.
\begin{align*}
-\frac{240}{11}x+ 10y &\ge 0\\
x+y&=100
\end{align*} Je trouve \( y \ge 68 + \dfrac{4}{7} \).
Après, il suffit de calculer : \[\sum_{k=69}^{100} P(X=k) \qquad X \sim B(100,25/36)
\] Et avec R, j’ai
P(X > 68) = dbinom(68, 100, 25/36, lower.tail = FALSE)
= 0,586433
Afin de vérifier mes calculs, j’ai fait une simulation sur un tableur pour deux jeux, et je ne retombe pas sur mes pieds.Les probabilités de faire un gain avec 2, 3 et 4 jeux sont respectivement : 0.6752, 0.5760, et 0,4819.
Je pense que je ne peux simplifier les arbres comme j’ai fait. Peut-être qu’il faut que j’enchaîne deux binomiales, mais il faut aussi que je trouve le nombre de succès et d’échecs pour chacune des deux binomiales. À moins d’utiliser l’écart-type pour 100 jeux et de créer un intervalle de confiance !
Une idée de piste ?
Réponses
-
Bonjour.
Ta modélisation est erronée. Ça se voit dans cette ligne : "Les probabilités de faire un gain avec 2, 3 et 4 jeux sont respectivement : 0.6752, 0.5760, et 0,4819." Vu ce que tu faisais avant, c'est du point de vue de l'organisateur. Or il fait un gain moyen nettement positif, qui indique que plus il joue, moins il risque d'avoir une perte.
L'erreur est de considérer comme un seul cas les gains -40 et 0. Tu "fausses le hasard".
Cordialement -
Le gain $10 X$ du joueur satisfait a
$$\Pr(X=4)=\frac{5}{36},\ \Pr(X=0)=\frac{6}{36},\ \Pr(X=-1)=\frac{25}{36},\ m=\mathbb{E}(X)=-\frac{5}{36}<0$$
Soit $\sigma^2=5,81...$ la variance de $X$
Si $X_1,\ldots,X_n$ sont les resultats de $n$ parties et si $S_n=X_1+\cdots+X_n$ alors $Z=\frac{S_n-nm}{\sigma \sqrt{n}}$ est approximativement de loi $N(0,1)$ si $n$ est grand. Donc la probabilite que l'
organisateur gagne de l'argent en 10 parties est approximativement
$$\Pr(S_n<0)=\Pr(Z<-\sqrt{n}m/\sigma)= \Pr(Z<\frac{50}{36\times 2,41})=\Pr(Z<1,73)=0,9882$$ -
gerard0 :
> L'erreur est de considérer comme un seul cas les gains -40 et 0. Tu "fausses le hasard".
Je suis totalement d’accord sur le fait que je n’aurais pas dû regrouper le -40 et le 0.
> Ta modélisation est erronée. Ça se voit dans cette ligne : "Les probabilités de faire un gain
> avec 2, 3 et 4 jeux sont respectivement : 0.6752, 0.5760, et 0,4819." Vu ce que tu faisais avant,
> c'est du point de vue de l'organisateur. Or il fait un gain moyen nettement positif, qui indique
> que plus il joue, moins il risque d'avoir une perte.
Je suis également d’accord sur le fait que plus il organise des jeux de dés, moins il risque de perdre. Mais, je ne suis pas sûr que cela signifie que la probabilité de faire des gains soit supérieure à la probabilité de faire des pertes. C’est le cas ici, mais on pourrait avoir beaucoup de petites pertes et peu de gros gains, afin qu’en moyenne il gagne, mais que la probabilité de faire des pertes soit plus grande que celle de faire des gains! -
P. écrivait : http://www.les-mathematiques.net/phorum/read.php?13,1958968,1959142#msg-1959142
[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
Merci pour la démarche, vouloir à tout prix faire une binomiale n’était pas une bonne idée. Par contre, je trouve une probabilité (56%) qui est plus proche du 50% que du 100%. Ce qui est cohérent avec ma simulation R. -
J'ai un doute sur l'énoncé proprement dit.
Si je tire un 6 :
- option 1 : je repars avec 50$\$$, donc j'ai gagné 40$\$$.
- option 2 : je repars avec 50$\$$ en plus des 10$\$$ que j'avais au début, j'ai effectivement gagné 50$\$$.
Tu as choisi l'option 1. C'est peut-être comme ça qu'il faut comprendre l'énoncé, mais je n'en sais rien.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
lourrran
C’est bien l’option 1, tu repars avec +50 auquel il faut ajouter la mise de départ -10. Bien que cela change le résultat final, que cela soit l’option 1 ou 2, ce n’est pas vraiment important. Le principal était de résoudre le problème par une loi normale et ne pas s’empêtrer dans une binomiale comme je l’avais fait :-)
[Inutile de reproduire le message précédent. AD]
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres
