Commutativement convergent => sommable?
dans Topologie
Je suis en train de chercher à me dépatouiller avec les familles sommables et les séries dans un espace vectoriel normé.
Il y a beaucoup de théorèmes, chacun simple à démontrer mais au total ça fait un peu des spaghettis. J'ai fait le dessin ci-dessous pour me retrouver. (Les remarques et corrections sont bienvenues.)
(J'ai appelé Cauchy-sommable une famille $(u_i)_{i \in I}$ telle que le filtre image du filtre des parties finies $J$ de $I$ par l'application $J \mapsto \sum_{i \in J} u_i$ soit filtre de Cauchy.)
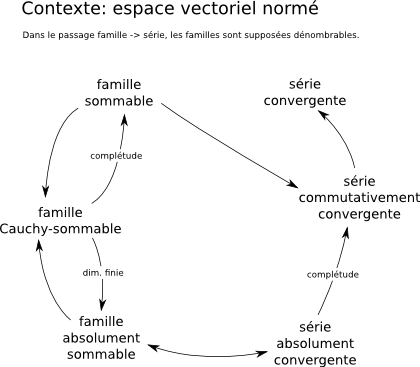
J'ai une question à ce propos. Une famille sommable correspond à une série commutativement convergente. Mais la réciproque? Si une série est commutativement convergente, la famille correspondante est-elle sommable?
Tentative de démonstration, qui termine en cul-de-sac:
Je suppose la série $\sum_{i = 0}^\infty u_i$ commutativement convergente de somme $s$.
Je suppose $r > 0$ et je cherche $J$ partie finie de $\N$ telle que pour toute partie finie $J'$ de $\N$ incluant $J$ j'aie $\| \sum_{i \in J'} u_i - s \| < r$.
Comme $\sum_{i = 0}^\infty u_i = s$, il existe $n \in \N$ tel que pour tout $n' \in \N_n$, on ait $\| \sum_{i = 0}^{n'} u_i - s \| < r$.
En posant $J = \{0...n\}$, on peut écrire $\| \sum_{i \in J} u_i - s \| < r$; et aussi, pour tout $J'$ de la forme $\{0...n'\}$ avec $n' \ge n$, on peut écrire $\| \sum_{i \in J'} u_i - s \| < r$.
Mais on voudrait pouvoir écrire $\| \sum_{i \in J'} u_i - s \| < r$ pour un $J'$ fini arbitraire incluant $J$.
Qu'à cela ne tienne! Pour un tel $J'$ donné, on choisit une permutation $\sigma$ de $\N$ qui laisse invariant $ \{0...n\}$ et qui rassemble les éléments de $J'$ supérieurs à $n$ dans les premières places après $n$, c'est-à-dire dans $\{n+1...n'\}$. On a alors $\sum_{i \in J'} u_i = \sum_{i = 0}^{n'} x_{\sigma(i)}$.
Mais ça ne marche pas, parce que $n$ a été choisi pour avoir $\forall n' \in \N_n, \| \sum_{i = 0}^{n'} u_i - s \| < r$, c'est-à-dire avec la série non permutée. La série est par hypothèse commutativement convergente, mais cela implique seulement que pour chaque $\sigma$ il existe un $n$ ayant la propriété voulue, pas que cet $n$ est indépendant de $\sigma$. Par conséquent, on ne peut écrire, pour le $\sigma$ construit ci-dessus, que forcément $\| \sum_{i = 0}^{n'} x_{\sigma(i)} - s \| < r$.
Sur la base de cet échec, j'ai essayé de construire un contre-exemple en faisant varier la valeur $n$ en fonction de $\sigma$; mais je n'ai pas réussi.
David
Il y a beaucoup de théorèmes, chacun simple à démontrer mais au total ça fait un peu des spaghettis. J'ai fait le dessin ci-dessous pour me retrouver. (Les remarques et corrections sont bienvenues.)
(J'ai appelé Cauchy-sommable une famille $(u_i)_{i \in I}$ telle que le filtre image du filtre des parties finies $J$ de $I$ par l'application $J \mapsto \sum_{i \in J} u_i$ soit filtre de Cauchy.)

J'ai une question à ce propos. Une famille sommable correspond à une série commutativement convergente. Mais la réciproque? Si une série est commutativement convergente, la famille correspondante est-elle sommable?
Tentative de démonstration, qui termine en cul-de-sac:
Je suppose la série $\sum_{i = 0}^\infty u_i$ commutativement convergente de somme $s$.
Je suppose $r > 0$ et je cherche $J$ partie finie de $\N$ telle que pour toute partie finie $J'$ de $\N$ incluant $J$ j'aie $\| \sum_{i \in J'} u_i - s \| < r$.
Comme $\sum_{i = 0}^\infty u_i = s$, il existe $n \in \N$ tel que pour tout $n' \in \N_n$, on ait $\| \sum_{i = 0}^{n'} u_i - s \| < r$.
En posant $J = \{0...n\}$, on peut écrire $\| \sum_{i \in J} u_i - s \| < r$; et aussi, pour tout $J'$ de la forme $\{0...n'\}$ avec $n' \ge n$, on peut écrire $\| \sum_{i \in J'} u_i - s \| < r$.
Mais on voudrait pouvoir écrire $\| \sum_{i \in J'} u_i - s \| < r$ pour un $J'$ fini arbitraire incluant $J$.
Qu'à cela ne tienne! Pour un tel $J'$ donné, on choisit une permutation $\sigma$ de $\N$ qui laisse invariant $ \{0...n\}$ et qui rassemble les éléments de $J'$ supérieurs à $n$ dans les premières places après $n$, c'est-à-dire dans $\{n+1...n'\}$. On a alors $\sum_{i \in J'} u_i = \sum_{i = 0}^{n'} x_{\sigma(i)}$.
Mais ça ne marche pas, parce que $n$ a été choisi pour avoir $\forall n' \in \N_n, \| \sum_{i = 0}^{n'} u_i - s \| < r$, c'est-à-dire avec la série non permutée. La série est par hypothèse commutativement convergente, mais cela implique seulement que pour chaque $\sigma$ il existe un $n$ ayant la propriété voulue, pas que cet $n$ est indépendant de $\sigma$. Par conséquent, on ne peut écrire, pour le $\sigma$ construit ci-dessus, que forcément $\| \sum_{i = 0}^{n'} x_{\sigma(i)} - s \| < r$.
Sur la base de cet échec, j'ai essayé de construire un contre-exemple en faisant varier la valeur $n$ en fonction de $\sigma$; mais je n'ai pas réussi.
David
Réponses
-
Bonjour @David,
Voici une proposition de démonstration (avec les notations que je connais). J'espère que mes explications parfois vagues suffiront, sinon elles t'aideront à demander la démonstration rigoureuse à une autre personne.
Si je dis des bétises, dis le moi !
Comme je tape tout directement, je ne connais pas tous les symboles...
Soit $E$ est un $\K$ e.v.n.
Soit $(x_n)_{n \in \N}$ une suite d'éléments de $E$.
$(x_n)_{n \in \N}$ est sommable de somme $S \iff \sum x_n$ est COMMUTATIVEMENT convergente de somme $S$
Démonstration (proposition de...) :
Point 1:
$J_0, J, K$ sont des parties finies non vides de $\N$ et $S_J=\sum_{k \in J} x_k$
Si $(x_n)$ est sommable de somme $S \in E$, soit $\sigma$ une permutation de $\N$ et $\epsilon >0$;
$\exists J_0$, $J_0 \subset J \implies ||S-S_J|| \leq \epsilon$ ; $\exists n_0, J_0 \subset \{\sigma(0), \sigma(1), \cdots, \sigma(n_0) \}$; alors
$n\geq n_0 \implies J_0 \subset J = \{\sigma(0), \sigma(1), \cdots, \sigma(n) \} \implies ||S - \sum_{0}^{n} x_{\sigma(k)} || = ||S - S_J|| \leq \epsilon$ donc $\sum x_{\sigma(n)}$ converge de somme $S$.
Point 2:
Si $(x_n)$ n'est pas sommable, on distingue deux cas :
Point 2a):
$(x_n)$ satisfait le critère de Cauchy (est-ce le bon terme ?) de sommabilité et est donc sommable dans le complété $E*$ de $E$, de somme $S \in E*-E$; alors par Point 1, $\sum x_{n}$ converge dans $E*$, de somme $S \notin E$, et ne converge donc pas dans $E$; a fortiori, $\sum x_{n}$ n'est pas commutativement convergente dans $E$
Point 2b):
$(x_n)$ ne satisfait pas le critère de Cauchy:
$\exists \epsilon > 0, \forall J, \exists K, J \cap K = \varnothing$ et $||S_K|| \geq \epsilon$ et alors :
$\exists K_0, ||S_{K_0}|| \geq \epsilon$ ; soit $k_0 = max K_0 : K_0 \subset 0, k_0$
$\exists K_1, 0, k_0\cap K_1=\varnothing$ et $||S_{K_1}|| \geq \epsilon$; soit $k_1 = max K_1 : k_1 > k_0$ et $K_1 \subset k_0 + 1, k_1$;
$\exists K_2, 0, k_1\cap K_2=\varnothing$ et $||S_{K_2}|| \geq \epsilon$; soit $k_2 = max K_2 : k_2 > k_1$ et $K_2 \subset k_1 + 1, k_2$;
$\cdots$
où l'on a définit par récurrence une suite $(K_p)$ de parties finies non vides de $\N$ et la suite strictement croissante de leurs maximum $(k_p)$ telles que, avec $k_{-1} = -1$ :
$\forall p \in \N, K_p = \{a_{p,1}, \cdots, a_{p,d_p}\} \subset U_p = k_{p-1}+1, k_p$ et $||S_{K_p}|| \geq \epsilon$ ;
pour $p$ fixé, on définit $\pi$ sur $U_p$ de sorte que $\pi_{|U_p}$ soit une permutation de $U_p$ et que :
$\forall j = 1, \cdots, d_p : \pi(k_{p-1} + j) = a_{p,j}$ ;
On a donc défini une permutation $\pi$ de $\N$ telle que dans la suite $(x_{\pi(n)})$ les éléments $x_j$ pour lesquels $j \in K_p$ deviennent consécutifs, et ce pour chaque entier $p$ ; alors la série $\sum x_{\pi(n)}$ contient une infinité de tranches de Cauchy de normes $\geq \epsilon$, et n'est donc pas convergente. Ouff!
[Au lieu de "\inter", il faut mettre "\cap" et l'ensemble vide s'obtint par "\emptyset" ou, plus joli par "\varnothing". Bruno] -
Merci Yves. Je vais examiner ça.
David -
Bonsoir,
1) Sommable implique commutativement convergente.
2) Commutativement convergente implique sommable.
Je ne sais pas si ce que je vais dire aidera car je parle d'un cas particulier (l'espace normé est R).
Dans ce cas on utilise les termes "absolument convergente" (AC) et "commutativement convergente" (CC).
J'ai besoin aussi de la notion "semi convergente" (SC) (qui veut dire convergente mais pas AC).
On démontre alors :
1') AC implique CC
2') CC implique AC
Pour démontrer le 2') on peut démontrer sa contraposée.
Si une serie est SC, alors elle n'est pas CC.
Ça se fait en quelques étapes :
A - on démontre que la serie des termes positifs (respectivement négatifs) de la suite divergent vers l'infini (resp. -l'infini).
B - on construit une suite, en réordonnant les termes de la suite originale par exemple de la manière suivante :
On choisit les termes positifs jusqu'à 10, puis on choisit un terme négatif.
On choisit les termes positifs suivants jusqu'à 20, puis un terme négatif.
Etc. C'est un algorithme.
C - on démontre que ça diverge
(On peut aussi faire en sorte que ça converge vers le réel que l'on veut grâce au fait que la semi convergence implique que le terme général tend vers 0).
Mon intervention est sûrement naïve mais elle pourra peut-être donner des idées (au moins pour tenter de prouver la contraposée).
Evidemment difficile de parler de positif/négatif pour C, par exemple, alors pour E e.v.n. quelconque...
Pardon pour l'éventuel hors sujet.
Cordialement. -
Les deux notions ne sont-elles pas équivalentes à celle-ci : Pour tout $\epsilon > 0$, il existe une partie finie telle que toute somme finie d'éléments en dehors de cette partie ait une norme $\leq \epsilon $ ?
-
Les deux notions ne sont-elles pas équivalentes à celle-ci : Pour tout $\epsilon > 0$, il existe une partie finie telle que toute somme finie d'éléments en dehors de cette partie ait une norme $\leq \epsilon $ ?
Ça, c'est la propriété de Cauchy pour une famille sommable. (Ce que j'ai appelé la Cauchy-sommabilité.)
Si l'espace est complet (Banach) elle implique la sommabilité. En dimension finie (auquel cas l'espace est forcément complet), elle implique aussi l'absolue sommabilité.
David -
Merci à Dom. Ca règle le cas pour $\R$, et sans doute pour un espace à dimension finie, sur $\R$ ou sur $\C$.
Mais dans le cas général?
J'essaye de comprendre la démonstration d'Yves, mais pour le moment, je n'arrive pas loin. -
Et si on passe au complété, genre "(Cauchy-)sommable dans le complété et limite dans le complété appartenant à l'espace lui-même" ?
Est-ce alors équivalent aux deux noitions ? -
Si au départ on sait que la série est commutativement convergente, ça veut dire que sa somme existe pour toute permutation des indices, et en plus qu'elle est la même.
Donc la somme, on l'a sous la main. Si de fait commutativement convergent implique sommable, ce sera forcément vers cette même somme, vu qu'on sait déjà en sens inverse que toute famille sommable correspond à une série commutativement convergente vers la même somme.
Donc le passage au complété n'apportera rien, à mon avis.
David -
Bonjour à tous,
@bosio frederic, le passage au complété est effectivement partie de la démonstration que je propose (Point 2b), qui est LE point crucial et difficile de cette démonstration.
Quand je dis difficile, en fait ça ne l'est pas. On part de la définition que la suite ne satisfait pas le critère de Cauchy, mais pour conclure il faut avoir l'idée de définir la permutation $\pi$.
La démonstration est imparable. Je suis étonné si elle n'est pas dans tous les bons livres. Je ne l'ai pas inventée, seulement eue en cours !
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.2K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 65 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 314 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres

