Contrexemple "naturel" en topologie

omega · May 2021

Bonjour

Je cherche un exemple assez naturel d'une application surjective $f : X \to Y$ entre espaces topologiques qui est continue, surjective et telle qu'il existe une partie $A\subset Y$ non ouverte telle que $f^{-1}(A)$ est ouverte.

Je sais répondre à ma question en munissant $X$ de la topologie discrète. Mais ce n'est pas ce que je cherche, car dans ma vie mathématique, les espaces topologiques que je côtoie ne sont pas munis de la topologie discrète.

C'est un peu ça que je veux dire par "assez naturel", je cherche un exemple qui ne soit pas construit ad hoc, mais qui se rencontre dans des cadres mathématiques autres que "je m'amuse à construire des contre-exemples pathologiques". Un truc qu'on puisse croiser dans des questions d'analyse ou de géométrie par exemple.

Si vous avez ça en magasin...

Bonne semaine.

marco · May 2021

Bonjour,

Soit $f$ la fonction de $\R$ dans $\R$, qui à $x$ associe $x^3-x$. Alors elle est continue et surjective. $f$ atteint un minimum local en $x_0=\frac{1}{\sqrt{3}}$. Soit $B=]x_0-\epsilon,x_0+ \epsilon[$, et $A=f(B)$, alors $A$ n'est pas un ouvert, et $f^{-1}(A)=B$ est ouvert.
(on choisit $\epsilon$ assez petit par exemple $\epsilon=-\frac{1}{\sqrt{3}}$)

omega · May 2021

Merci Poirot

Mais $f^{-1}(\{0\})= [0,1]$ qui n'est pas un ouvert de $[0,2]$,il me semble. Ou j'ai mal compris ?

Après, on peut faire marcher ton truc en prenant $[0,2]\setminus\{1\}$ dans l'espace de départ, la fonction reste surjective, et l'image réciproque de $\{0\}$ est $[0,1[$ qui est bien un ouvert de $[0,2]\setminus\{1\}$.

Ouais, on s'en sort avec des trucs comme ça. Bon j'aurais aimé un truc un peu moins bricolé, parce que là, je prends une fonction continue et je retire juste des points à l'espace de départ pour que ça marche, mais en pratique, la vraie fonction naturelle qu'on regarde ne vérifie pas la propriété.

EDIT : Poirot, tricheur, tu as supprimé ton message !

NoName · May 2021

Regarde l'image du milieu, qui j'espere sera suffisament explicite.
(En gros c'est le contre exemple canonique au fait que les immersions injectives n'ont pas pour image une sous variété)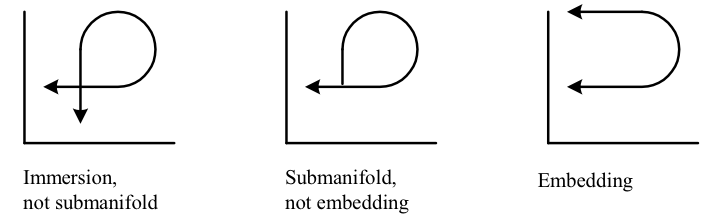
40.immersions.png

omega · May 2021

marco : je ne suis pas sûre de bien comprendre, $f^{-1}(A)$ n'est pas égal à $B$ il y a aussi un intervalle semi-ouvert contenu dans $]-\infty, -1[$ dans $f^{-1}(A)$, non ?

marco · May 2021

Oui, mon exemple est faux.

D'après NoName, on peut aussi choisir $f:[0, 2\pi [ \rightarrow U(1)$ qui à $t$ associe $e^{it}$. Et $B=[0,\pi[$ et $A=f(B)$, alors $A$ n'est pas ouverte dans $U(1)$ et $B$ est bien ouvert dans $[0,2\pi[$.

Poirot · May 2021

J'avais mal lu l'énoncé, j'ai donc caché mon message, mea culpa !

NoName · May 2021

Si tu préfères, prends la fonction $f: \mathbb{R}\to \mathbb{C}$ qui à $t$ associe $1+t$ pour $t\leq 0$ et $\exp(i.\arctan(t))$ pour $t\geq 0$, que tu restreins à son image.

omega · May 2021

Merci Marco. Simple élégant et bien vu comme d'habitude ! [small]D'ailleurs en ouvrant ce fil, j'espérais bien que tu y jetterais un œil...8-)[/small]

NoName, merci de t'intéresser à mon problème, mais je ne comprends pas bien ton exemple. Je connais ce contrexemple d'immesion injective qui n'est pas un plongement, mais je ne vois pas comment construire mon ensemble $A$.

Bon en tout cas, j'ai eu la réponse à ma question par Marco.

Merci à tous et bonne semaine !

NoName · May 2021

Mon exemple et celui de Marco sont le même.
L'application définie par Marco est un immersion injective qui n'est pas ouverte.
L'exemple que je donne (sous forme de dessin ou par la description explicite, à noter qu'il manque un $2$ devant l'arctan dans ma formule explicite) est du meme tonneau.
Regarde l'image de $]-1-r, -1+r[$ pour un $r>0$ par la fonction $f$, ca n'est pas un ouvert (tout ouvert contenant $f(-1)$ contient une réunion $f(]-1-r, -1+r[)\cup f(]T, \infty[)$) mais son image inverse est $]-1-r,-1+r[$ qui est un ouvert de $\mathbb{R}$.