Transformée de distances - Python
Bonjour à tous
Pour un devoir en imagerie numérique, j'ai deux ensembles de points dans le plan, disons S1 et S2, et je dois trouver le point de S1 le plus éloigné de tous les points de S2 et vice versa
À travers mes recherches, j'ai trouvé des lectures intéressantes sur des transformées de distances mais je n'ai pas tout compris ; j'ai aussi entendu parler de distance de Hausdorff mais je ne sais pas si c'est utile.
Je recherche donc des documents utiles, des explications ou même d'autres idées pour résoudre ce problème.
Merci.
Pour un devoir en imagerie numérique, j'ai deux ensembles de points dans le plan, disons S1 et S2, et je dois trouver le point de S1 le plus éloigné de tous les points de S2 et vice versa
À travers mes recherches, j'ai trouvé des lectures intéressantes sur des transformées de distances mais je n'ai pas tout compris ; j'ai aussi entendu parler de distance de Hausdorff mais je ne sais pas si c'est utile.
Je recherche donc des documents utiles, des explications ou même d'autres idées pour résoudre ce problème.
Merci.
Réponses
-
Bonjour.
La distance dans le plan est classique (distance euclidienne) et si tu as les coordonnées des points de S1 et S2, un algorithme élémentaire répond à la question (test point par point). Comme cet algorithme est polynomial en les données, il peut convenir si tu n'as pas trop de points.
Cordialement. -
Bonjour,
il n'y a rien de compliqué en soit, comme cela a été dit, il suffit de calculer la norme Euclidienne et d'en rechercher les $min$ et $max$; j'ai déjà fait ça en 3D entre une sphère et une surface "selle" (d'aucuns comprendront que j'ai utilisé la vectorisation: 2290 points d'un côté et 2500 de l'autre, soit 5.725 million de combinaisons et moins d'une seconde pour trouver le $min$):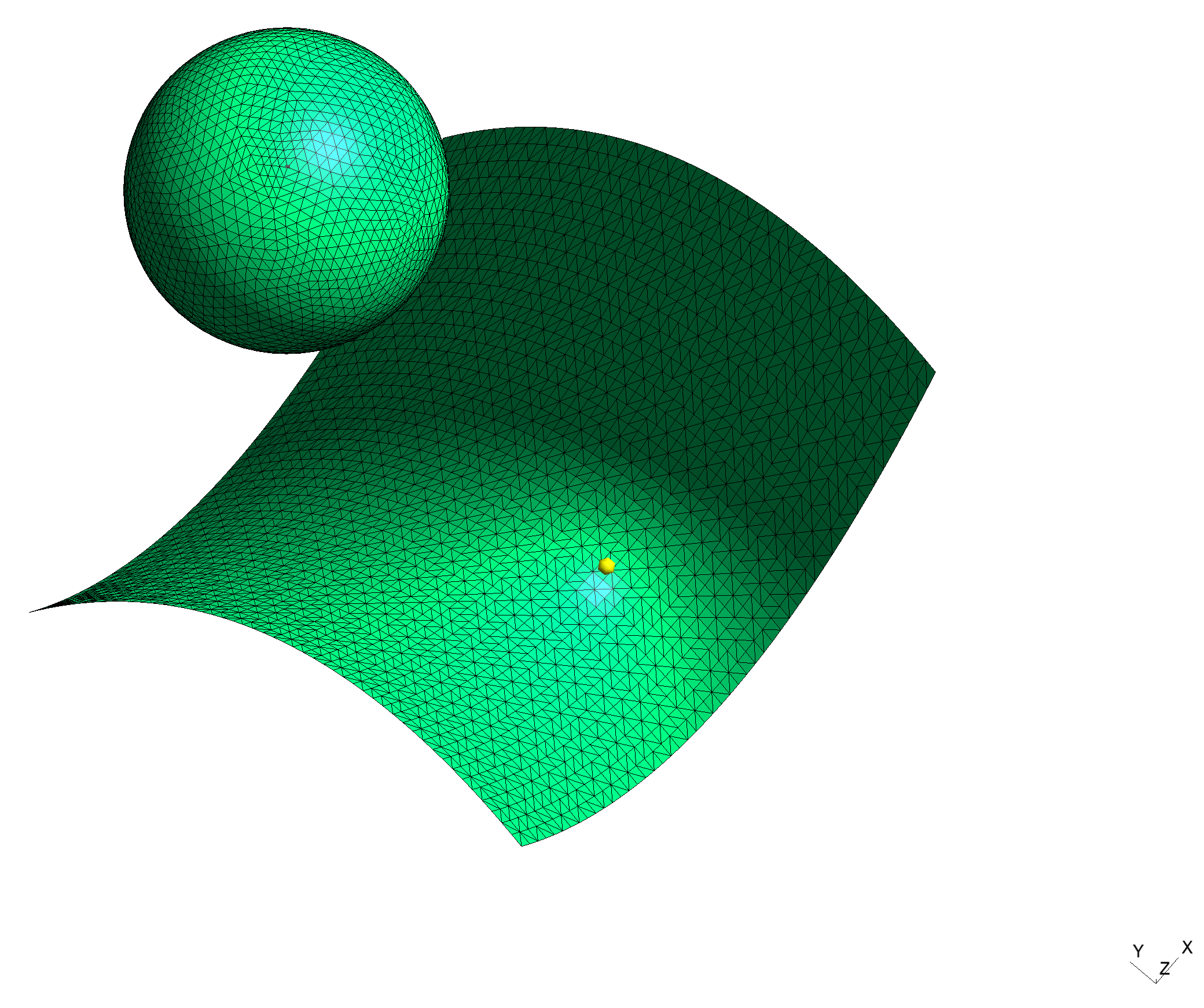
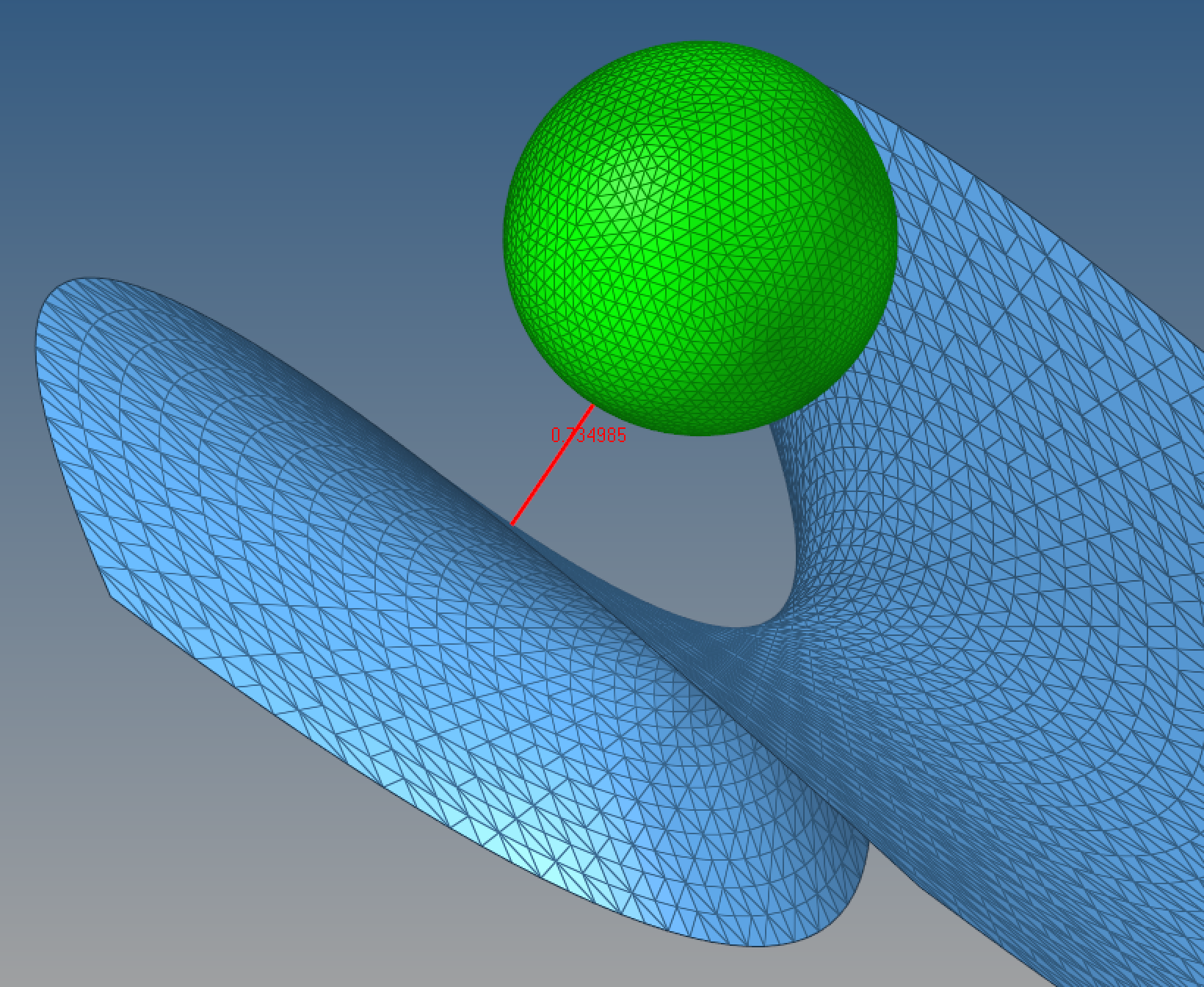
The minimum distance has been found to 0.7349854707717896 the 5725000 calculations took 0.3877909183502197 second
La seule limite que je vois c'est le nombre de points, et la taille du vecteur $distance$ qui en résulte (ici 5.725 million de lignes pour un problème 3D)
Paul -
Merci pour vos réponses
J'aurais dû préciser que bien sûr je sais qu'un balayage de tous les points résout le problème, mais vu que c'est d'une complexité quadratique, j'étais justement à la recherche d'un algorithme plus performant -
Peut-être en cherchant un point sur l’enveloppe convexe de tes ensembles.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
@nicolas.patrois tu peux développer s'il te plait ?
Je n'ai pas saisi ce qu'il faut faire après avoir trouvé mes ensembles convexes. -
Pour des ensembles à priori quelconques, je doute qu'autre chose qu'un balayage exhaustif permette de conclure (*). Pour des ensembles structurés, il peut y avoir des algorithmes bien plus efficaces, mais liés à la structure.
L'enveloppe convexe est utile si les deux nuages de points sont nettement séparés, pas s'ils se mélangent. Et la recherche de cette enveloppe peut être coûteuse.
Cordialement.
(*) comment savoir si l'introduction d'un nouveau point va changer la réponse ? -
Oui je vois
Et là mes nuages de points n'ont aucune raison d'être disjoints. -
L'idée sous-jacente de l'approche par des surfaces convexes/surfaces de réponse est de chercher le minimum, extremum qui n'est pas nécessairement (et rarement) un des points fournis; il faut en connaître a priori les caractéristiques pour en recaler les paramètres.
L'approche (simpliste mais exhaustive) que je propose, est de tester l'ensemble des combinaisons possibles en créant 2 vecteurs d'indices (1 par surface); l'image ci-dessous en résume le principe (image issue du cas que j'ai présenté précédemment); l'astuce réside dans la création de ces vecteurs sans l'aide d'aucune boucle B-)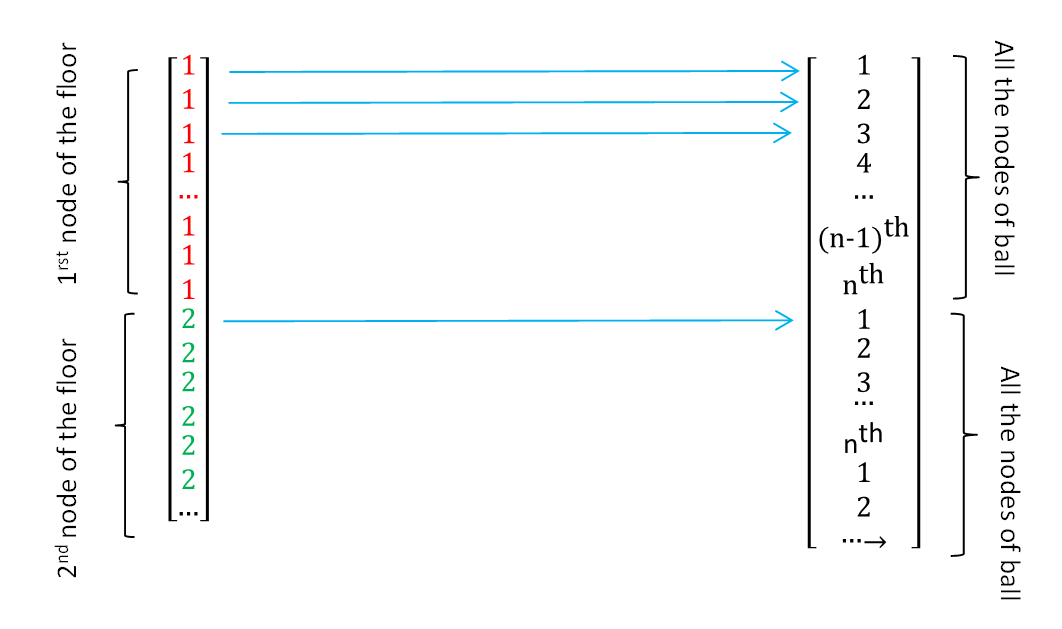
Paul -
Ah je comprends le principe ! Simple et efficace.
Mais comment créer ces 2 vecteurs (de taille très grande au vu de ce que j'ai compris) en l'occurrence sur python, sans utiliser de boucle -
Ah et je viens de remarquer que ça a l'air de faire écho à un de tes précédents posts
Mais peux-tu réexpliquer le principe stp? -
Je travaille ici sur les indices des tableaux/matrices des points des différentes surfaces; en Français cela se traduit par :
- point $P_1$ de $S_1$ pointe le point $P'_1$ de $S_2$
- point $P_1$ de $S_1$ pointe le point $P'_2$ de $S_2$
- ...
- puis
- point $P_2$ de $S_1$ pointe le point $P'_1$ de $S_2$
- et ainsi de suite
import numpy as np n1 = 2 # nombre de points de la surface 1 n2 = 5 # nombre de points de la surface 2 i1 = np.arange(0,n1, dtype = np.int) # [0 1 2 ... n1] i2 = np.arange(0,n2, dtype = np.int) # [0 1 2 ... n2] j1 = np.ones(n2, dtype = np.int) # vecteurs unitaires qui servent au produit de Kronecker j2 = np.ones(n1, dtype = np.int) indice1 = np.kron(i1,j1) # vecteur d'indices pour les points de S1 indice2 = np.kron(j2,i2) # idem pour S2 print("indice 1 = {}".format(indice1)) print("indice 2 = {}".format(indice2))Comme montré dans ce fil, il ne reste plus qu'à utiliser ces indices pour calculer un vecteur "distance" et d'en rechercher ensuite les $\min$ et $\max$.
Aucune boucle n'a été utilisée B-)
Paul -
Ok merci !
Je vais de ce pas essayer de mettre en place cela et voir si c'est bien plus efficace que des boucles imbriquées -
nice_boycott a écrit:Je vais de ce pas essayer de mettre en place cela et voir si c'est bien plus efficace que des > boucles imbriquées
Assurément (par expérience) et donc si tu trouves mieux sans utiliser des artifices comme Numba par exemple, ça m’intéresse -
Juste pour éclaircir : tu cherches bien $\max_{x\in S_1}(\min_{y\in S_2} d(x,y))$ ?
-
Bonjour
J'ai effectivement essayé de m'initier à la vectorisation du problème mais je rencontre quelques difficultés :
- les vecteurs indices ne semblent convenir que pur un problème en dimension 1, mais là j'ai des points à deux coordonnées ;
- comment supprimer les indices qui ne m'intéressent pas, par exemple le point (0,0) ne fait partie d'aucun de mes ensembles, que faire ?
J'espère ne pas m'être trompé dans la compréhension de ce processus de vectorisation car il me semble très intéressant. -
GaBuZoMeu écrivait : http://www.les-mathematiques.net/phorum/read.php?15,1912892,1914426#msg-1914426
[Inutile de recopier l'avant-dernier massage. Un lien suffit. AD]
En effet oui je crois que mathématiquement c'est bien ça que je cherche. -
il ne s'applique pas qu'à un problème 1D (voir mon exemple avec 2 surfaces en 3D); ne pas oublier qu'on travaille sur des tableaux/matrices de type $A_{i,j}$ où $i$,$j$ sont tes indices: par exemple $A[1,1]$ en Python pointe sur $A_{2,2}$.
En vectorisation, on ne travaille pas sur 1 indice, mais un "bloc" d'indices qu'on appelle "vecteur" !
Je ne saurais trop te conseiller d'aller voir le fil précédemment cité où tu trouveras des exemples -
Il me semble que paul18 parle de $\min_{x\in S_1}(\min_{y\in S_2} d(x,y))$. Me trompé-je ?
-
GaBuZoMeu Il me semble que paul18 évoque à la fois le min et le max
-
Il évoque $\min_{x\in S_1}(\min_{y\in S_2} d(x,y))$ et $\max_{x\in S_1}(\max_{y\in S_2} d(x,y))$, si je ne m'abuse (prendre le min ou le max sur les distances de tous les couples d'un point de $S_1$ et d'un point de $S_2$), mais pas $\max_{x\in S_1}(\min_{y\in S_2} d(x,y))$. Me trompé-je ?
-
Comme il parle de la distance de Hausdorff…Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
Qui, "il" ? Je n'ai pas vu que Paul18 parle de distance de Hausdorff ... Ai-je loupé quelque chose ?
-
nice_boycott si, mais c’est vrai que son message n’est pas très clair.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
à la base je cherche un moyen de trouver la distance la plus grande qui soit entre deux points issus respectivement de deux nuages de points dans le plan. Du coup j'interprète peut-être mal les notations mathématiques que tu as données GaBuZoMeu
-
Alors ce n’est pas la distance de Hausdorff mais le max des max.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
Cela dit je mentionnais juste la distance de Hausdorff comme une de mes lectures lors de mes recherches sur le sujet.
Mais merci pour cette précision mathématique :-)
J'ai juste une question sur le vecteur distance (j'ai enfin compris l'implémentation des vecteurs indice1 et indice 2 mais je bute sur le vecteur distance).
J'avais pour idée de créér une fonction distancedef distance(u,v): '''calcule la distance entre deux couples de points u et v''' return ((u[0]-v[0])**2 + (u[1]-v[1])**2)**0.5
puis de l'appliquer comme cecidist = distance(S1[indice1], S2[indice2])
mais sans succèsarray([8.06225775, 2. ])
(avec pour entrées de testS1 = np.array([[2, 5],[1, 2]]) S2 = np.array([[9, 5],[6, 7],[0, 4]]) indice1 = [0 0 0 1 1 1] indice2 = [0 1 2 0 1 2]
)
Je sais que je ne maîtrise absolument pas les subtilités de la programmation python mais pourriez vous m'aider s'il vous plaît ? -
Déjà, dans un but d’économie de moyens, la racine carrée est inutile puisque tu veux juste comparer les distances, donc leurs carrés.
Pour le reste, je ne connais pas assez numpy.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
Nul besoin de fonction (cela fonctionne avec, mais ce n'est pas obligatoire); l'exemple ci-dessus devrait t'aiguiller je pense; j'y ajoute une image supplémentaire.
import numpy as np n = 10 A = np.arange(n) A = A.reshape( (int(0.5*n),2), order='f') X = A[:,0] Y = A[:,1] Norme= np.sqrt(X**2 + Y**2) mini = np.min(Norme) maxi = np.max(Norme) print("Norme = {}".format(Norme)) print("min = {}".format(mini)) print("max = {}".format(maxi))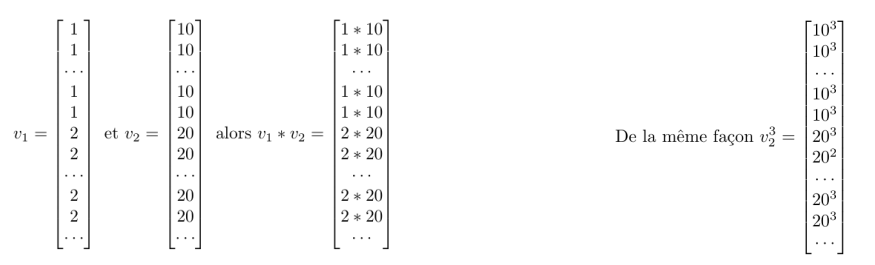
On voit bien qu'il en résulte un vecteur "norme" dans lequel on cherche le $min$ et le $max$; le boulot c'est de mettre sous forme de tableau tes points, et ensuite de calculer la norme de tous les vecteurs possibles (voir les posts précédents).
Amuse-toi à mettre n à 1 million (en commentant le premier print), et tu verras que c'est pratiquement instantanné
Paul -
En supposant que Points_S1 et Points_S2 sont les tableaux avec les coordonnées des points,alors ce bout de code devrait fonctionner; attention, dans le cas présent, les $X$ sont dans la $2^{ième}$ colonne (voir [:,1]) et les $Y$ dans la $3^{ième}$ (voir [:,2]).
Les termes "indice" regroupent en fait les différentes combinaisons (on fonctionne par "ligne" comme on le voit sur l'image précédente) et $k$ balaie les vecteurs indice1 et indice2 de la première à la dernière ligne.
J'espère que ça te laisse entrevoir les possibilités de la vectorisation (j'utilise sensiblement toujours le même raisonnement, et je suis loin d'en maîtriser toutes les subtilités)
Pauln1 = np.shape(Points_S2)[0] n2 = np.shape(Points_S1)[0] i1 = np.arange(0,n1, dtype = np.int) i2 = np.arange(0,n2, dtype = np.int) j1 = np.ones(n2, dtype = np.int) j2 = np.ones(n1, dtype = np.int) indice1 = np.kron(i1,j1) indice2 = np.kron(j2,i2) NbreCombinaisons = np.shape(indice1)[0] k = np.arange(0,NbreCombinaisons, dtype = np.int) # Normes = np.sqrt( (Points_S1[indice2[k], 1] - Points_S2[indice1[k], 1])**2 + \ (Points_S1[indice2[k], 2] - Points_S2[indice1[k], 2])**2 ) MinDistance = np.min(Normes) MaxDistance = np.max(Normes) -
Ah ça y est j'ai réussi!
Au fait paul18 ton algo poussé à l’extrême (1000000) me renvoie des NotANumber mais cette limite est largement suffisante pour l'utilisation que je vais en faire.
Merci à tous -
comment peux-tu avoir des Nan avec des termes au carré et aucune division? tu es sûr de tes données? tu pointes bien vers les coordonnées?
Le code ci-dessous donne plus de 42 million de combinaisons sans NaNimport numpy as np import time n1 = 20_099 n2 = 2_103 Points_S1 = np.random.random( (n1,3)) Points_S2 = np.random.random( (n2,3)) t0 = time.time() n1 = np.shape(Points_S1)[0] n2 = np.shape(Points_S2)[0] i1 = np.arange(0,n1, dtype = np.int) i2 = np.arange(0,n2, dtype = np.int) j1 = np.ones(n2, dtype = np.int) j2 = np.ones(n1, dtype = np.int) indice1 = np.kron(i1,j1) indice2 = np.kron(j2,i2) NbreCombinaisons = np.shape(indice1)[0] k = np.arange(0,NbreCombinaisons, dtype = np.int) Normes = np.sqrt( (Points_S1[indice1[k], 1] - Points_S2[indice2[k], 1])**2 + \ (Points_S1[indice1[k], 2] - Points_S2[indice2[k], 2])**2 ) MinDistance = np.min(Normes) MaxDistance = np.max(Normes) print("Min = {}".format(MinDistance)) print("Max = {}".format(MaxDistance)) print("Nombre de combinaisons = {}".format(np.shape(k)[0])) t1 = time.time() T1 = t1 - t0 print("Durée : {}".format(T1)) del j1; del j2; del k; del NormesMin = 8.506638984615577e-05 Max = 1.3916897858871962 Nombre de combinaisons = 42268197 Durée : 8.254205465316772
-
Je parle du code qui précède le dernier que tu as envoyé, celui qui servait d'exemple avec le tableau A
Voici le résultat avec n = 100000Norme = [nan nan nan ... nan nan nan] min = nan max = nan
-
voir dernier apport; quant au code avec A, il fonctionne chez moi (Anaconda et Spyder)
-
Cette histoire de NaN me travaillait, et j'ai pu reproduire le problème; bizarrement c'est au niveau de np.min et np.max que ça plantait. J'ai finalement solutionné le problème en forçant le type de $A$ en np.int64, comme quoi on peut se faire avoir sur les conversions automatiques de types.
Maintenant cela fonctionne (je me suis arrêté à 1 milliard dans le cas présent)import numpy as np n = 1_000_000_000 A = np.arange(n, dtype = np.int64) A = A.reshape( (int(0.5*n),2), order='f') X = A[:,0] Y = A[:,1] Norme= np.sqrt(X**2 + Y**2) mini = np.min(Norme) maxi = np.max(Norme) # print("Norme = {}".format(Norme)) print("min = {}".format(mini)) print("max = {}".format(maxi)) -
je dois trouver le point de $S_1$ le plus éloigné de tous les points de $S_2$ et vice versa
Ce n'est pas pareil. Première chose : spécifier clairement le problème.je cherche un moyen de trouver la distance la plus grande qui soit entre deux points issus respectivement de deux nuages de points dans le plan
Pour ne pas être uniquement négatif, une piste qu'il vaudrait peut-être le coup d'explorer pour éviter le calcul de $|S_1|\times |S_2|$ distances.
Ça ne coûte pas très cher de subdiviser la région du plan occupée par les points en petits carrés indexés par des couples d'entiers $(i,j)$ et de ranger les points de $S_1$ et ceux de $S_2$ dans ces carrés. C'est en gros en $n\log(n)$ si les deux paquets de points sont de taille $n$.
Supposons que c'est bien $\max_{x\in S_1,y\in S_2} d(x,y)$ que l'on cherche, Si on s'intéresse alors aux distances d'un $x_0\in S_1$ aux $y\in S_2$ il est inutile de s'embêter à calculer les $d(x_0,y)$ pour $y$ dans un carré proche de celui de $x_0$. La proximité entre le carré $(i_0,j_0)$ et le carré $(i,j)$ peut s'évaluer par $|i-i_0|+|j-j_0|$. Si on a déjà parcouru un bout de la liste des points de $S_1$ et qu'on a un record partiel de distance quand on arrive à $x_0$, je me dis que ça évite un gros paquet de calculs (surtout si on a commencé d'éplucher la liste des points de $S_1$ par ceux qui sont le plus en bas à gauche et la liste des points de $S_2$ par ceux qui sont le plus en haut à droite).
Ça demande à être beaucoup retravaillé, mais ça me semble une piste valable. -
Tout d'abord je m'excuse car c'est vrai que je n'ai pas énoncé mon problème tel que je me le suis représenté
Ensuite merci de me proposer ton idée car j'ai envie d'approcher plusieurs pistes. As-tu une façon de subdiviser mes nuages de points en carré avec une telle complexité? -
C'est simple : on trie la liste des abscisses de l'ensemble de points, ce qui permet de donner le n° de colonne dans la grille de carrés, et on trie la liste des ordonnées, ce qui permet de donner le n° de ligne dans la grille de carrés. Tu connais la complexité des bons algorithmes de tri.
-
Pour la plus grande distance, est-ce qu'on peut dire qu'elle concerne les nœuds en périphérie des 2 surfaces?
Au risque d'être hors sujet, il y a la librairie "ConvexHull" qui fait ce type de boulot, non ? -
ConvexHull (enveloppe convexe) et pas ConvexHill (colline convexe). ;-)
À part ça, oui : soit $C$ est l'enveloppe convexe du nuage de points $S$ et $x$ un point quelconque. Si $y_0\in S$ réalise le maximum des $d(x,y)$ pour $y\in S$, alors $y_0$ est un sommet de $C$. En effet, $S$ est entièrement contenu dans le disque fermé de centre $x$ et de rayon $d(x,y_0)$, donc $C$ aussi puisque le disque est convexe ; et comme le disque est strictement convexe, $y_0$ est forcément un sommet de $C$.
Le calcul de l'enveloppe convexe de $n$ points dans le plan se fait en $O(n\log(n))$. Est-ce qu'on économise beaucoup en faisant ça ? Ça dépend de la forme du nuage de points. Si par exemple les points sont répartis sur un cercle, pas tellement. -
j'ai corrigé (touches u et i sont la distance la plus courte sur mon clavier ;-) )
En pratique (pour la plus grande distance), il suffit juste de récupérer les points sur chaque périphérie et d'en calculer la norme Euclidienne.
Autre idée tordue qui me vient pour la plus petite distance: si on superpose les 2 surfaces via un simple changement de repère "bien choisi"? un simple trie lexicographique sur $X$ et $Y$ devrait mettre en lumière les points les plus proches ?!?! (je n'ai pas testé) -
Pour l'idée des surfaces convexes, le fait que les deux nuages de points se "rencontrent" on va dire ne rend pas le problème plus complexe ?
Et pour l'idée du tri lexicographique, peux-tu en expliquer le principe s'il te plaît (elle consiste d'après ce que tu en dis à la recherche du minimum, ce qui s'éloigne un peu de mon problème de base, mais ça m'intéresse quand même) -
Comme je l'ai déjà dit, on peut ne pas gagner beaucoup en "récupérant les points sur chaque périphérie", c.-à-d. en calculant les sommets de l'enveloppe convexe (exemple extrême des points situés sur un cercle)En pratique (pour la plus grande distance), il suffit juste de récupérer les points sur chaque périphérie et d'en calculer la norme Euclidienne. -
GaBuMoZeu excuse moi mais je n'ai pas compris en quoi le tri des abscisses et des ordonnées va nous diviser les ensembles en carrés
-
Supposons que le nuage de points soit compris dans le rectangle $[0,24]\times [0,15]$, qu'on divise en $24\times 15= 360$ carrés de 1cm de côté. Le carré $[i,i+1]\times [j,j+1]$ est repéré par le double indice $(i,j)$.
On trie maintenant la liste des abscisses des points augmentée des entiers de $0$ à $24$. Tous les points dont l'abscisse, dans la liste triée, se trouve entre l'entier $i$ et l'entier $i+1$ sont dans des carrés de premier indice $i$.
On procède de même pour les ordonnées. Ça nous donne le deuxième indice du carré dans lequel se trouve chaque point du nuage. -
Ok je vois
Penses-tu aussi que les côtés des carrés a son ont leur importance ?
Peut-être est-ce juste en expérimentant que je le saurai ou y a-t-il un moyen de trouver la longueur de côté optimale ? -
Ça dépend du nuage de points.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres



