L'implication

Mister Da
Mister Da
dans Fondements et Logique
Bonjour,

je n'ai aucune culture en logique et n'y connais vraiment pas grand chose. J'ai toujours vu les propositions $P_1\colon p\Rightarrow q$, $P_2\colon \lnot q\Rightarrow \lnot p$ et $P_3\colon \lnot p \lor q$ comme logiquement équivalentes, c'est-à-dire qu'elles ont la même table de vérité $$

\begin{array}{cccc}
&p & q & P_i\\
1.&V & V & V\\
2.&V & F & F\\
3.&F & V & V\\
4.&F & F & V
\end{array}

$$ sans jamais trop me poser de question (en fait je me dis secrètement que $P_3$ est la définition même de $P_1$...).

Je profite du confinement pour être un peu moins ignorant. Dans mon esprit le modus ponens ($p, p\Rightarrow q \vdash q$) correspond au deux premières lignes de la table de vérité alors que le modus tollens ($\lnot q, p\Rightarrow q \vdash \lnot p$) correspond aux lignes 2 et 4.
Du coup, si on retourne un peu au "fondement" de tous ça, est-ce parce qu'on admet le modus ponens et le modus tollens qu'on peut dire que les propositions $P_1$, $P_2$ et $P_3$ sont (logiquement) équivalentes ?

J'espère que ma question est compréhensible.
Je vous remercie par avance pour vos lumières.
Cordialement,
Mister Da.

Réponses

  • christophe c
    christophe c
    Non, c'est parce qu'on admet que $$

    \forall p: [non(non(p)) \iff p]

    $$ L'implication $(a\to b) \to (\neg b \to \neg a)$ est intuitionniste (ie "constructive" in some sense), mais la réciproque : $$

    (\neg b \to \neg a)\to (a\to b)

    $$ est équivalente au tiers exclus.
    De même affirmer : $$

    \forall a,b: [(a\to b)\iff ((non(a))\ ou\ b)]

    $$ équivaut à affirmer le tiers exclus
    Par contre, of course, l’implication $([\neg a]\ ou\ b)\to (a\to b)$ est intuitionniste.

    Pour comprendre tout ça, c'est très simple : au lieu de vrai faux, les valeurs des phrases sont des ouverts d'un espace topologique (quelconque) :
    $a\ ou\ b$ est la réunion des ouverts $a,b$, ie c'est $a\cup b$
    $non(a)$ est l'intérieur du complémentaire de $a$
    $a\to b$ est la réunion des ouverts $u$ tels que $(a\cap u) \subset b$.
    Passer de la logique intuitionniste à la logique classique revient à se restreindre aux ouverts qui sont l'intérieur de leur adhérence et ne pas s'occuper des autres.

    Autrement dit, à ne regarder que les $a$ tels que : $$ [ non(non(a)) ]= a $$
    Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
  • Maxtimax
    Maxtimax
    Je pense qu'avant de penser à des valeurs de vérité qui seraient des ouverts (même si c'est très instructif, et "il faut" le faire un jour), on peut essayer de s'abstraire totalement des valeurs de vérité.

    En fait, Mister Da, ta justification que les différentes formules sont équivalentes "par la table de vérité" utilise un théorème qui s'appelle "théorème de complétude", et qui n'est a priori pas trivial.
    Ce qui nous intéresse initialement devrait être la prouvabilité : est-ce que je peux prouver $p_i$ à partir de $p_j$ ($i,j\in \{1,2,3\}$)

    Comme le dit Christophe, il "suffit" des règles de prouvabilité intuitionnistes (en fait beaucoup moins) pour prouver $p_1\implies p_2$. Pour $p_3\implies p_1$ je n'ai jamais regardé en détails mais il est clair que l'intuitionnisme suffit aussi. C' est donc pour $p_2\implies p_3$, $p_1\implies p_3$ ou $p_2\implies p_1$ qu'il y a "un souci", et c'est là que quelque chose comme le principe du tiers exclu ou le raisonnement par l'absurde vont être nécessaires.

    Ensuite, il s'avère que si tu prends les règles intuitionnistes + le tiers exclu (donc que tu t'autorises la logique classique, celle de tous les jours en maths), tu as un théorème fabuleux qui est : "deux formules sont équivalentes (au sens qu'on peut prouver l'une à partir de l'autre en logique classique) si et seulement si elles ont même table de vérité". Et là on retombe sur nos pattes avec ce que tu dis au début sur leur équivalence.

    (après, pour rejoindre christophe, on peut énoncer et prouver un résultat similaire en logique intuitionniste, mais il faut une notion plus complexe de "table de vérité" puisqu'il faut regarder des espaces topologiques. Mais ça, c'est pour plus tard)
  • Mister Da
    Mister Da
    Bonjour,
    merci beaucoup à vous deux ! C'est beaucoup plus clair. Mais je découvre à chaque ligne de votre message l'étendue de mon ignorance ! Je n'avais pas réalisé qu'identifier des propositions qui ont la même table de vérité sous entendait un résultat loin d'être évident.

    Effectivement je n'avais pas précisé que je me place dans le cadre de la logique classique (avec tiers exclu ou sa variante du raisonnement par l'absurde) celle de tous les jours comme le dit Maxtimax.

    De manière très terre à terre, est-ce que je peux dire que le modus tollens et le modus ponens sont des règles primitives du raisonnement et que quand on se place dans le cadre de la logique classique (en admettant le principe du tiers exclu donc) ces règles semblent évidentes alors que dans le cadre d'autres logiques elles sont indispensables pour obtenir des raisonnements valides ?

    Je vais par simple curiosité creuser les ouverts d'espaces topologiques mais je pense pas avoir les reins assez solide pour l'heure en tant que logicien de dimanche de confinement.

    Encore merci pour votre aide.
    Cordialement,
    Mister Da
  • Foys
    Foys
    La sémantique des ouverts d'un espace topologique consiste en l'espèce (pour faire simple) à adopter les abréviations suivantes (empruntant leurs symboles à la logique), un espace topologique $(X,\tau)$ étant donné:

    Si $A,B \in \tau$, $A \vee B:= A \cup B$; $A \wedge B := A \cap B$.
    $A \Rightarrow B$ désigne l'intérieur de $(X \backslash A) \cup B$. On a notamment la propriété suivante:
    $A \Rightarrow B$ est le plus grand ouvert $V$ de $X$ tel que $A\wedge V$ ($=A \cap V$) est inclus dans $B$.
    $\perp := \emptyset$.
    $\neg Y := Y \Rightarrow \perp$ pour tout $Y\in \tau$.

    ***********
    Quantificateurs:
    Si $(A_i)_{i \in I}$ est une famille d'ouverts de $(X,\tau)$, $\exists i \in I, A_i$ désigne $ \bigcup_{i \in I} A_i$ et $\forall i\in I, A_i$ désigne l'intérieur de $\bigcap_{i \in I} A_i$.
    Ainsi $\exists i \in I, A_i$ et $\forall i\in I, A_i$ sont respectivement, dans l'ensemble ordonné par l'inclusion des ouverts de $(X,\tau)$, les bornes supérieure et inférieure de la famille $(A_i)_{i \in I}$.

    Lorsque la topologie de $X$ est discrète on a de plus pour tous $A,B,Y, (A_i)_{i \in I}$ ouverts:
    $A\Rightarrow B = (\neg A) \vee B$,
    $\neg Y=X\backslash Y$,
    $\neg(\forall i \in I, A_i) = \exists i \in I, \neg A_i$,
    $\neg (\neg Y) = Y$
    et $\neg (A \wedge B) = (\neg A) \vee \neg B$
    mais toutes ces égalités sont fausses dans un espace topologique plus général (le lecteur est invité à trouver des contre-exemples dans le simple cas de $\R$, à chaque fois ça se fait avec des intervalles bien sentis).
    Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
  • christophe c
    christophe c
    Mister Da a écrit:
    le modus tollens et le modus ponens sont des règles primitives du raisonnement et que quand on se place dans le cadre de la logique classique (en admettant le principe du tiers exclu donc) ces règles semblent évidentes alors que dans le cadre d'autres logiques elles sont indispensables pour obtenir des raisonnements valides ?

    Pour moi cette question n'a pas de sens. Une règle n'étant pas une affirmation, dire qu'elle est évidente ne se comprend pas.

    Le modus ponens remis sous forme d'affirmation est plus qu'évident puisqu'il dit:
    si si A alors B alors si A alors B

    Autrement dit, "si C alors C, en posant C:=(si A alors B)

    Mais si tu veux des informations: oui, le modus ponens est LA SEULE REGLE COMMUNE de déduction à toutes les logiques, sans exception. En un certain sens, on peut même dire que tout le reste est souvent mais surtout SE DOIT D'ETRE des axiomes et non des règles de déduction.

    Autrement dit, on préfère recenser sous la forme de l'axiome :

    $$A_1\to (A_2\to (\dot \to (A_n\to B) \dots )$$

    que sous la forme d'nue règle qui dit qu'une fois avoir prouvé $A_1,...,\dots A_n$, on a le droit de revendiquer avoir prouvé $B$.

    Parmi les exercices serpents de mer de ce thème, il y a qu'on peut prouver qu'on cette démarche est la bonne, donc qu'elle n'est pas une décision arbitraire.

    En règle générale, l'utilisation de "règles de déduction" plutôt que d'axiomes ne répond qu'à un seul besoin: les limitations pratiques du monde matériel.

    Il y a bien entendu des exceptions à ce paradigme, je t'ai simplifié les choses.

    Par ailleurs, la présence dans tes axiomes de:

    $(A\to B)\to ((X\to A)\to (X\to B))$
    $(A\to (B\to C))\to (B\to (A\to C))$

    d'une part et éventuellement de:

    $A\to (B\to A)$
    $(A\to (A\to B))\to (A\to B)$

    et même de

    $((A\to B)\to B)\to ((B\to A)\to A)$

    permet de rendre équiexpressifs l'usage avec règles et l'usage avec axiomes et modus ponens seul. (les 2 premier génèrent la logique linéaire, avec la 3ième tu as la logique affine, avec en plus le 4ième tu as l'intuitionniste et si tu prends les 5, tu obtiens la logique classique ($(X\to Y)\to Y$ est une manière de dire "X ou Y"))
    Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
  • christophe c
    christophe c
    Je vais googler "modus tollens" pour voir ce que tu entends par là.
    Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
  • christophe c
    christophe c
    Mouais, je viens de googler, mais je t'invite à oublier cette notion, sauf, dans ce cas dis le moi, si tu tiens très fortement à ce qu'on en débatte.

    En réalité, pour les logiques qui t'intéressent, elle ne fait qu'exprimer un cas particulier de la transitivité de implique, à savoir que de :

    A=>B et
    B=>Tout
    *
    tu peux déduire: A=>Tout

    ceci provenant du fait que $non(X)$ est une abréviation de ($X$ => Tout).
    Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
  • GaBuZoMeu
    GaBuZoMeu
    Moi, je suis fan du calcul des séquents. Et je viens de découvrir le paquet "bussproofs" de LaTeX qui permet d'écrire facilement les démonstrations - mais pas ici sur le forum.

    Une démonstration intuitionniste du fait que $P_3$ entraîne $P_1$ :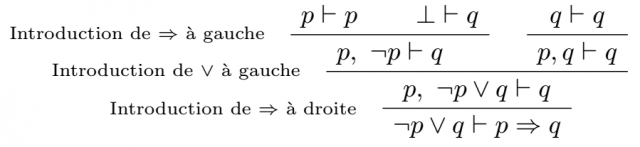

    200329032811218021.png

    Le code pour cette démonstration : 
    \begin{prooftree}
\def\labelSpacing{10pt}
\AxiomC{$p\vdash p$}
\AxiomC{$\bot\vdash q$}
\LeftLabel{\scriptsize Introduction de $\Rightarrow$ à gauche}
\BinaryInfC{$p,\ \neg p\vdash q$}
\AxiomC{$ q\vdash q$}
\UnaryInfC{$ p,q\vdash q $}
\LeftLabel{\scriptsize Introduction de $\vee$ à gauche}
\BinaryInfC{$p,\ \neg p \vee q \vdash q$}
\LeftLabel{\scriptsize Introduction de $\Rightarrow$ à droite}
\UnaryInfC{$\neg p \vee q \vdash p\Rightarrow q$}
\end{prooftree}
  • Mister Da
    Mister Da
    Bonjour,
    merci beaucoup pour vos explications.

    christophe c a mis le doigt où je coince au début de son dernier message.

    Quand on écrit "si si A alors B alors si A alors B" justement j'ai l'impression que le modus ponens dit si "C alors C" en posant C:=(si A alors B) et j'ai la sensation que ça enfonce une porte ouverte et c'est pour ça que je parlais d'évidence. En gros je n'ai pas l'impression de comprendre ce que dit le modus ponens puisque j'ai l'impression qu'il me dit : si c'est vrai...alors c'est vrai... et si c'est faux...bah alors c'est faux.

    Cordialement,
    Mister Da
Connectez-vous ou Inscrivez-vous pour répondre.

Bonjour!

Pour participer au forum, cliquer sur l'un des boutons :

Connexion S'inscrire

Catégories

In this Discussion

Qui est en ligne 8

CidrolinHéhéhéMister DaPaul-AC +4 Invités