Apprendre la logique (débutant)
Bonsoir,
Après avoir visionné cette vidéo : voir vidéo, je suis totalement perdu.
D'un côté, les cours classiques de logique ne distingue pas l'implication matérielle et l'implication habituellement employée. Par exemple dans un livre que je me suis procuré, un auteur commence à parler d'assemblage et créer les connecteurs logiques à partir de la négation et du "ou" :


Puis, il donne les axiomes de logique :

Et deux nouvelles règles :

Cela conduit naturellement aux tautologies :

J'ai l'impression qu'il y a plusieurs manière de traiter la logique classique. Ce cours je l'ai très bien compris. Peut-on raisonnablement voir l'implication (double barre) comme un connecteur comme dans l'extrait de cours ?
Après avoir visionné cette vidéo : voir vidéo, je suis totalement perdu.
D'un côté, les cours classiques de logique ne distingue pas l'implication matérielle et l'implication habituellement employée. Par exemple dans un livre que je me suis procuré, un auteur commence à parler d'assemblage et créer les connecteurs logiques à partir de la négation et du "ou" :


Puis, il donne les axiomes de logique :

Et deux nouvelles règles :

Cela conduit naturellement aux tautologies :

J'ai l'impression qu'il y a plusieurs manière de traiter la logique classique. Ce cours je l'ai très bien compris. Peut-on raisonnablement voir l'implication (double barre) comme un connecteur comme dans l'extrait de cours ?
Réponses
-
Que voudrais-tu que l'implication soit, si ce n'est un connecteur ?
-
Je peux comprendre que vous n'avez pas regardé la vidéo (elle dure trois heures). Alors regardez juste le court passage qui débute à 46 min 58. Il affirme selon lui que l'implication n'est pas un connecteur.
-
Bizarre :
J’y ai vu « connecteur $C_5$, « implique », et il dit bien que $\rightarrow$ connecte bien $A$ à $B$.
Je suis très novice également. -
Oui, mais quand il emploie la double barre il ne dit pas "implique" mais des mots comme "on déduit".
-
Ok c’est à partir de 48minutes du coup.
Je comprends mieux ta question. -
La distinction entre $\implies$ et $\to$ change de personne à personne, et même chez une personne d'un moment à l'autre. Il n'y en a pas un qui serait "le connecteur en logique du premier ordre" et l'autre qui sera "l'implication au sens usuel".
Je crois que c'est christophe qui disait (à raison) il y a autant de systèmes de logique du premier ordre qu'il y a de cours de logique du premier ordre. Chaque personne qui écrit un cours le fait à sa sauce avec ses envies du moment. La logique classique du premier ordre est très robuste donc des petites variations ne changeront pas le système qu'on obtient, à équivalence près.
Donc je ne sais pas répondre à ta question autrement que : oui, $\implies$ peut très bien être pris comme connecteur, mais $\to$ aussi, parfois les deux, parfois avec le même sens, parfois pas. ça dépend du cours que tu lis/suis. -
Merci Maxtimax, ça me rassure.
Je laisse tomber le cours de la vidéo et prendre celui de mon livre. Je souhaite faire de la logique simple, pas élaborée pour démontrer les théorèmes d'incomplétudes X:-( -
Je regarderai la minute 48 demain, car j'ai passé trop de temps sur des écrans et je vois flou. Mais globalement, les réponses qui t'ont été faites j'y adhère aussi. Quelle importance d'ailleurs, au fond, je n'ai pas rtop compris ce qui "ne serait pas un connecteur", ce serait quoi.
Je précise un peu: vouloir abréger Dem(A=>B) par un signe, par exemple A==>B mis entre A et B, me parait de toute façon peu pratique, même si c'est possible.
Il n'y a pas "d'implication matérielle" en maths, il y a "à la rigueur" l'implication prouvable (ie "ilest prouvé que A=>B"), et, mais pour des mauvaises raisons d'abus de langage, certaines tendances (heureusement peu présentes) à appeler implication matérielle le connecteur inclusion.
Bref, de toute façon en retenant que tu n'as à faire qu'à des connecteurs, tout ira bien.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Les théorèmes d'incomplétude ne nécessitent pas "d'apprendre la logique mathématique". Ils nécessitent de comprendre quelques philosophies simples sur la science. Je me mets à ta dispo dans les prochains jours si tu veux.
Ca ne t'interdit pas d'apprendre la logique bien évidemment. Mais je dirais que tu auras plus envie de l'apprendre APRES avoir ingéré les th d'incomplétude.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Je crois que c’est lié mais dites-moi si je sors du sujet :
On voit parfois des symboles qu’on traduirait comme « entraîne » mais c’est une sorte de T mis sur le côté comme :
$A \vdash B$. (Édit : merci Math Coss pour le symbole ;-))
Aussi, une espèce de trait de fraction qui se lit « sous les hypothèses $patati$ on déduit $patata$ ».
Édit : Un exemple $\begin{array}{rcl} A,C&\vdash& B\\ \hline C&\vdash &A\Rightarrow B\end{array}$
C’est encore des sortes de « implique ».
Mais c’est une histoire de « deuxième ordre », peut-être ? -
$\vdash$ (trouvé sur http://detexify.kirelabs.org/classify.html).
-
http://www.les-mathematiques.net/phorum/read.php?16,2118624,2119184#msg-2119184
@Dom:
Les symboles $\vdash$ et $\Rightarrow$ n'appartiennent pas au même niveau de discours.
En logique (vue comme étude du discours mathématique) il y a lieu de distinguer les énoncés formels (le discours mathématique en lui-même), des affirmations portant sur ces énoncés (le méta-discours).
1) $A \Rightarrow B$ est un énoncé mathématique lorsque $A,B$ sont des énoncés mathématiques.
2) $A_1,A_2...,A_n \vdash B$ est l'abréviation d'une affirmation (méta) portant sur des énonces mathématiques; cette affirmation étant: "B est démontrable à partir des énoncés $A_1,...,A_n$".Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
@Dom : j'ai lu aussi un cours avec ce genres de symboles, j'ai laissé tombé... 8-)
@Foys : oui dans la vidéo, la personne insistait beaucoup sur ça. Il parlait de la "logique employée" et de la "logique étudiée". Le fait de les mélanger conduisait à des paradoxes comme avec celui du menteur qui utilise dans la même phrase les deux niveaux de logique.
@Christophe : j'ai terminé de lire le cours de mon livre et j'ai plein de questions. Je commence à poser la première et quand tu passeras tu pourras m'aider ou une autre personne d'ailleurs qui s'y connait.
Question 1 : le premier axiome de logique (A1) dit que la relation (R ou R) ==> R est vraie. Avec les tables de vérité, j'ai trouvé pour cette relation que des "V". Je ne comprends pas où se trouve mon erreur de raisonnement.
Pourquoi la considérer comme vraie si je peux la justifier avec les tables ? Je dois certainement faire une très mauvaise interprétation des tables ou d'autre chose.
Question 2 : voilà une courte vidéo destiné à des MPSI sur l'implication : ICI. Le dernier commentaire désagréable de la vidéo est d'ailleurs l'auteur de l'autre vidéo (celle de 3 h sur la logique).
Mon œil certainement pas averti ne voit rien de problématique. Mais compte tenu du cours que j'ai, il doit y avoir surement un problème lol. -
Bonjour
"Peut-on raisonnablement voir l'implication (double barre) comme un connecteur comme dans l'extrait de cours ?"
Oui !
$(A\Rightarrow \Leftrightarrow (\bar A \vee
\Leftrightarrow (\bar A \vee  $
$
"Si tu avances, je tire." = "Avance pas ou je tire."
Tu peux transformer tes implications qui ressemblent à un mouvement, en expression logique figée. Donc oui, l'implication est un connecteur logique comme le "ou", le "et", le "non" (quoique le "non" soit unaire), l'équivalence, etc.Ce site est fatigant. Les gens modifient sans cesse leurs messages passés, et on ne comprend plus rien à la discussion. Je suis nostalgique du temps où, si on postait une bêtise, on devait l'assumer. Et si on cite le passage pour l'ancrer, l'administrateur supprime en disant qu'on n'a pas besoin de recopier le message passé. -
@PetitLutinMalicieux : d'accord. Mais n'es-tu pas en train de faire de l'interprétation ?
Je m'explique, l'assertion 3 + 1 = 4 ==> pi est un nombre irrationnel est vraie mais il y a pas de lien de cause à effet. Par rapport à ce qu'a dit Foys, j'ai l'impression qu'il faut distinguer la logique de la métalogique.
D'ailleurs pourquoi tu mets une équivalence est pas un symbole qui dit que c'est la même chose (une congruence avec les trois barres).
A l'aide ! X:-( -
Ton livre ressemble au livre Algèbre 1 de Gostiaux, la mise en page est la même, l'époque sûrement aussi. (Nostalgie de l'été après la spé avec une bière au bord de la plage...)
La démonstration des théorèmes d'incomplétude ne demande presque aucune base de logique. Par contre, comprendre ou juste voir une fois dans sa vie les 2 astuces principales devrait faire partie de la formation de tout mathématicien, c'est si joli.
Christophe te l'expliquera mieux que moi. (Il a un certain talent pour rendre les choses faciles à comprendre, je me rappelle de la preuve du théorème de Cantor-B en deux phrases, c'était magique). -
XV a écrit:Question 1 : le premier axiome de logique (A1) dit Avec les tables de vérité, j'ai trouvé pour cette relation que des "V". Je ne comprends pas où se trouve mon erreur de raisonnement.
Pourquoi la considérer comme vraie si je peux la justifier avec les tables ?
Je simplifie:
la règle du jeu de l'amont de tout ça est la suivante: on a un ensemble d'axiomes et une seule règle (je simplifie) qui dit qu'ayant prouvé A=>B et ayant prouvé A, on peut prétendre qu'on a prouvé B
Dans tout ça, les tables de vérité n'ont en quelque sorte "aucune importance". Enfin... si tu n'avais pas trouvé que des "vrai" ta situation serait pimentée, puique tu aurais un axiome et à côté, tu aurais un modèle (n'importe quelle ligne où tu trouves faux dans la TV) où il est faux.
Cette explication que je te donne peut être associée au couple de mots (syntaxe, sémantique) si tu veux googler.
Pour ta question2, faut que je regarde la vidéo que tu y évoques.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Pour ta question 2:Le dernier commentaire désagréable de la vidéo est d'ailleurs l'auteur de l'autre vidéo (celle de 3 h sur la logique).
Je n'ai pas regardé les 15mn, mais je n'ai pas trouvé de "commentaire"Mon œil certainement pas averti ne voit rien de problématique. Mais compte tenu du cours que j'ai, il doit y avoir surement un problème lol.
Euu, il y a plus qu'un problème. Cette vidéo est totalement foireuse à peu près du début à la fin (tout en tenant compte qu'il y a peut-être des parties pas à jeter dans ce que je n'ai pas vu.
- elle ne définit pas l'implication (elle dit "A=>B veut dire que si A alors, bin, vous comprenez, on a forcément B")
- elle confond implique avec alors
- elle ne traite pas de façon ferme => comme un connecteur
- elle noie tout dans du hors-sujet (des plages entières de temps consacrées à parler d'autre chose qui détournent l'attention sur l'implication
- elle présente réciproque et contraposée comme des sorte d'évangiles bizarre sans mention que tout le monde est déjà d'accord
En résumé, elle semble avoir été payée pour produire la plus mauvaise vidéo possible dans la limite qu'on ne s'aperçoive pas que c'est un gag. Elle ne semble d'ailleurs pas matheuse vus certains lapsus.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Bonjour Christophe.
D'accord.
Que veut concrètement dire "qu'ayant prouvé A=>B" ? Moi je le comprends comme "qu'ayant montré que A=>B est vraie". Est-ce la bonne interprétation ? C'est la règle du modus ponens ? -
J'en profite que je suis connecté pour t'expliquer l'incomplétude.
1/ Prérequis:
1.1/ Avoir bien compris la notion d'informatique théorique. Sa seule différence avec la pratique, c'est qu'il n'y a pas de limite finie pour la mémoire.
1.2/ Avoir "saisi dans tes tripes" lool que les preuves de maths sont une affaire de syntaxe. Dans la suite, on utilisera la convention que $x$ est vrai quand lancer la machine avec l'entrée $x$ produit un processus qui finit par s'arrêter.
2/ Soit $T$ la théorie dans laquelle tu décides de travailler.
3/ Soit $f$ la fonction à un argument qui quand on lui entre le $x$, se lance et s'arrête si et seulement si elle trouve une preuve (T-certifiée) de la phrase $non[x(x)]$.
4/ Tu lui donnes la phrase $f(f)$.
4.1/ Si ça ne s'arrête pas alors cette phrase est fausse, mais il n'y a pas de preuve que $non[f(f)]$
4.2/ Si ça s'arrête alors cette phrase est vraie, et comme ça s'est arrêté, il y a une preuve de $non[f(f)]$Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Oui à toutes tes questions du jour.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Et si tu veux savoir pourquoi on peut implémenter ça en arithmétique élémentaire (de Peano), c'est pour une raison qui n'a rien à voir avec la logique mathématique. Elle s'appelle "théorème chinois".
En gros ça te dit qu'il suffit d'avoir les nombres entiers pour parler de suites finies d'entiers, de haricots, de morceaux de raclettes, etc. Dit plus rigoureusement, dès lors que tu as implémenté les machins, tu as aussi implémenté les suites finis de machins.
De sorte que tu peux "raconter intégralement toute l'informatique théorique" dans l'arithmétique avec des $+; \times; \forall; =$.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Le théorème chinois (ici sous sa version efficace pour le contexte) te dit:
$(a,b,c,d) \mapsto $ la suite finie $u$ telle que $\forall n\leq d: u_n = $ le reste de $a+bn$ modulo $c$
est surjective de $\N$ sur l'ensemble des suites finies dont les termes sont des entiers.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Oulala, j'ai saisi quelques notions pour avoir déjà fait quelques recherches. Mais tu peux aussi utiliser des mots vraiment simples avec moi parce que j'ai un peu mal aux yeux avec les notations. A moins que tu as vraiment fait de la simplification.
Peux-tu donner un exemple simple de ce que tu expliques avec l'axiome des parallèles en géométrie ? -
@Xavier Var : je reprends les notations et la philosophie de Christophe.
Soit $T$ la théorie constituée des axiomes d'Euclide (que je ne connais pas par coeur).
Soit $A$ l'axiome des parallèles.
Tu fais tourner deux machines en même temps. A la première tu demandes une preuve $T$-certifiée de $A$. Idem pour la deuxième avec $non(A)$.
Et tu vas voir que tes deux machines vont boucler indéfiniment.
Bon, d'accord, il va te falloir vivre très très vieux pour t'en apercevoir, mais c'est un détail, et ça permet de comprendre l'indécidabilité de l'axiome des parallèles. -
Merci Martial c'est très clair ! (tu)
-
Ma troisième question.
Soient A et B deux assertions.
Je décide d'écrire A =(trois barres) B pour dire que A et B ont la même table de vérité.
Ainsi, A = A par exemple.
Je dispose aussi de non(A) ou B = A => B. Voilà ma question : étant donnés les assertions A et B, comment interpréter A <=> B par rapport à A = B ? -
Bonjour
$A\Leftrightarrow{}B\equiv{}(A\Rightarrow{}B)\wedge(B\Rightarrow{}A)\equiv\cdots$
Cordialement,
ThierryLe chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême). -
Ah. Je me suis mal expliqué. X:-(
Certaines personnes écrivent A = B quand d'autres écrivent A <=> B (un peu comme pour dire "c'est la même chose"). Je voulais savoir la différence subtile. -
À mon humble avis, tu raisonnes trop en terme de causalité. Ressemblance n'est pas corrélation et corrélation n'est pas causalité. Cela fait 3 niveau de liaison entre 2 propositions. Quand tu cherches la causalité dans l'implication, tu en demandes trop.
Quant à la différence entre les signes $\equiv$ et $\Leftrightarrow$, je pense que c'est équivalent. C'est juste pour éviter que tous les membres d'une égalité ne se mélange pas, et que l'on ne comprenne plus rien.
En latex, le signe de congruence est \equiv. Donc bon.Ce site est fatigant. Les gens modifient sans cesse leurs messages passés, et on ne comprend plus rien à la discussion. Je suis nostalgique du temps où, si on postait une bêtise, on devait l'assumer. Et si on cite le passage pour l'ancrer, l'administrateur supprime en disant qu'on n'a pas besoin de recopier le message passé. -
Comme d'habitude en maths, une expression désigne sa valeur.
Par contre, il y a un flou artisitique incorrect, mais pratiqué en ce qui concerne les phrases.
Si on adopte le point de vue rigoureux une phrase a deux valeurs possibles celles qui vivent dans $\{vrai; faux\}$. Dans ce cas,
$$(A=B)=(A\iff $$
$$
Par contre, si on est tenté de regarder une phrase comme la suite de signes qui la composent, l'égalité est matérielle (même suite de symboles), alors que $A\iff B$ continue de désigner l'égalité par valeurs.
Je te passe toutes les situations intermédiaires où par exemple, on va considérer que[le chien est beau] = [beau est le chien] = [(le) chien est (beau)] = etc
Mais "dans les petites classes", il vaut mieux, étant supposé acquis le signe "=>" (je l'abrège par $\to$ pour le latex) dire que:
$$(A\iff := ((A\to
:= ((A\to  \ et\ (B\to A))$$ Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
\ et\ (B\to A))$$ Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Merci Christophe ! J'ai bien saisi la différence (tu)
-
Bonjour,
Voici une tautologie de mon cours :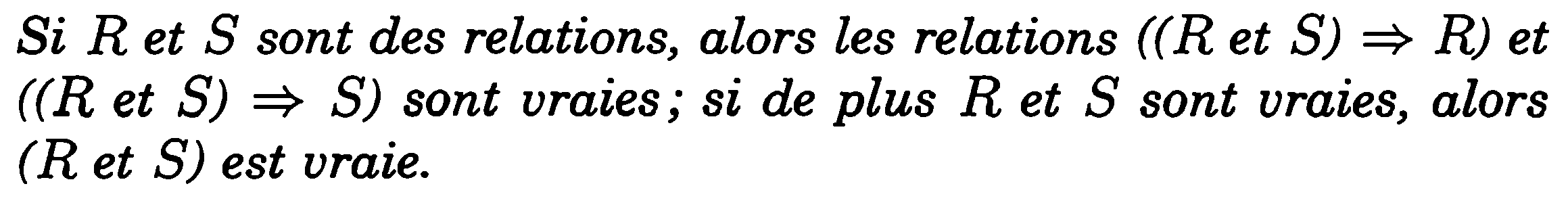
L'auteur affirme que cette dernière constitue la base du raisonnement par l'absurde. Peut-on m'expliquer ? -
Non c'est faux.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Ah. Quelle est la tautologie qui est associé à ce type de raisonnement ?
-
Ce n'est pas un raisonnement très formel.
L'équivalence
$$ [(A\ et\ \to C]\iff [A\to (B\to C)] $$
\to C]\iff [A\to (B\to C)] $$
que tu peux dire en français et "sans façon" :
[si A et B alors C] = [si A alors si B alors C]
est très en amont. Elle vaut dans toutes les logiques, y compris les plus faibles, donc pas seulement l'intuitionniste mais aussi les linéaires et affines. C'est "une adjonction" (mais ne regarde pas ce que veut dire adjonction, ça t'induirait en erreur ici)
Par ailleurs, dans les logiques faibles il y a 2 "et", mais elle ne vaut que pour un seul des deux, celui qui représente l'addition des ressources.
Comme la logique intuitionniste rend égales le fait d'additionner des ressources ou d'en prendre la borne supérieure, il y est valable que :
$$ [(inf(A,B)) \to C]\iff [A\to (B\to C)] $$
(C'est inversé, donc je préfère te le dire avec inf, plus un truc est petit plus il est vrai dans peu de mondes, d'où le inf à la place du sup pédagogique du dessus)
Bon tout ça, ça va peut-être te déconcerter. Retiens juste "autoritairement" de ma part que les logiques classiques et intuitionnistes donnent toutes deux la valeur "inf" à "et" et la valeur "sup" à "ou". Ca n'a rien à voir avec le RPA, qui lui, ajouté à la logique intuitionniste, donne la logique classique.
Parler de tautologie ne sert à rien, car toutes les théorèmes (y compris ceux prouvables seulement à l'aide du RPA) sont des tautologies. Quand un truc n'est pas une tautologie, il n'est tout bêtement pas un théorème de maths, même fortes.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Merci pour ces précisions.
La seconde partie de ton message est plus délicat.
L'équivalence que tu as donnée (la première) c'est elle qui constitue la base du RPA ? Je n'arrive pas à faire le lien avec la pratique, c'est à dire le fait de nier l'hypothèse pour aboutir à une contradiction. -
Demain je te ferai un topo complet et simpleAide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Dans mon message, je ne t'ai parlé de RPA QUE pour te dire qu'il n'était pas évoqué.
(1) Tu as plusieurs logiques célèbres . La plus faible est la linéaire et la plus forte est la classique.
(2)Ces notions de logiques sont syntaxiques, c'est à dire qu'on parle de règles du jeu de preuves (comment reconnaitre un texte qui est une preuve d'un texte qui ne l'est pas, un texte étant une suite de suites de signes)
(3) Par ailleurs, tu as ce qu'on appelle "la sémantique" (qui s'occupe des "modèles des phrases"). Selon la logique que tu as envie d'utiliser les sémantiques sont différentes.
(4) Tes "très chères" tables de vérité sont tout bêtement des tableaux qui permettent de lister TOUS LES MODELES d'un coup d'une phrase dans le contexte où tu utilises LA LOGIQUE CLASSIQUE. Donc retisn bien qu'avec des TV, tu ne fais que de la logique claissique et le RPA est embouteillé dedans sans même que tu aies quelque chose à faire
(5) Les liens entre syntaxe et sémantique sont donnés par des théorèmes dits de complétude.
(6) Par exemple, pour la logique classique, il dit que si toutes les cases de ta phrase dans la TV sont labellisées vraies alors il existe une preuve en logique classique de ta phrase.
(7) je répète donc : si tu veux me poser des questions sur le RPA, ne me parle surtout pas de TV puisque ça n'a rien à voir: (a) c'est de la sémantique et (b) qui ne concerne que la logique classique.
(8) Le RPA est un AXIOME qui permet, quand il est ajouté à la logique INTUITIONNISTE d'obtenir la LOGIQUE CLASSIQUE. Autrement dit, pour toute phrase $P$ :P est un théorème classique si et seulement si RPA=>P est un théorème intuitionniste
(9) A partir de ces précisions, relis ta question, relis ma réponse, et redemande-moi ce que tu veux.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Précise moi ton niveau et une de tes spécialité et je te traduirai la logique dans cette spécialité. C'est probablement le plus simple de faire comme ça.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
D'accord.
Mon niveau en math est Terminale, Poste-bac et je n'ai pas vraiment de spécialité.
Je reprends chacune de tes phrases.
1) La logique intuitionniste fait partie de la liste ? Il y en a combien ?
2) Ok. Si j'ai bien compris, on n'a aucun recul sur la véracité d'une assertion que si on l'admet vraie où bien qu'une règle l'affirme ?
3) 4) 5) Ok.
6) Bien vu.
7) 8) 9) Le RPA est un axiome de quel logique ? Et que dit-il ? -
@Xavier Var : bonjour. Il y a notamment les logiques minimale, intuitionniste, modale, classique. Tu ferais bien d'acquérir le livre de Jacques Duparc, livre intitulé "la logique, pas à pas". Presque tout y est, ou du moins tout ce dont tu as besoin de savoir dans l'immédiat.Le chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême).
-
Bon, effectivement ... J'essaie de te décrire les choses :
1/ Définition: un texte est une suite finie de phrases
2/ Tout texte est une preuve
3/ Extraction des hypothèses d'une preuve :
3.1/ La première phrase du texte est obligatoirement une hypothèse
3.2/ Quand tu passes d'une phrase X à la suivante Y dans ton texte, tu dois admettre que (X=>Y) est une hypothèse, ou si tu veux tu as le droit de dire que Y est une hypothèse et que tu ne l'as pas inféré de la phrase précédente.
4/ C'est la dernière phrase du texte que l'on considère comme prouvée à partir des hypothèses du texte.
5/ Un axiome est une hypothèse parmi d'autres dans un texte.
6/ Définition: une phrase P est dite prouvable dans une théorie T quand il existe au moins une preuve de P dont toutes les hypothèses sont dans T
Par exemple: $C$ est prouvable dans la théorie $\{A; A\to B; B\to A; B\to C\}$. Je te laisse trouver une preuve.
7/ Remarque: tu n'as donc pas besoin de "donc", puisqu'il est tacite d'une phrase à la suivante.
8/ Tout ceci est très théorique et non utilisable en pratique car trop long, je te donne juste de quoi comprendre à fond les principes!!
9/ Exemple de preuve:
a
b=>(a et b)
a et b
a et b et c
Avec cette preuve, tu as prouvé (a et b et c)
en supposant:
a
a =>(b=>(a et b))
(b=>(a et b))=>(a et b)
(a et b)=>(a et b et c)
10/ Tu remarqueras que dans ta preuve il y a des axiomes "plus cool" que d'autres, ou pour être plus précis "plus incontestable" que d'autres. Je les numérote :
a (1)
a =>(b=>(a et b)) (2)
(b=>(a et b))=>(a et b) (3)
(a et b)=>(a et b et c) (4)
Les 1,3,4 paraissent gratuits, alors que le (2) parait incontestable. (Je le réécris: si a alors si b alors [a et b] )
11/ Certaines hypothèses s'appellent des "axiomes logiques". C'est quand le crédit qu'on leur accorde est INDEPENDANT des sens des mots qui composent lesdites hypothèses.
12/ En gros, voilà le principe.
13/ Bon ça, ce n'était qu'un exemple "un peu simplifié.
14/ Pour être un tout petit peu moins simple, en fait, on ne regarde pas "la ligne précédente", car c'est "trop chiant et contraignant". On regarde n'importe quelle ligne strictement avant. Et on ajoute "car" à droite. De plus, on peut ne pas mettre le mot "car". DE PLUS: tu as le droit de remonter DEUX lignes avant. Ca donne la règle d'extraction:
X
Y
Z
axiome extrait de ce passage : X=>(Y=>Z)
15/ Selon ce nouveau format, voici une preuve:
a
b
b=>(a et b) (car a)
a et b (car b)
Les hypothèses (tu peux aussi dire "les admis") sont :
a
b
a => (b=> (a et b)) <---- ici, important, j'ai utilisé le car, je n'ai pas pris la ligne d'avant
b=>((b=>(a et b))=>(a et b))
Cette preuve est déjà plus intéressante car regarde comme les axiomes sont finalement "pas très affirmatifs" alors que la conclusion est "assez impressionnante".
16/ Suivant les différents formats que tu utilises tu as des règles d'extraction d'hypothèses de sorte que tout texte est une preuve de sa dernière phrase à partir des hypothèses qu'elle fait, et la façon d'extraire les hypothèses qu'elle fait a été au fil du temps peufiné sans tricher de manière à avoir "de nos jours" quelques chose d'assez pur et concis. (Mais même les meilleurs versions trouvées sont longues, t'inquiète, tu n'as pas besoin d'être frustré.
17/ Maintenant regarde les deux preuves suivantes, comparées:
a
a=>b
b
dont les axiomes sont
a
a=>b
a=>((a=>b)=>b)
j'imagine qu'en tant que débutant, tu trouves ça "matrixant".
Maintenant regarde la preuve suivante:
a=>b
a
b
Les axiomes sont :
a=>b
a
(a=>b)=>(a=>b)
A part le troisième hypothèse, les 2 premiers sont les mêmes, et la conclusion est la même. On a donc une meilleure preuve car le troisième axiome de la deuxième semble plus incontestable que le troisième de la première.
18/ Voilà, voilà. Note bien que la seule règle du jeu intangible est "tout ce que je suppose doit se voir". C'est ce qui fait l'honnêteté scientifique (qui l'oppose aux religions et aux textes politiques) et surtout ce qu'on appelle "le côté formalisé" de la science et des maths (tout se voit, pas d'interprétation possible ambigue)
19/ Maintenant tu as des axiomes qu'on utilise CONTINUELLEMENT: exemple.
a=>(b=>c)
(a et b)=>c
(b et a)=>c
b=>(a=>c)
Dans cette preuve, en partant du seul admis gratuit a=>(b=>c)
je suis arrivé à la conclusion b=>(a=>c)
à l'aide d'axiomes que personne n'aurait l'idée de contester.
20/ Je te liste maintenant, en plusieurs groupes, les axiomes "que personne n'aurait l'idée de contester".
20.1/ Groupe 1 (pur reformulation verbale) :
a=>a
(a et b) => (b et a)
(a=>(b=>c)) => ((a et b)=>c)
((a et b)=>c) => (a=>(b=>c))
20.2/ Groupe 2 (transitivité)
( (a=>b) et (b=>c) ) => (a=>c)
20.3/ Groupe "existence de poubelles à volonté"
(a et b)=> a (ie tu peux jeter b)
20.4/ Clonabilité des hypothèses (groupe 3)
a=> (a et a)
21/ Et bien tout ça, ça ne te donne que la logique intuitionniste!!! (tu me diras, c'est normal, c'est tellement des platitudes tout ça)
22/ Il y a un axiome (enfin plusieurs versions, toutes équivalentes) dit du "raisonnement par l'absurde" qui affirme EN PLUS de ce qui précède une chose qui est importante et qui permet d'avoir l'équivalence entre la logique et les tables de vérité. C'est (par exemple):(((a=>b) => c) et (a=>c) ) => c
Philosophiquement, cet axiome (qui parait très fort) te dit en gros que si tu as (x=>y)=>z alors tu as (x ou z). Arutement dit que si tu es capable de garantir qu'en te servant du cadeau qu'on te ferait qui serait l'implication (x=>y) tu pourrais l'utiliser comme garantie de z, alors c'est forcément que tu as déjà z en quelque sorte, ou à tout le moins que pour l'obtenir et te servir la garantie, tu vas devoir lui fournir x (afin de chopper y en retour).
Dit comme ça, ça parait évident, après avoir pourtant un premier temps lu l'axiome comme une affirmation bien plus gratuite que les précédents.
Le fait est que comme ça exige une psychanalyse (un back-retour sur la garantie), on ne peut pas prouver cet axiome dit "du raisonnement par l'absurde" à l'aide des autres axiomes.
Bon digère TRANQUILLEMENT ce début, etr reviens avec des questions.
Je te parlerai du "ou" après.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
@titi: tout ça c'est une même logique qui est essentiellement l'intuitionniste. Mais en fait, il "sort du bac", donc vaut mieux qu'il suive une enfilade de posts en posant ses propres questions après, je le dirigerai vers des sources livresques. Mais il semble utile de diagnostiquer d'abord ses réactions. Comme tu sais, le lycée s'est écroulée et les sciences n'y sont plus du tout distinguées en termes d'exposés, des religions. Il est donc utile qu'il identifie les exigence de déductif. Sinon, même un manuel de logique serait lu comme un exposés de dogmes.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
@XV: il faut bien comprendre que tu as deux situations humaines:
1/ acquérir une compétence en logique APRES avoir fait pas mal de "vraies maths".
2/ acquérir une compétence en logique AVANT avoir fait des "vraies maths".
qui sont très différentes. Ce matin, tu nous apprends que tu es dans la situation 2, à savoir que tu n'as jamais de maths, en dehors du fait que tu sais que les maths, c'est une pratique où on écrit des signes bizarres sur du papier et qu'au moindre changement de signe, tout peut se crasher.
C'est pourquoi, je te recommande de lire doucement ce que j'ai écrit et de ne PAS FORCER. A ton stade, pas besoin de te concerntrer ou faire des exos, juste besoin de méditer (c'est un peu le contraire de la concentration) sur le fait qu'en math, on ne fait que bilanter ce qui est évident.
Le miracle à qu'à "bilanter" des truismes, on a fini par construire des avions à réaction et des ordinateurs ultrapuissants. Mais ce "miracle", tu ne vas pas le "capter" demain. Le risque quand on va trop vite, c'est de retomber dans la religion et se mettre à raconter n'importe quoi par "indigestion face au vide".
Exemple de preuve de maths:
a
a
a
J'ai supposé pas seulement a. J'ai aussi utilisé l'axiome a=>a, et l'axiome a=>a, une DEUXIEME fois par exemple.
Et ma conclusion est a.
Ces phénomènes qui ont l'air COMPLETEMENT RIDICULES sont en fait de TOUTE PREMIERE IMPORTANCE en science puisqu'on ne se donne le droit qu'à CES TRUISMES. Tout le reste est considéré comme supposé et est donc ATTAQUE par les raisonnements scientifiques (et non pas défendu).
Voilà pourquoi, je te recommande de digérer doucement cette prise de conscience.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
@Thierry Poma : je l'ai mis en favoris, merci ! Je crois vraiment avoir besoin d'un VRAI ouvrage sur la logique (hors scolaire).
@Christophe : très agréable à lire et cela m'a donné envie de faire le petit exercice. La logique me semble "froid" en fait, dépourvue de toute émotions X:-(.
Je vais relire attentivement ton long message et de poser les questions ensuite.
Petite question : la logique est-elle considéré comme un domaine des maths au même titre que l'analyse ? Certains mathématiciens, comme Euler ont touchés à tous les domaines sauf la logique. -
Je te donne un exemple d'une autre preuve intéressante:
(a=>b)=>(a=>b)
((a=>b) et a) =>b
(a et (a=>b))=>b
a=>((a=>b)=>b)
et bien, je ne détaille pas, mais cette "simple preuve" toute bête est à l'origine de quasiment toutes les grandes découvertes récentes*** en maths. Tu vois qu'il faut adapter "sa mentalité" à l'activité que constitue faire des maths. Sinon, on fonde dans le HS.
[small]*** le plongement naturel $$(x\mapsto (f\mapsto f(x)))$$
est présent dans quasiment tous les articles de recherches fondamentales[/small]Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Petite question : la logique est-elle considérée ...
En fait, ce sont les maths qui sont un domaine de la logique (les maths sont de la logique appliquée aux choses concrètes). Mais comme c'est réflexif, en retour la logique est aussi un domaine des maths et les logiciens taffent dans les labos financés par les maths.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Je m'attaque uniquement à tes écrits de 1/ à 4/ pour l'instant.
Un texte est une suite finie de phrases.
Est-ce que je peux, pour illustrer, prendre des exemples de type mathématiques ? Par exemple, dire : 8 est un nombre impair. Est-ce bien un texte vis-à-vis de la définition ? -
Oui. bien sûr. C'est un texte d'une ligne :-D
J'ai fait exprès de dire "texte". La deuxième ligne est l'élément $u_2$ de la suite par exemple (si on commence à 1 et pas à 0)Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres






