Fonction transfert à partir de l'équa.diff
Bonjour à tout le monde,
ma question consiste à trouver l'expression de la fonction de transfert d'un correcteur PD à partir de l'équation différentielle de sa sortie.
Voici l'énoncé global :
On veut maintenir à la verticale une fusée pendant la phase atmosphérique de sa trajectoire.
Pour ce faire, on fait pivoter la tuyère du moteur principal suivant deux axes. En première approximation, les dynamiques de chacun des deux axes sont à peu près découplées, et l’on peut donc les modéliser séparément. On s’intéresse ici à l’un de ces deux axes d’évolution. La variable de sortie $y$ est l’angle d’inclinaison du lanceur et la variable de commande $u$ l’angle de braquage de la tuyère dans ce plan. Le temps (mesuré en secondes) est noté $t$ . Quand $u$ et $y$ restent tous les deux proches de $0$, un modèle simplifié du comportement du système est donné par l’équation différentielle : $$
\frac{d^2y(t)}{dt^2}-4y(t)=2u(t)+v(t)
$$ où $v(t)$ est une perturbation qui correspond principalement à l'effet du vent.
(Après il y à des questions auxquels j'ai répondues)
Voici l'énoncé concernant ma question:
On utilise pour commander le système un régulateur proportionnel-dérivé $PD$ de la forme : $$
u(t) = -k\Big( y(t)-\alpha y_r(t)+T_D \frac{dy(t)}{dt} \Big)
$$ où $k>0,\ T_D>0,\ \alpha>0$ sont trois constantes, et où $y_r(t)$ est une consigne d’inclinaison. L’objectif de commande est alors d’annuler l’erreur de poursuite :
Voici ma démarche :
J'utilise la transformé de Laplace pour passer le signal en domaine fréquentiel :
et donc : $C(p)=\dfrac{U(p)}{e(p)}=\dfrac{-K(Y(p)-\alpha Y_r (p)+T_DpY(p))}{Y(p)-Y_r(p)} $
cette forme du $C(p)$ je ne suis pas sûr qu'elle convienne...
Concernant le schéma bloc, je le déduis à partir de l'expression de $U(p)$ :
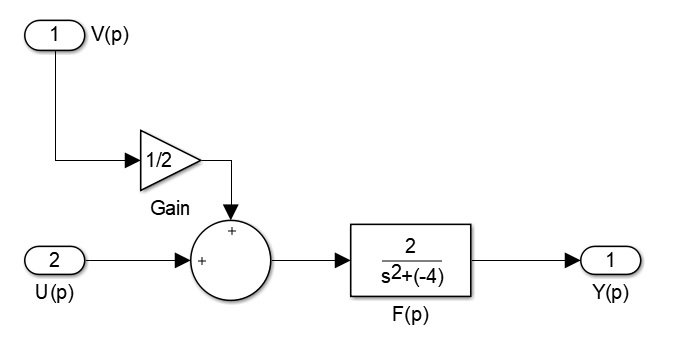
et voici le schéma bloc demandé :
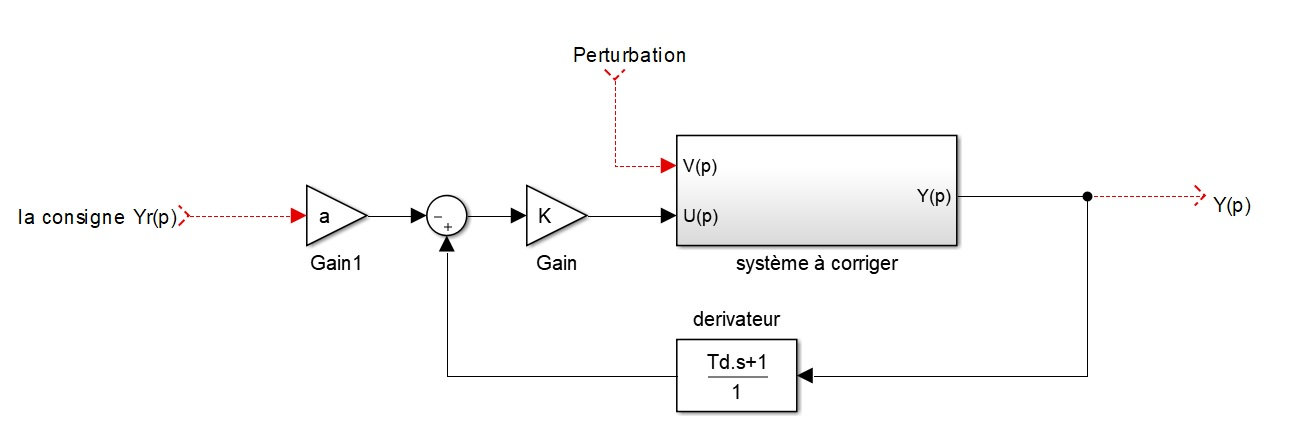
Pourriez-vous me donner votre avis, car je ne suis pas vraiment sûr de ma démarche et surtout la fonction de transfert du $C(p)$ devrait, il me semble, être plus simple et ne pas contenir les $Y(p)$ et $Y_r(p)$.
Merci par avance.
PS: il n'y a pas vraiment des forums en automatique à l'équivalence de celui-ci en mathématiques, mais si vous en connaissez ça m’intéresse.
ma question consiste à trouver l'expression de la fonction de transfert d'un correcteur PD à partir de l'équation différentielle de sa sortie.
Voici l'énoncé global :
On veut maintenir à la verticale une fusée pendant la phase atmosphérique de sa trajectoire.
Pour ce faire, on fait pivoter la tuyère du moteur principal suivant deux axes. En première approximation, les dynamiques de chacun des deux axes sont à peu près découplées, et l’on peut donc les modéliser séparément. On s’intéresse ici à l’un de ces deux axes d’évolution. La variable de sortie $y$ est l’angle d’inclinaison du lanceur et la variable de commande $u$ l’angle de braquage de la tuyère dans ce plan. Le temps (mesuré en secondes) est noté $t$ . Quand $u$ et $y$ restent tous les deux proches de $0$, un modèle simplifié du comportement du système est donné par l’équation différentielle : $$
\frac{d^2y(t)}{dt^2}-4y(t)=2u(t)+v(t)
$$ où $v(t)$ est une perturbation qui correspond principalement à l'effet du vent.
(Après il y à des questions auxquels j'ai répondues)
Voici l'énoncé concernant ma question:
On utilise pour commander le système un régulateur proportionnel-dérivé $PD$ de la forme : $$
u(t) = -k\Big( y(t)-\alpha y_r(t)+T_D \frac{dy(t)}{dt} \Big)
$$ où $k>0,\ T_D>0,\ \alpha>0$ sont trois constantes, et où $y_r(t)$ est une consigne d’inclinaison. L’objectif de commande est alors d’annuler l’erreur de poursuite :
$e_P(t)=y(t)-y_r(t)$
1/ Déterminer la fonction de transfert du régulateur $C(p)$ et la fonction de transfert de la chaîne directe $T(p)$ (fonction de transfert de boucle) de cet asservissement. Montrer qu’en prenant $r(t)=\alpha y_r(t)$, le système asservi peut se mettre sous une forme standard, et dessiner un schéma-bloc du système asservi.Voici ma démarche :
J'utilise la transformé de Laplace pour passer le signal en domaine fréquentiel :
$ U(p)=-K(Y(p)-\alpha Y_r (p)+T_DpY(p)) $
Je sais que : $e(p)C(p)=U(p)$ alors $C(p)=\dfrac{U(p)}{e(p)}=\dfrac{-K(Y(p)-\alpha Y_r (p)+T_DpY(p))}{Y(p)-Y_r(p)} $et donc : $C(p)=\dfrac{U(p)}{e(p)}=\dfrac{-K(Y(p)-\alpha Y_r (p)+T_DpY(p))}{Y(p)-Y_r(p)} $
cette forme du $C(p)$ je ne suis pas sûr qu'elle convienne...
Concernant le schéma bloc, je le déduis à partir de l'expression de $U(p)$ :
$U(p)=\big(\alpha Y_r(p)-Y(p)(1+T_D p)\big)K$
Ici d'abord le système à corriger :
et voici le schéma bloc demandé :

Pourriez-vous me donner votre avis, car je ne suis pas vraiment sûr de ma démarche et surtout la fonction de transfert du $C(p)$ devrait, il me semble, être plus simple et ne pas contenir les $Y(p)$ et $Y_r(p)$.
Merci par avance.
PS: il n'y a pas vraiment des forums en automatique à l'équivalence de celui-ci en mathématiques, mais si vous en connaissez ça m’intéresse.
Réponses
-
Bonjour,
effectivement la forme que tu trouves ne convient pas puisque ce n'est pas une fonction de transfert. La forme que tu dois obtenir doit être de la forme suivante : $$
C(p)=\frac{b_0+b_1p+\cdots+b_mp^m}{1+a_1p+\cdots +a_np^n}
$$ avec $b_0,\dots,b_m,a_1,\dots,a_n$ des réels. À mon avis (il faudrait voir ton cours) tu dois plutôt chercher la fonction de transfert entre les signaux $e(t)=r(t)-y(t)$ et $u(t)$ (sinon pourquoi considérer $r(t)=\alpha y_r(t)$ ?). De plus, tu ne précises pas, mais est-ce que $y_r$ est constant ? Parce que sinon je ne vois pas comment tu obtiens la dernière égalité. Il faudrait également savoir quelle est cette forme standard dont parle la question (parce que les formes standards varient d'un livre à l'autre).
Cordialement.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres