anneau dodécaèdre
dans Algèbre
Bonjour,
Peut-être à chaque solide de Platon on peut associer un anneau dont les éléments seraient les k-faces (faces de dimension k) avec un ordre tel qu'il fasse de l'anneau le poset correspondant au solide ( une face est plus petite qu'une autre si elle la contient)
Et de plus que l'addition soit compatible avec les rotations du solide (je sais pas encore trop dans quel sens)
Pour le tétraèdre c'est l'anneau de Boole, l'ordre c'est $x\leq y$ ssi $x=xy$, pour le cube et l'octaèdre c'est les 3-anneaux ( les anneaux qui vérifient $3x=0$ et $x^3=x$, quand ils sont finis c'est $Z/3Z^n$), on met 0 au milieu par exemple le carré :
(1,2)----(0,2)----(2,2)
(1,0)----(0,0)----(2,0)
(1,1)----(0,1)----(2,1)
(2,0) est l'arête qui relie les sommets (2,2) et (2,1)
l'ordre de l'octaèdre c'est $x\leq y$ ssi $x=x^2y$, pour le cube c'est l'ordre dual
Le simplexe, l'hypercube et l'hyperoctaèdre existent pour toute dimension, mais pas le dodécaèdre donc ça doit être un anneau particulier.
L'anneau doit avoir 62 éléments au moins ( nb de faces+nb d'arêtes+nb de sommets), mais je crois qu'il doit avoir un élément au milieu (qui serait le neutre pour l'addition) donc ça ferais 63 éléments.
Si j'ai bien compris le groupe additif serait $Z/3Z^2\times Z/7Z$ ou bien $Z/63Z$
L'opposé d'un élément est obligatoirement la k-face opposée par argument de stabilité par rotation.
L'addition de deux faces qui se touchent en une arête est nécessairement soit l'arête commune soit sont opposée, on peut dire aussi d'autres choses, peut-être par associativité on peut déduire l'addition pour tout élément de l'anneau.
Connaitriez-vous un programme qui puisse faire cela?
Qu'en pensez-vous?
Peut-être à chaque solide de Platon on peut associer un anneau dont les éléments seraient les k-faces (faces de dimension k) avec un ordre tel qu'il fasse de l'anneau le poset correspondant au solide ( une face est plus petite qu'une autre si elle la contient)
Et de plus que l'addition soit compatible avec les rotations du solide (je sais pas encore trop dans quel sens)
Pour le tétraèdre c'est l'anneau de Boole, l'ordre c'est $x\leq y$ ssi $x=xy$, pour le cube et l'octaèdre c'est les 3-anneaux ( les anneaux qui vérifient $3x=0$ et $x^3=x$, quand ils sont finis c'est $Z/3Z^n$), on met 0 au milieu par exemple le carré :
(1,2)----(0,2)----(2,2)
(1,0)----(0,0)----(2,0)
(1,1)----(0,1)----(2,1)
(2,0) est l'arête qui relie les sommets (2,2) et (2,1)
l'ordre de l'octaèdre c'est $x\leq y$ ssi $x=x^2y$, pour le cube c'est l'ordre dual
Le simplexe, l'hypercube et l'hyperoctaèdre existent pour toute dimension, mais pas le dodécaèdre donc ça doit être un anneau particulier.
L'anneau doit avoir 62 éléments au moins ( nb de faces+nb d'arêtes+nb de sommets), mais je crois qu'il doit avoir un élément au milieu (qui serait le neutre pour l'addition) donc ça ferais 63 éléments.
Si j'ai bien compris le groupe additif serait $Z/3Z^2\times Z/7Z$ ou bien $Z/63Z$
L'opposé d'un élément est obligatoirement la k-face opposée par argument de stabilité par rotation.
L'addition de deux faces qui se touchent en une arête est nécessairement soit l'arête commune soit sont opposée, on peut dire aussi d'autres choses, peut-être par associativité on peut déduire l'addition pour tout élément de l'anneau.
Connaitriez-vous un programme qui puisse faire cela?
Qu'en pensez-vous?
Réponses
-
Je crains que tu aies réinventé l'eau chaude. ;-)
http://fr.wikipedia.org/wiki/Complexe_simplicial -
Merci de votre réponse mais je ne vois pas d'anneau dans l'article wikipédia?
-
On prend l'anneau qu'on veut (je ne connais pas assez en détail la théorie pour savoir l'intérêt de prendre n'importe quel anneau, j'ai seulement rencontré l'utilisation de $\mathbb{Z}$ ou de $\mathbb{Z}/2\mathbb{Z}$) et on considère des combinaisons linéaires formelles (des complexes de p-simplexes sauf erreur) $\sum_{k=0}^{n} a_k.S_k$ où $a_k$ est un élément de l'anneau considéré et $S_k$ des simplexes (dans le cas d'une surface, ce sont des triangles orientés). . Après on déroule une machinerie qui conduit à l'homologie simpliciale.
Ce sont des reminescences d'un vieux cours de topologie algébrique et j'espère que ce que j'écris n'est pas trop faux. B-)- -
Si je comprend bien, ce que tu dis s'applique au simplexe, et aux autres si on les découpes en simplexes, mais comment multiplier deux simplexes?
-
Salut,
L'objet le plus proche de ce que tu proposes, comme l'a dit FDP, c'est l'homologie (à coefficients dans un anneau $\mathbb A$ quelconque, par exemple $\mathbb Z$).
Si tu veux une structure multiplicative, il faut considérer plutôt la cohomologie : c'est un anneau gradué (les éléments commutent ou anti-commutent suivant leur degré). Le produit dans cet anneau ressemble un peu à ce que tu as dit au début : c'est donné par l'intersection.
Sinon l'autre objet algébrique que j'ai envie d'associer à un polytope de $\mathbb R^n$, c'est : je prends$G$ le groupe d'isométries, je prends un anneau $\mathbb A$ (par exemple $\mathbb Z$), et je regarde l'algèbre du groupe, notée $\mathbb A[G]$ : c'est un anneau, muni d'une structure de $\mathbb A$-algèbre, non commutatif si $G$ n'est pas commutatif. Mais toi tu as plutôt l'air de penser à la cohomologie. -
Je crois que vous n'avez pas bien compris le problème.
Il s'agit de trouver un anneau dont les éléments sont les k-faces (faces de dimension k) donc d'ordre 63 (on compte le solide tout entier comme pour le cube)
Si on dit que l'addition c'est $Z/3Z^2\times Z/7Z$ on peut peut-être dire que les 8 éléments d'ordre 3 sont les sommets du cube inscrit, et que les 6 éléments d'ordre 7 sont les arêtes qui sont en face des faces du cube inscrit.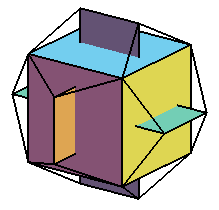
Qu'en pensez-vous ? -
Avec ton dernier message, en effet, je n'ai strictement rien compris.
Si tu es dans une demande de réponse, il va te falloir être précis car cela me semble bien flou tout ceci. -
On a compris le problème. :-)
C'est juste que la réponse n'est pas exactement celle que tu penses, et qu'il faut un peu changer la formulation du problème et la construction de ton objet pour que ça prenne du sens et "marche" correctement. :-)
Par ailleurs : parler "du" cube inscrit n'a pas de sens : dans un dodécaèdre, tout sommet est le sommet d'un cube inscrit (et même de plusieurs cubes inscrits il semble : deux je dirais). Ton dessin peut donner l'impression qu'il n'y a qu'un cube, mais c'est juste que les autres ne sont pas dessinés (et si on dessine simultanément les cinq cubes, on ne voit plus rien ou presque).
Si tu veux absolument t'entêter à "associer" $\mathbb Z/7\mathbb Z \times (\mathbb Z/3\mathbb Z)^2$ au dodécaèdre, tu peux, mais par contre, arrives-tu à donner une description raisonnable de la somme ? du produit ? Que signifie géométriquement le fait pour certains éléments d'être d'ordre sept ?
Pour te convaincre que cette approche ne donnera pas grand chose: fais la même chose avec le tétraèdre : quatre faces, six arêtes, quatre sommets, plus un élément comme tu dis pour l'élément neutre, ça fait 15.
Comme disait Desproges : est-ce bien raisonnable ? -
J'essaye de mettre sur l'ensemble constitué des faces, des arêtes et des sommets (+1 ou 2 éléments) d'un solide de Platon une structure d'anneau avec un ordre qui s'exprime avec la multiplication, et que cet ordre soit celui du polyèdre concerné (une i-face est plus petite qu'une j-face si la i-face est contenue dan la j-face).
Pour le tétraèdre, c'est $\mathbb{F}_2^4$ l'odre c'est $x\leq y$ ssi $x=xy$,
pour le cube et l'octaèdre c'est $\mathbb{F}_3^3$, l'ordre pour l'octaèdre c'est $x\leq y$ ssi $x=x^2y$ et pour le cube c'est le dual de cet ordre.
Les solides duaux l'un de l'autre ont même anneau c'est juste que l'ordre est dual l'un de l'autre
On cherche l'anneau du dodécaèdre (et on aura du même coup celui de l'icosaèdre), un dodécaèdre a 20 sommets, 30 arêtes et 12 faces
En tout cela fait 62, mais on rajoute le solide tout entier comme pour le cube, on doit donc chercher un anneau à 63 éléments
Je crois aussi que l'addition doit être compatible avec la symétrie centrale de centre le milieu du dodécaèdre, c'est à dire que que faire l'opération puis faire la symétrie c'est pareil que faire la symétrie puis faire l'opération
Je dis ça parce que je pensais dire qu'à partir d'un sommet $x$ d'ordre 3 (en tenant compte de mon message précédent) (le cube inscrit est fixé) les six éléments $x+(0,0,i)$, $i$ entre 1 et 6 sont les trois arêtes qui touchent le sommet et, soit (type 1) deux sommets reliés à x et une face qui contient ces deux sommets et x, soit (type 2) deux faces qui contiennent x et le sommet commun (en plus de x) à ces deux faces.
Je crois aussi que la compatibilité avec la symétrie implique que l'opposé d'un élément est la k-face opposée, et que le solide tout entier est le neutre
Le sommets commun aux face violet cyan et jaune sur le dessin est de type 2 en les faces qui sont majoritairement cyan et jaunes, le sommet opposé diagonalement (diagonale de la face carrée du haut) à ce dernier est aussi de type 2, les deux autres sur la face du haut sont de type 1, par symétrie on déduis le type des quatre autres sommets d'ordre 3
Donc je pense qu'on a trouvé l'addition, qu'en pensez vous?
Des idées pour la multiplication? -
chew pour le tétraèdre il faut rajouter deux éléments le solide tout entier et le vide, l'anneau correspondant est l'anneau de Boole à 16 éléments
Je ne sais pas si l'addition est raisonnable, et la multiplication n'est pas celle de l'anneau produit
Et pardon j'aurais du fixer le cube inscrit -
Attends j'ai un peu de mal à te suivre : pourquoi pour le tétraèdre on devrait rajouter le "vide" et pas pour le dodécaèdre?
J'ai du mal à comprendre ta construction avec le tétraèdre, déjà : tu dis que c'est $\mathbb F_2^4$, mais tu dis que la multiplication n'est pas la bonne. Que veux-tu dire lorsque tu dis que l'addition est compatible aux symétries ? Ca veut dire quoi ?
Et pourquoi dis-tu que c'est $\mathbb F_2^4$ ? ca pourrait être n'importe quel anneau de cardinal 16 non? Pourquoi ça serait celui-là en particulier ?
Je comprends pas tes formules pour l'ordre et leurs caractérisation par des égalités : est-ce que c'est un axiome (tu as décidé que ça devait être comme ça), ou bien un truc que tu as démontré (et dans ce cas, il faudrait définir le produit).
Bref, je suis un peu perdu. -
chew écrivait:
> Attends j'ai un peu de mal à te suivre : pourquoi
> pour le tétraèdre on devrait rajouter le "vide"
> et pas pour le dodécaèdre?
Je sais pas peut être parce qu'il est autodual
> J'ai du mal à comprendre ta construction avec le
> tétraèdre, déjà : tu dis que c'est $\mathbb F_2^4$, mais tu dis que la multiplication n'est
> pas la bonne.
Sisi pour le tétraèdre c'est le produit direct la multiplication, je parlais du dodécaèdre
> Que veux-tu dire lorsque tu dis que
> l'addition est compatible aux symétries ? Ca veut
> dire quoi ?
Je voulais dire que si on prend deux éléments sur le solide, qu'on les additionnes, et qu'après on prend la symétrie centrale de cenre le milieu du solide (je pense que ça marche que pour cette symétrie), en prenant les éléments qui sont à la même place que ceux d'avant et qu'on les additionnes on obtiens l'élément à la même place que quand on a fait l'addition sur les éléments sans faire la symétrie
> Et pourquoi dis-tu que c'est $\mathbb F_2^4$ ? ca
> pourrait être n'importe quel anneau de cardinal
> 16 non? Pourquoi ça serait celui-là en
> particulier ?
Parce que à une face du tétraèdre on associe ses sommets, cela correspond sur l'anneau à mettre à 1 ces sommets et à 0 les autres
Aussi peut être parce que l'addition est compatible avec la symétrie centrale et l'ordre s'exprime avec la multiplication
> Je comprends pas tes formules pour l'ordre et
> leurs caractérisation par des égalités : est-ce
> que c'est un axiome (tu as décidé que ça devait
> être comme ça), ou bien un truc que tu as
> démontré (et dans ce cas, il faudrait définir
> le produit).
Pour le produit dans le cas du tétraèdre et du cube c'est le produit de l'anneau produit. Pour le tétraèdre l'ordre veut juste dire que 0 est plus petit que 1 et qu'on prend l'ordre sur $\mathbb{F}_2^4$ composante par composante. De même pour l'octaèdre l'équation de l'ordre c'est pour dire que 0 est plus petit que 1 et 2 et que 1 et 2 sont incomparables et qu'on prend l'ordre composante par composante -
Pour les équation des ordre on peut démontrer que ce sont des ordres pour les cas infini
pour les anneau de Boole:
réflexivité triviale,
$x\leq y$ et $y\leq x$ implique $x=xy$ et $y=xy$ donc $x=y$
Si $x\leq y$ et $y\leq z$ alors $x=xy$ et $y=yz$ donc $x=xyz=xz$
Pour les 3-anneaux :
réfléxivité triviale
$x\leq y$ et $y\leq x$ implique $x=x^2y$ et $y=y^2x$ donc $x=x^2y^2x=xy^2=y$
Si $x\leq y$ et $y\leq z$ alors $x=x^2y$ et $y=y^2z$ donc $x=x^2y^2z=xyz=x^3yz=x^2z$
Merci de ta réponse
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres


