A propos de zeta impair
Bonjour,
En cherchant à écrire zeta(3) à partir de la formule de pi, à partir de Wolfram :
Pi = 4 Sum[(-1)^k/(2 k + 1), {k, 0, Infinity}]
la fonction zeta de Hurwitz
est apparue par hasard et je ne la connais pas.
J'ai pu alors formuler, grâce à wolfram, les relations suivantes
pi^3=zeta[3,1/4] - 28*zeta[3]
pi^5=3/5(zeta(5,1/4) - 496 zeta(5))
pi^7=45/122 (zeta(7,1/4) - 8128 zeta(7))
d'où cette relation pour zeta(2) avec zeta impair.
Y aurait-il quelque chose à apprendre de ces formules, comme l'éventuelle transcendance de zeta impair ?
Merci
En cherchant à écrire zeta(3) à partir de la formule de pi, à partir de Wolfram :
Pi = 4 Sum[(-1)^k/(2 k + 1), {k, 0, Infinity}]
la fonction zeta de Hurwitz
est apparue par hasard et je ne la connais pas.
J'ai pu alors formuler, grâce à wolfram, les relations suivantes
pi^3=zeta[3,1/4] - 28*zeta[3]
pi^5=3/5(zeta(5,1/4) - 496 zeta(5))
pi^7=45/122 (zeta(7,1/4) - 8128 zeta(7))
d'où cette relation pour zeta(2) avec zeta impair.
Y aurait-il quelque chose à apprendre de ces formules, comme l'éventuelle transcendance de zeta impair ?
Merci
Réponses
-
Dans le domaine on connait (au moins) deux résultats spectaculaires:
$\zeta(3)$ est un nombre irrationnel. Découvert par un mathématicien français, Apéry, qui avait plus de 40 ans quand il a donné une preuve (incomplète?) de ce résultat. :-)
L'autre résultat, est aussi du à un français, Rivoal, qui a prouvé, sauf erreur, que parmi la suite des nombres:
$\zeta(2n+1)$ , une infinité était irrationnels. (mais on ne sait pas lesquels précisément). -
Je suis preneur, pour commencer, d'une preuve de:
$\pi^3=\zeta(3,1/4) - 28\zeta(3)$ -
Je suis celui qui a posé la question
Impossible de répondre - data base error ?? -
pseudo abs qui a des difficultés pour répondre
Merci pour tes réponses :
Oui, je suis au courant de ta première réponse, même si je n'ai pas les outils pour comprendre la plupart des démos. Pour le reste on verra...
http://www.larecherche.fr/actualite/mathematiques/multizetas-sortent-ombre-01-05-2012-91126
http://maths.mq.edu.au/~alf/Humid%20Summer/45.pdf
http://www.math.u-psud.fr/~bouillot/OB_The_Algebra_of_Multitangent_Functions.pdf -
Ce que je trouve fascinant, c'est la présence des trois premiers nombres parfaits plus grands que 6...vers une preuve qu'il existe une infinité de nombres parfaits ?
-
Sylvain, c'est la perfection de votre (ta) mémoire qui parfait ce topic impair-fait de coefficient parfaits -:)
C''est moi qui ai bidouillé les formules en les rendant le plus simple possible, et il y a d'autres coefficients possibles avec 3/4,5/4....
S'il s'avère que ces coefficients sont les plus petits, alors on pourrait penser qu'il y a une relation entre les premiers 2,3,5,7...
car pi^2=6zeta(2), sauf que zeta(2/1/4) n'est pas nul. -
Je ne vois pas, sauf erreur, de preuve de l'identité: $\pi^3=\zeta(3,1/4) - 28\zeta(3)$ dans les textes mis en lien ci-dessus.
-
La partie n'est pas gagnée en effet, mais ce n'est pas forcément la fin.
Si la relation était établie, il n'y aurait pas de preuve à faire.
C'est justement la difficulté de l'affaire qui fait ici débat, frère. -
Wolfram, en ligne, indique bien que zeta[3,1/4] - 28*zeta[3] est égal à $\Pi^3$.
Ce n'est pas une preuve en soi mais un signe encourageant. -
pi^9=63 zeta(9,1/4))/277- 8241408 zeta(9)/277
pi^11=14175 zeta(11,1/4)/101042 -14856307200 zeta(11)/50521 -
$\pi^3=\zeta(3,1/4) - 28\zeta(3)$ est équivalente, sauf erreur, à:
$\displaystyle \pi^3=36\sum_{k=0}^{+\infty}\dfrac{1}{(4k+1)^3}-28\sum_{k=0}^{+\infty}\dfrac{1}{(4k+3)^3}-\dfrac{7}{2}\zeta(3)$ -
Abstract:
Si tu joues avec un algorithme de type LLL, attention à la précision des constantes.
Pari GP met trop de temps à calculer des valeurs de la fonction zeta de Hurwitz avec une bonne précision. -
Fin de partie,
ta formule est intéressante.
reprise pour les coefficients du post précedent :
pi^3=zeta[3,1/4] - 28*zeta[3]
pi^5=3/5(zeta(5,1/4) - 496 zeta(5))
pi^7=45/122 (zeta(7,1/4) - 8128 zeta(7))
pi^9=63/277 (zeta(9,1/4) - 130816 zeta(9))
pi^11=14175/101042(zeta(11,1/4) - 2096128 zeta(11)) -
A noter que les constantes devant les $\zeta(2k+1)$ sont divisibles par $2^{2k}$
-
Juste pour garder pi^3 et zeta(3)
sum_(k=1)^infinity 1/(4 k+1)^3 = 1/64 (28 zeta(3)-64+pi^3)
http://urlz.fr/AJ9 -
Il connait aussi:

Cela aide pour établir la première identité. -
Il connait également:

et:
Cela aide bien pour établir la deuxième identité. -
De même:

et:
aide bien à établir la troisième identité. -
Cela revient peut-être à se poser une question.
On sait que
pi = 4 sum_(k=0)^infinity (-1)^k/(2 k+1)
pi^2 = 6zeta(2) = 6*Sum[1/k^2, {k, 1, Infinity}]
Mais, peut-on calculer pi^3 selon une somme sans faire appel à zeta(3) ?
http://urlz.fr/AJp -
'bonjour
la première identité donné par abstract (celle en $Z_3$) est exact (on peut le vérifier numériquement) ;
les deux autres (celles en $Z_5$ et $Z_7$) sont erronées (on peut le vérifier numériquement) ,
les coefficients en $Z_5$ et en $Z_7$ sont faux alors que les coefficients en $\pi^5$ et en $\pi^7$ sont exacts
il existe une relation signalée plus haut entre Zeta de Hurwitz telles que $q = \frac{1}{4}$
et les séries de Riemann $$\Sigma_1^{+\infty}\frac{1}{(4n-3)^x}$$
et on part de la relation (démontrée avec chaque série exprimée et développée) :
$$Z_i(x) + Z_{ai}(x) = 2\Sigma_1^{+\infty}\frac{1}{(4n-3)^x}$$
avec la série des impairs $Z_i(x) = \Sigma_0^{+\infty}\frac{1}{(2n+1)^x} = (1 - 2^{-x})Z_x$
et aussi la série alternée des impairs : $Z_{ai}(x) = \Sigma_0^{\infty}\frac{(-1)^n}{(2n+1)^x}$
en particulier on connaît (calculées avec les nombres d'Euler)
$Z_{ai}(3) = \frac{\pi^3}{32}$ ; $Z_{ai}(5) = \frac{5\pi^5}{1536}$ et enfin : $Z_{ai}(7) = \frac{61\pi^7}{184320}$
pour $x = 3$ il vient : $\frac{7}{16}Z_3 + \frac{\pi^3}{64} = \Sigma_1^{+\infty}\frac{1}{(4n-3)^3}$
pour $x = 5$ il vient : $\frac{31}{64}Z_5 + \frac{5\pi^5}{3072} = \Sigma_1^{+\infty}\frac{1}{(4n-3)^5}$
pour $x = 7$ il vient : $\frac{127}{256}Z_7 + \frac{61\pi^7}{368640} = \Sigma_1^{+\infty}\frac{1}{(4n-3)^7}$
cordialement -
Tu veux dire que wolfram se trompe ?
http://urlz.fr/AJN
Celle de zeta(3) par "fin de partie" est fausse
http://urlz.fr/AJS
A quel calculateur se fier ? -
-
Tu as mal recopié la formule que je proposais il s'agit de:

(ton deuxième terme n'est pas le bon)
Wolfram donne ce calcul:
Si on développe le premier membre on a bien qu'il est égal à:
$\pi^3$ -
Tout à fait, excuse moi
-
La deuxième formule est correcte (numériquement), probablement une erreur de lecture.
$\pi^5=\dfrac{3}{5}\Big(\zeta(5,1/4) - 496 \zeta(5)\Big)$ -
Voir aussi, à la suite des explications de Jean:
http://fr.wikipedia.org/wiki/Fonction_bêta_de_Dirichlet -
Noté, bonsoir - A+
-
@Sylvain et les nombres parfaits :
La séquence 2^(4n+1)-2^(2n) voir http://oeis.org/A079598
donne certains nombres parfaits ( http://oeis.org/A000396 ) qui se trouvent dans les relations de ce topic.
pi^3=zeta[3,1/4] - 28*zeta[3]
pi^5=3/5(zeta(5,1/4) - 496 zeta(5))
pi^7=45/122 (zeta(7,1/4) - 8128 zeta(7))
pi^9=63/277 (zeta(9,1/4) - 130816 zeta(9))
pi^11=14175/101042(zeta(11,1/4) - 2096128 zeta(11))
@...
Pour pi^3, par exemple,on peut faire ces autres choix
pi^3=28 zeta(3)-64 sum_(k=0)^infinity 1/(4 k+3)^3
pi^3=-28 zeta(3)+64 sum_(k=0)^infinity 1/(4 k+1)^3
pi^3 = 28 zeta(3)-64 sum_(k=1)^infinity 1/(4 k-1)^3
pi^3 = -28 zeta(3)+64 sum_(k=1)^infinity 1/(4 k-3)^3
ce qui donne avec l'un d'entre eux
pi^3 = 4 (7 zeta(3)-16 sum_(k=0)^infinity 1/(4 k+3)^3)
pi^5 = 48/5 (31 zeta(5)-64 sum_(k=0)^infinity 1/(4 k+3)^5)
pi^7 = 1440/61 (127 zeta(7)-256 sum_(k=0)^infinity 1/(4 k+3)^7)
pi^9 = 80640/1385 (511 zeta(9)-1024 sum_(k=0)^infinity 1/(4 k+3)^9)
La sequence 16,64,256,1024...voir http://oeis.org/A000302
est celle de 4^n
La séquence 7,31,127,511 ...http://oeis.org/A083420
est celle de 2*4^n-1
ce qui est sympa car c'est celle de la somme des diviseurs de 4^n
:-) -
C'est bien joli tous ces calculs mais où sont les preuves? B-)-
Pour commencer je suis intéressé par la preuve de celle-ci:
$\displaystyle \pi^3=36\sum_{k=0}^{+\infty}\dfrac{1}{(4k+1)^3}-28\sum_{k=0}^{+\infty}\dfrac{1}{(4k+3)^3}-\dfrac{7}{2}\zeta(3)$
J'ai bien une idée mais les calculs m'ont l'air fastidieux et j'ignore s'ils aboutissent réellement à quelque chose.
$\pi^3=6\times \dfrac{\pi^2}{6}\times 4\times \dfrac{\pi}{4}$ et $\dfrac{\pi^2}{6},\dfrac{\pi}{4}$ sont exprimables chacune sous forme de séries. Je ne sais pas si cela aboutit vraiment quelque part. -
pi^3...Wolfram
Perso, pour le calcul, j'abdique
http://gilles.costantini.pagesperso-orange.fr/prepas_fichiers/zeta2.pdf -
C'est aussi intéressant de savoir d'où ces formules viennent que les formules elles-mêmes.
Peut-être n'es-tu pas familiarisé avec ceci:
Il existe un algorithme presque magique qui permet de détecter des dépendances intégrales entre plusieurs nombres calculés avec une bonne précision.
Une dépendance intégrale signifie qu'il te trouve une relation entre $n$ nombres $x_1,...,x_n$
: $a _1\times x_1+a_2\times x_2+...+a_n\times x_n=0$ , les $a_i$ sont des entiers.
Pour voir si la relation n'est pas bidon ou de circonstance, tu augmentes la précision avec laquelle sont calculés les $n$ nombres $x_1,....x_n$ et si les coefficients obtenus restent identiques alors il y a de fortes chances que la relation obtenue ne soit pas bidon.
En général, si au premier essai tu trouves des coefficients qui sont relativement petits et si ton nombre de $x_i$ est faible alors c'est un signe que tu as trouvé une relation qui n'est pas liée à la précision choisie pour le calcul des $x_i$.
Cet algorithme ne prouve rien, il permet juste de formuler des conjectures sur la dépendance de nombres.
J'imagine que des tonnes de formules conjecturées de la sorte, attendent toujours d'être prouvées. B-) -
Abstract:
Tes liens sont intéressants mais il faut savoir que le calcul de $\zeta(2)$ est assez bien documenté.
C'est un sujet récurrent sur ce forum.
Mais le calcul de la fonction $\displaystyle \beta(s)=\sum_{k=0}^{+\infty} \dfrac{(-1)^{n}}{(2n+1)^s}$ pour $s$ entier impair
est bien moins documenté. Je n'ai pas (encore) trouvé de documents élémentaires sur la sujet.
L'article de Wikipedia qui lui est consacré énonce bien une formule, mais il ne pousse pas le détail à fournir une preuve voire même une référence précise dans la littérature mathématique où trouver une telle preuve. -
Pour info concernant la cotangente, car je ne sais pas programmer :
« Il existe de nombreux algorithmes de calcul de PI, chacun adapté au type de machine ou de performance que l'on veut obtenir. Ici nous avons utilisé un algorithme simple: la formule de Machin:
PI = 16arctg(1/5) - 4arctg(1/239)
Cette formule n'est pas la meilleure mais la plus simple à mettre en oeuvre, et elle s'avère performante sur des machines à mots de 32 bits pour calculer quelques miliers de décimales. La difficulté de l'implémentation réside dans la mise en oeuvre des calculs en muliprécision nécessaires pour le calcul de plusieurs centaines de milliers de décimales. Comment faire ? Cliquez. »
http://www.brouty.fr/Maths/pi.html
Autres approches
http://maths.amatheurs.fr/index.php?page=pi
Trigo, Bernoulli, Buffon (probabilité) ...
http://www.pi314.net/fr/buffon.php
on peut même mélanger ce que tu sais :
http://www.les-mathematiques.net/phorum/read.php?2,723648
Pour Buffon, une visite à Montbard s’impose si on va près d’Auxerre, car ce n'était pas un rêveur. Les forges sont une usine intégrée ; "les lieux sont en effet pensés pour l'optimisation des étapes de la fabrication. Ils rassemblent les installations industrielles, la maison du maître et les habitations ouvrières en un même espace" Wiki
Peut-être les prémices de ces autres entreprises à la fois « intégrées » et au concept idéaliste du 19e siècle, comme la chocolaterie Menier (désormais administration Nestlé, à visiter impérativement (être patient le jour du Patrimoine) tant les constructions sont magnifiques, banlieue est de Paris) ou le familistère Godin actuellement rénové (poêle à bois des écoles communales, entre autres ; situé dans le Thiérache) où l’ouvrier avait une noble place ; un théâtre avait été construit juste pour eux au familistère ! On peut le visiter. -
La méthode de recherche empirique de relations intégrales entre nombres, mentionnée plus haut, a été utilisés pour trouver la formule:
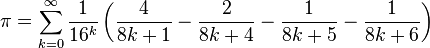
Voir: http://fr.wikipedia.org/wiki/Formule_BBP -
Oui, à ce soir si tvb
[Que veut dire cet acronyme "tvb" ? Ne peux-tu écrire de façon à ce qu'on te comprenne ? AD] -
Trouver une relation entre $\displaystyle \sum_{n=0}^{+\infty}\dfrac{1}{(4n+1)^s}$ et $\displaystyle \sum_{n=0}^{+\infty}\dfrac{1}{(4n+3)^s}$, $\zeta(s)$
est un calcul "algébrique":
$\zeta(s)=\displaystyle \sum_{n=1}^{+\infty}\dfrac{1}{n^s}=\sum_{n=1}^{+\infty}\dfrac{1}{(2n)^s}+\sum_{n=0}^{+\infty}\dfrac{1}{(2n+1)^s}=\dfrac{1}{2^s}\sum_{n=1}^{+\infty}\dfrac{1}{n^s}+\sum_{n=0}^{+\infty}\dfrac{1}{(2n+1)^s}=\dfrac{1}{2^s}\zeta(s)+\sum_{n=0}^{+\infty}\dfrac{1}{(2n+1)^s}$
Ainsi:
$\displaystyle \sum_{n=0}^{+\infty}\dfrac{1}{(2n+1)^s}=\Big(1-\dfrac{1}{2^s}\Big)\zeta(s)$
$\displaystyle \zeta(s)= \sum_{n=1}^{+\infty}\dfrac{1}{(4n)^s}+ \sum_{n=0}^{+\infty}\dfrac{1}{(4n+1)^s}+\sum_{n=0}^{+\infty}\dfrac{1}{(4n+2)^s}+\sum_{n=0}^{+\infty}\dfrac{1}{(4n+3)^s}$
$\displaystyle \zeta(s)=\dfrac{1}{4^s}\sum_{n=1}^{+\infty}\dfrac{1}{n^s}+ \sum_{n=0}^{+\infty}\dfrac{1}{(4n+1)^s}+\dfrac{1}{2^s} \sum_{n=0}^{+\infty}\dfrac{1}{(2n+1)^s}+\sum_{n=0}^{+\infty}\dfrac{1}{(4n+3)^s}$
$\displaystyle \zeta(s)=\dfrac{1}{4^s}\zeta(s)+ \sum_{n=0}^{+\infty}\dfrac{1}{(4n+1)^s}+\dfrac{1}{2^s}\Big(1-\dfrac{1}{2^s}\Big)\zeta(s)+\sum_{n=0}^{+\infty}\dfrac{1}{(4n+3)^s}$
$\displaystyle \zeta(s)=\dfrac{1}{2^s}\zeta(s)+\sum_{n=0}^{+\infty}\dfrac{1}{(4n+1)^s}+\sum_{n=0}^{+\infty}\dfrac{1}{(4n+3)^s}$
Ainsi:
$\displaystyle\sum_{n=0}^{+\infty}\dfrac{1}{(4n+3)^s}=\Big(1-\dfrac{1}{2^s}\Big)\zeta(s)-\sum_{n=0}^{+\infty}\dfrac{1}{(4n+1)^s}$ -
tvb tout va bien
[Économiser 7 lettres et produire un message que personne ne comprend ! Où est l'intérêt ?
Sans compter la charte 3.3.4. AD] -
Tu veux trouver une dépendance intégrale entre $\zeta(3)$ et $\zeta(2)$, c'est à dire que tu crois qu'on peut écrire:
$\zeta(3)=\dfrac{p}{q}\zeta(2)$ avec $p,q$ des entiers non nuls ?
Désolé, on ne peut pas. :-D -
Avec une somme
-
Si on pose $c=b-a$ on a:
$b=c+a$ B-) -
c=zeta(3)
a=zeta(2)
Que proposes-tu pour b ? -
$\zeta(3)=\Big(\zeta(3)-\zeta(2)\Big)+\zeta(2)$
Il faut être plus précis dans ta demande.
On ne sait pas grand chose sur $\zeta(3)$ hormis qu'il est irrationnel. -
On est d'accord ... je n'y arrivais pas non plus.
Avec OEIS, j'arrive à exprimer pi^n pour n impair, selon les relations données plus haut, exemple :
soit avec m=n-1 et le nombre d'Euler_m
(E_m)*pi^n = 2 (n-1)! ((2^n-1) zeta(n) - 2^(n+1) sum_(k=0)^infinity 1/(4 k+3)^n)
Nombres d'Euler http://fr.wikipedia.org/wiki/Nombre_d'Euler
pour n=7, avec E_6=61
pi^7 = 1440/61 (127 zeta(7)-256 sum_(k=0)^infinity 1/(4 k+3)^7)
61*pi^n = 2 (7-1)! ((2^7-1) zeta(7)-2^(7+1) sum_(k=0)^infinity 1/(4 k+3)^7)
calcul wolfram -
Fin de partie écrivait:
> Je ne vois pas, sauf erreur, de preuve de
> l'identité: $\pi^3=\zeta(3,1/4) - 28\zeta(3)$
> dans les textes mis en lien ci-dessus.
Le problème est donc de calculer $$\sum_{n=1}^{\infty} \frac{1}{(4n-3)^3}.$$ Sauf erreur,
$$\sum_{n=1}^{\infty} \frac{1}{(4n-3)^3}=\lim_{N\to\infty}\frac{1}{128}\bigl(\psi^{(2)}(1/4 + N)-\psi^{(2)}(1/4)\bigr)=-\frac{1}{128}\psi^{(2)}(1/4).$$ Ensuite rdv ici (29) :
http://mathworld.wolfram.com/PolygammaFunction.html -
NicoKH:
Merci pour l'indication mais je ne vois pas en quoi cela constitue une preuve élémentaire. A moins que l'énoncé (29) soit une évidence B-)-. Ce que je ne pense pas.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.8K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




