Métrique à symétrie sphérique
dans Analyse
Bonsoir,
Je désirerais mieux comprendre la démonstration du théorème de Birkhoff (les solutions de l'équations d'Einstein dans le vide à symétrie sphérique sont les métriques de Schwarzschild). Mais presque toutes les démonstrations que j'ai trouvées commencent en supposant que la métrique a déjà une forme sympathique. D'autres expliquent comment y arriver mais admettent un résultat que je ne sais pas démontrer.
page 65: http://d.umn.edu/~vvanchur/2013PHYS5551/Chapter5.pdf
Si je comprends bien, il s'agit de montrer que si une variété pseudo-Riemannienne de dimension $n$ admet un feuilletage composé de sous-variétés de dimension $m$ (et "maximally symmetric") alors la métrique est de la forme (il existe une carte tel que la métrique soit de la forme) $$ ds^2=g_{IJ}(v)dv_Idv_J +f(v)h_{ij}(u)du_idu_j $$ où $(u_i)$ avec $i \in \{1,\ldots,m\}$ et $(v_I)$ avec $I \in \{1,\ldots,n-m\}$
Quelqu'un connaîtrait-il une référence ? (celles que j'ai trouvé font ça de manière heuristique et sont très peu détaillées).
Merci.
Je désirerais mieux comprendre la démonstration du théorème de Birkhoff (les solutions de l'équations d'Einstein dans le vide à symétrie sphérique sont les métriques de Schwarzschild). Mais presque toutes les démonstrations que j'ai trouvées commencent en supposant que la métrique a déjà une forme sympathique. D'autres expliquent comment y arriver mais admettent un résultat que je ne sais pas démontrer.
page 65: http://d.umn.edu/~vvanchur/2013PHYS5551/Chapter5.pdf
Si je comprends bien, il s'agit de montrer que si une variété pseudo-Riemannienne de dimension $n$ admet un feuilletage composé de sous-variétés de dimension $m$ (et "maximally symmetric") alors la métrique est de la forme (il existe une carte tel que la métrique soit de la forme) $$ ds^2=g_{IJ}(v)dv_Idv_J +f(v)h_{ij}(u)du_idu_j $$ où $(u_i)$ avec $i \in \{1,\ldots,m\}$ et $(v_I)$ avec $I \in \{1,\ldots,n-m\}$
Quelqu'un connaîtrait-il une référence ? (celles que j'ai trouvé font ça de manière heuristique et sont très peu détaillées).
Merci.
Réponses
-
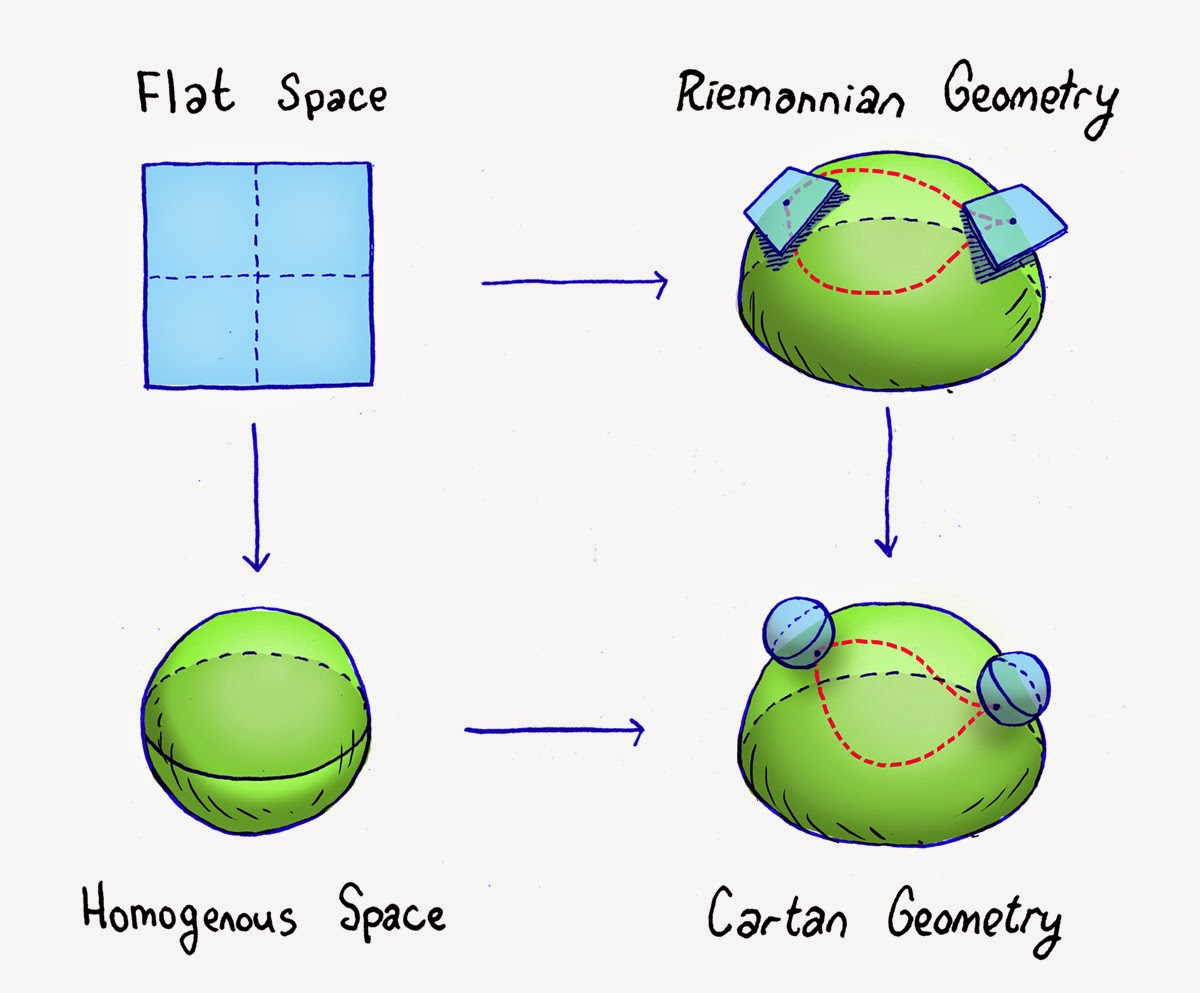
Un panorama visuel des différentes géométries à traiter dont celle Riemannienne s'impose à la compréhension en s'exposant:
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres
In this Discussion
Qui est en ligne 2
2 Invités