Fonction génératrice des nombres de Bernoulli

L2M · April 2016

Grand salut à tous les matheux.

Voici la situation,
La fonction génératrice exponentielle des nombres de Bernoulli est $\dfrac z {e^z-1}$ :

$\dfrac z{e^z-1}=\sum_{n=0}^{\infty}B_n\frac {z^n}{n!}$ (Bn sont les nombres de Bernoulli)

Je suis à la recherche de la fonction génératrice exponentielle des carrés des nombres de Bernoulli. soit f cette fonction :

$f(z)=\sum B_n^2\frac {z^n}{n!} $

Merci pour votre aide.

L2M · April 2016

Si vous avez besoin de plus de détails je suis à votre disposition

P. · April 2016

On pourrait calculer $\sum B^2_n z^n/(n!)^2$ par la methode suivante si $f=\sum u_nz^n $ et $g=\sum v_nz^n$ alors $ h=\sum u_nv_nr^{2n}$ s'obtient par $\frac{1}{2\pi}\int _{0}^{2\pi}f(re^{it})g(re^{-it})dt.$. Mais cela n'est pas exactement ton probleme.

L2M · April 2016

Merci

Cela peut effectivement m'aider.

Pouvez-vous m'envoyer un extrait de cours lié à ce théorème ou le nom du chapitre.

YvesM · April 2016

Bonjour,

C'est pas pour te casser le moral, mais ce serait une prouesse inouïe que de trouver cette fonction $\displaystyle f(z) = \sum_{k\geq 0} B_k^2 {z^k \over k!}$ sous une forme utile... si tu trouves un truc, poste-le s'il te plaît.

L2M · April 2016

salut

Je le ferai avec plaisir.

Merci pour votre soutien.

L2M · April 2016

En fait, je cherche à calculer la valeur exacte de la constante d'Euler (gamma). ça fait un mois que j'ai pu établir une relation entre gamma et la fonction citée en haut.

Trouver cette fonction c'est trouver la valeur exacte de gamma.

Rescassol · April 2016

Bonne nuit,

HoHo !! Ça sent le transfert en shtam.

Cordialement,

Rescassol

YvesM · April 2016

Bonjour,

C'est pour cela que je parle de prouesse inouïe... intuitivement, la forme $B_k^2 z^k / k!$ n'a aucune chance d'avoir une forme utile au calcul...

Ceci dit, si tu as établi une relation vraie avec la constante d'Euler, c'est déjà un résultat qui vaut le détour.

Si tu le partages en une proposition mathématique, on peut vérifier.

L2M · April 2016

salut,
c'est quoi le "shtam", je ne suis pas de "blad"

YvesM · April 2016

Bonjour,

Shtam c'est le forum réservé aux démonstrations qui n'en sont pas écrites par des amateurs peu éclairés.

Rien ne dit que ta trouvaille appartient à ce forum. On ne le saura que si tu partages ta trouvaille sous forme d'une proposition mathématique.

gb · April 2016

L2M a écrit:

Trouver cette fonction c'est trouver la valeur exacte de gamma.

La valeur exacte de $\gamma$ est connue : $\gamma = -\Gamma'(1)$.

L2M · April 2016

Il y a de nombreuses formules intégrale pour écrire La constante d'Apéry (la valeur en 3 de la fonction de Riemann) et pourtant on n'a jamais dit qu'on a trouvé sa valeur exacte.

la fonction Gamma est définit par une intégrale. ce n'est pas une fonction exactement définie.

Dire exacte c'est comme zêta(2)=PI^2/6.

YvesM · April 2016

Bonjour,

@L2M, partage ce que tu as trouvé... le reste ne compte pas.

L2M · April 2016

Je n'ai pas l'habitude de partager que ce que j'ai bien vérifié et testé.

L'important c'est d'affirmer la possibilité de trouver cette fonction ou non, ce qui est le sujet actuel.

Merci.

gb · April 2016

Quelle est la valeur exacte de $pi$ (qui intervient dans l'expression de $\zeta(2)$) ?

YvesM · April 2016

Bonjour,

Tu es libre.

Cependant, n'oublie pas que tu peux avoir vérifié et bien vérifié mille fois une proposition de démonstration, ceci ne la rend pas correcte pour autant, n'est-ce pas ?

On peut tout trouver en mathématique, absolûment tout, y compris ce qui est faux.

Je ne sais plus quel est le sujet que tu cherches à discuter. On te souhaite bonne chance pour trouver une forme utile à la série que tu as écrite. C'est tout, il n'y a pas de débat sur ce point.

L2M · April 2016

pi n'est pas exacte mais la trouvaille d'Euler pi^2/6 est élégante.

L2M · April 2016

Merci P. pour ton aide précieuse

zorn1 · April 2016

Pi n'est-il pas le double de la valeur du plus petit zéro strictement positif de la fonction cosinus ( définie comme la somme d'une série entière)?

P. · April 2016

@L2M: la demonstration de ce que j'ai ecrit tient en une ligne $\frac{1}{2\pi}\int_0^{2\pi}e^{2i\pi(n-m)t}dt=1$ si $m=n$ et $0$ sinon.

Siegfried · April 2016

Bonjour,

C'est une définition de pi, oui, Zorn1. Je pense que gb essaye de faire passer l'idée que la notion de valeur exacte est ambigüe, L2M aurait dû essayer de le faire (ce qu'il entend par) pour rendre la discussion intelligble.

L2M · April 2016

Merci P.

L2M · April 2016

Je vais vous parler de ma motivation pour ce sujet.

Imaginer qu'on arrive à déterminer des fonctions $f_1$, $f_3$, $f_5$, ... telles que chaque fonction détermine respectivement la valeur de $\gamma=Zêta(1)$, $\Zêta(3)$, $\Zêta(5)$, ...

Exemple $\displaystyle f_1(z) = \sum_{k\geq 0} B_k^2 {z^k\over k!}$ et [large]$\gamma$[/large] s'écrit en fonction de $f_1({\pi\over 2})$

C'est mon rêve pour l'instant.

gebrane · April 2016

Bonjour
Si je pose $$f_1(x)= 1 - \int_x^{+\infty} \frac{\{t\}}{t^2} \, \textrm{d}t$$ avec $\{t\}$ la partie fractionnaire de t. On a $f_1(1)=\gamma$

L2M · April 2016

il y a aussi

$1152d0d7baae35b13f508135bdac94d0.png$
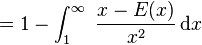
$2ca0c568896a3dbfa16b6a23cec9ed0a.png$
$3dc4b5b6d2c44bcaf4a5c3e558d06dd1.png$
$72246f6a17e79b300afa0ac728cb0f4f.png$
$6dfe41b86a829a512470d67639fc1d6c.png$
https://upload.wikimedia.org/math/3/8/c/38ca20d1a17560eb631cb9b7696682e8.png

je crois que mon $f_1$ est différente c'est tout

L2M · April 2016

Ma question est: y a t il une chance de formuler la série $\sum_{n=0}^{\infty}B_n^2\frac{z^n}{n!}$ comme

$\sum_{n=0}^{\infty}B_n\frac{z^n}{n!}=\dfrac z{e^z-1}$

L2M · April 2016

P. · April 2016

Formellement si la fonction que tu cherches est $F$ tu peux toujours ecrire que le $h$ du premier message est la transformee de Borel de $F$, c'est a dire $\int_0^{\infty}e^{-zx}F(x)dx=h(1/z).$ C'est bien formel, car on ne manipule pas des fonctions entieres. Il faudrait consulter d'autres personnes du forum comme joapa, car je n'y connais rien.

rémi · April 2016

Vu toutes les relations avec des $B_{2n}$, as-tu essayé de chercher des liens entre les $B_{2n}$ et les $B^{2}_{n}$ ?

L2M · April 2016

- P. Affirmatif, F n'est pas entière

- rémi : Tous les $B_{2n+1}$ sont nuls sauf $B_{1}$

L2M · April 2016

les $B_{n}$ sont manipulables par la relation de récurrence
https://upload.wikimedia.org/math/2/1/f/21f7d756967bbf2c62d29fc937fe50aa.png
et
https://upload.wikimedia.org/math/1/b/c/1bcbe62482e259e8317e1f19aa0983c0.png

C'est difficile de trouver une telle relation pour les $B_{n}^2$

gebrane · April 2016

Mais il y a des formules qui donnent explicitement les $B_n$,non?

L2M · April 2016

La formule dont tu parle est plus compliquée que la relation de récurrence :

https://upload.wikimedia.org/math/5/7/1/5719a41a8db4f20a0acac754d0590bf3.png

https://upload.wikimedia.org/math/1/6/4/164ff803307445448287c2ccd536f58c.png

imagine le carré $B_n^2$

rémi · April 2016

oui, par exemple $$B_n=\underset{k=0}{\overset{n}{\sum}}\frac{1}{k+1}\underset{j=0}{\overset{k}{\sum}}(-1)^j\binom{k}{j}j^n$$

L2M · April 2016

Voila ce que je vais faire, je doit absolument traiter la suggestion de P. du plus près et vous informer du résultat.

Les mathématique c'est comme la vie, c'est une suite d'événements qui changent et se développent au cours du temps. La façon avec laquelle je vois ma question maintenant n'est pas la même d'ici un jour, un mois ou une année ...

P. · April 2016

Attention, puisqu'on baigne dans le formel (bof) il faut prendre conscience que le rayon de convergence $R$ de $\sum B^2_nz^n/n!$ est zero. En effet le rayon de convergence de $\sum B_nz^n/n!$ est $2\pi$ (car $\pm 2i\pi$ sont les plus proches points singuliers pour $z/(e^z-1)$) et on applique le critere $1/R=\limsup (B^2_n/n!)^{1/n}.$

L2M · April 2016

correct,

L2M · April 2016

voir le fichier joint stp P.

P. · April 2016

Non, ton $\delta$ est de rayon de convergence nul aussi. C'est a dire que tu dois t'appuyer sur une theorie parfaitement honorable, les series formelles, qui ont leurs techniques propres comme les equations fonctionnelles, et qui se manient avec plus de precautions que les series entieres.

L2M · April 2016

je vais tout revérifier Merci

je serai de retour bientôt pour un deuxième épisode.

L2M · April 2016

j'ai confiance en ma méthode, le problème c'est que mon ambition est plus grande que mes compétences. c'est pourquoi j'ai choisi ce forum.

Merci pour tout ceux qui ont tenté de m'aider.

L2M · April 2016

Je suis de retour.
Réponse à une contradiction.

Premièrement, est ce que vous êtes tous d'accord que 0 est le rayon de convergence de la série $$\sum_{k=1}^{} B_{2k}|B_{2k}| \frac{(2^{2k}-1)(2^{2k-1}-1)}{2k (2k)!} x^{2k-1}$$

L2M · April 2016

Je vais montrer maintenant que $$
\sum_{k=1}^{\infty} B_{2k}|B_{2k}| \frac{(2^{2k}-1)(2^{2k-1}-1)}{2k (2k)!} \Big(\frac{\pi}{4}\Big)^{2k-1}=\frac{1}{2}\tan\Big(\frac{\pi}{8}\Big)+\frac{4}{\pi}\ln\Big(\cos\big(\frac{\pi}{4}\big)\Big)+\frac{1}{4}$$

L2M · April 2016

d'après la formule d'intégration d'Euler-Maclaurin ...

voir la suite dans le fichier joint ...

gebrane · April 2016

Bonjour,
Un point qui m’échappe, Un rayon de convergence nul signifie qu'il y a divergence en tout point $z\in \C^*$
Je me demande pourquoi, on insiste à calculer une somme qui n'existe pas!

L2M · April 2016

c'est ça la contradiction, je veux voir l'erreur dans le calcul de la somme.

L2M · April 2016

j'aimerais que qqun vérifie les étapes. car ma recherche se base sur cette formule d'Euler-Maclaurin.

gebrane · April 2016

Je ne vois pas de contradiction pour le moment, j'ai bien compris que le rayon de convergence de $\sum B_n^2\frac {z^n}{n!}$ est nul en lisant ce document formule 57 ( meme si la defintion de $B_n$ est un peu differente) mais je ne peux rien conclure sur le rayon de convergence de $\sum_{k=1}^{} B_{2k}|B_{2k}| \frac{(2^{2k}-1)(2^{2k-1}-1)}{2k (2k)!} x^{2k-1}$ pour le moment

L2M · April 2016

si on note le $B_n$ de la formule 57 par $b_n$ alors $b_n=(-1)^nB_{2n}$

donc la formule 57 par les $B_n$ qu'on traite devient

$B_{2n} \sim (-1)^n\frac{2(2n)!}{(2\pi)^{2n}}$

les $b_n$ sont tous positifs

L2M · April 2016

.......

Fonction génératrice des nombres de Bernoulli

Réponses

Bonjour!

Catégories

In this Discussion

Qui est en ligne 40