Séquences récurrentes de premiers potentiels
dans Analyse
Bonjour à tous,
j'ai fait un calcul sur des séquences récurrentes de nombres premiers potentiels apparaissant dans le crible d'Ératosthène et je trouve cette correspondance :
Est-ce que quelqu'un aurait une idée pour m'aider ?
Merci
PS. Désolé si ce n'est pas dans la bonne section, je n'ai aucune idée de ce dont il s'agit :-)
j'ai fait un calcul sur des séquences récurrentes de nombres premiers potentiels apparaissant dans le crible d'Ératosthène et je trouve cette correspondance :
2 0,5 3 0,3333333 5 0,2666667 7 0,2285714 11 0,2077922 13 0,1918082 17 0,1805254 19 0,171024 23 0,1635882J'essaye de trouver la fonction qui s'en approche du plus près possible (voire exactement, ce qui serait fantastique) mais je n'ai pas tellement de "méthode" pour faire ça du coup c'est un peu n'importe quoi mes fonctions, genre f(p)=0.2/ln(p) ... 8-)
Est-ce que quelqu'un aurait une idée pour m'aider ?
Merci
PS. Désolé si ce n'est pas dans la bonne section, je n'ai aucune idée de ce dont il s'agit :-)
Réponses
-
Cela m'a l'air relié à la proportion de nombre premiers qui sont plus petits qu'un entier fixé!
C'est très connu, et cela s'appelle le théorème des nombres premiers (il en existe même des versions avec des restes...) -
ha ok... Et c'est quoi la fonction f(p) alors ?
-
$ \prod_{n=1}^{m} [(p_n -1)/p_n] $
exemple pour prime(5)=11
(2-1)(3-1)(5-1)(7-1)(11-1)/(2*3*5*7*11) = 16/77 = 0.207792 ... http://tinyurl.com/ydbvvvw6 -
Ah oui, dans ce cas, tu peux aller voir la formule de Mertens...
-
Super Robusta merci !
-
Est-ce qu'il y a moyen de savoir vers quoi elle tend cette fonction $ f(p) = \prod_{n=1}^{m} [(p_n -1)/p_n] $ en + l'infini ?
-
D'accord, ce serait donc le troisième théorème de Mertens et sa limite en $ + \infty $ :
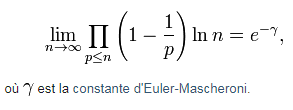
je suppose que c'est "équivalent" à la fonction $ f(p) = \prod_{n=1}^{m} [(p_n -1)/p_n] $ (ça "ressemble" 8-) ) mais j'ai un peu de mal à comprendre pourquoi, c'est quand même un peu différent... Vous pouvez m'expliquer s'il vous plait ?
Et vers quelle valeur tend la fonction de Robusta $ f(p) $ en $ + \infty $ donc ? (c'est déjà une nouvelle incroyable que ça tende vers quelque chose, j'aurais parié que c'était une espèce "d'indéfini" comme on sait si bien en faire en math :-) ...) -
$$\prod_{n=1}^m \left(\frac{p_n - 1}{p_n}\right) = \prod_{n=1}^m \left(1 - \frac{1}{p_n}\right) = \prod_{p \leq p_m} \left(1 - \frac{1}{p}\right) \underset{m \to +\infty}{\sim} \frac{\mathrm{e}^{\gamma}}{\log p_m} \underset{m \to +\infty}{\sim} \frac{\mathrm{e}^{\gamma}}{\log m}$$
-
Mais $ \frac{\mathrm{e}^{\gamma}}{\log m} {\to 0} $ quand $ {m \to +\infty} $
Donc ça veut dire que la proportion maximale de nombre premier $ { \to 0 } $ en $ { +\infty} $
C'est pas en contradiction avec le fait qu'il y a une infinité de nombre premier non ? -
-
Exact. Pour le dernier équivalent que j'ai donné, j'ai utilisé le théorème des nombres premiers sous la forme $$p_m = m \log m(1+o(1))$$ puis le fait que $$\log(m \log m(1+o(1))) = \log(m \log m)(1+o(1)) \underset{m \to +\infty}{\sim} \log m.$$
-
Oui et j'ai regardé un peu les différentes démonstrations, Mertens donc mais aussi Legendre, Gauss et aussi celle d'Erdös et Selberg qui est soit disant élémentaire, mais c'est quand même assez balaise dis donc :-S ... Moi j'ai trouvé ce résultat graphiquement en remarquant les groupes de motifs qui se répètent du crible d'Ératosthène :
Après avoir appliqué le premier nombre premier $p_1$=2 :
on trouve à partir du nombre $p_1$+1=3 des groupes de 2 nombres identiques parmi lesquels 1 nombre sur 2 est potentiellement premier (PP).
Puis après avoir appliqué le deuxième nombre premier $p_2$=3 :
https://i94.servimg.com/u/f94/19/78/67/42/ce-2-310.png
on trouve à partir du nombre $p_2$+1=3 des groupes de 6 nombres identiques parmi lesquels 2 nombres sur 6 sont potentiellement premiers.
Puis après avoir appliqué le troisième nombre premier $p_3$=5 :
on trouve à partir du nombre $p_3$+1=6 des groupes de 30 nombres identiques parmi lesquels 8 nombres sur les 30 sont potentiellement premiers (PP).
Et ainsi de suite avec le quatrième nombre premier $p_4$=7 ou on trouve à partir de $p_4$+1=8 des groupes de 210 dont 48 sont PP et plus généralement grâce à la formule de Robusta pour le n ieme nombre premier $p_n$ on a des groupes "identiques" à partir de $p_n$+1 de $ \prod_{n=1}^{m} p_n $ nombres sur lesquels $ \prod_{n=1}^{m} p_n -1 $ sont PP.
Ce qui correspond en fait à la proportion maximum de nombre premiers dans chaque groupe, et surtout, ça correspond au ratio presque exact de nombre premier au début du groupe, après $p_n$+1 il me semble...
Bon c'est peut-être pas super rigoureux, mais c'est simple pour le coup... Et du coup c'est amusant :-) -
Aussi je me demande si on ne pourrait pas utiliser cette structure de groupe pour les premiers jumeaux :
dans le groupe de $p_2$ de 6 nombres il y à 2 "premiers potentiels" aux positions 2 et 4 qui sont donc répétés à l'infini.
Certains sont d'ailleurs "avérés" premiers dans le groupe de $p_3$ de 30 nombres, et il reste dans ce nouveau groupe 3 "jumeaux premiers potentiels" et ce dans tous les groupes suivant à l'infini également.
N'y a-t-il pas un moyen de prouver qu'un ou plusieurs de ces "jumeaux premiers potentiels" passent forcément au travers du crible des nombres premiers suivant et s'avèrent en premier jumeaux ? Ce qui semble très probable :-) ...
Peut-être qu'il serait possible d'utiliser en renfort les groupes qui partent tous de 2 :
-
Attention, Legendre et Gauss n'ont rien démontré à propos de la répartition des nombres premiers, tout au plus ils ont conjecturé le théorème des nombres premiers. La démonstration d'Erdös et Selberg est élémentaire au sens où elle n'utilise pas d'analyse complexe, mais elle est loin d'être facile ou éclairante. La voie royale est celle qui a été lancée par Riemann avec l'étude de sa fonction zêta, et achevée par Hadamard et de la Vallée-Poussin à la fin du XIXème siècle, en passant par l'analyse complexe.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.2K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 65 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 314 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres





