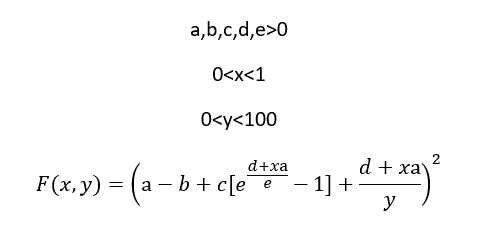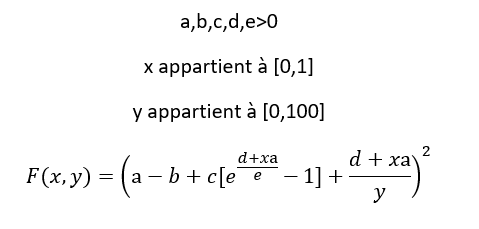Optimisation d'une fonction à deux variables

Cette question a plus sa place en analyse, mais déjà une remarque : $z\mapsto (a-b+z)^2$ est strictement croissante, donc le minimum de $F$ est atteint exactement là où celui de $G(x,y) = c(\exp(\frac{d+xa}{e} -1) + \frac{d+xa}{y}$ l'est

(je note $\exp$ puisque tu as aussi un paramètre $e$ qui traîne !)

Cette simplification étant faite, tu as désormais plusieurs manières de procéder, j'en vois au moins 3 (les deux premières sont les mêmes mais en inversant le rôle de $x$ et $y$) :

1- Tu fixes $y$ dans ton domaine, et tu minimises selon $x$, en étudiant la dérivée selon $x$. Tu calcules alors explicitement le minimum, qui est une fonction $K(y)$ : on minimise alors $K$.

2- tu fais pareil, dans l'autre sens

3- si tu connais ces choses-là (moins élémentaire que 1 et 2), tu peux aussi étudier le gradient de $G$ directement

(la méthode 1 marche pour la raison suivante : Soit $(x_0,y_0)$ obtenu par la méthode $1$ et $(x,y)$ un autre couple. Alors par définition, $K(y_0)\leq K(y)$, donc $G(x_0,y_0) = K(y_0) \leq K(y) \leq G(x,y)$ - tout ceci bien sûr en admettant que la fonction en question ait un minimum)

Le problème c'est que tu ne pourras pas minimiser: à $y$ fixé, c'est strictement croissant en $x$, donc si tu interdis la valeur $x=0$, tu ne peux pas minimiser. Pareil, à $x$ fixé, c'est strictement décroissant en $y$ donc si tu n'autorises pas $y=100$ tu ne pourras pas minimiser

D'accord, si tu prends les intervalles fermés c'est plus simple : regarde de près la formule qui définit $F$.

Fixons un $x$ quelconque dans $[0,1]$. Alors, lorsque $y$ grandit, $\frac{d+xa}{y}$ diminue, et le reste ne bouge pas. Mettre un carré, c'est croissant, donc à $x$ fixé, plus $y$ grandit, plus $F(x,y)$ diminue.

Du coup, si je veux minimiser, quoiqu'il arrive je devrai prendre $y=100$ (si le minimum est atteint en $(x,y)$ disons, alors la valeur est plus petite en $(x,100)$, d'après ce que je viens de dire)

Maintenant on peut donc fixer $y$ à $100$. Faisons la même analyse, mais avec $x$ : lorsque $x$ est de plus en plus petit, $d+xa$ est aussi de plus en plus petit (car $a>0$), et de même $\exp(\frac{d+xa}{e})$ est de plus en plus petit aussi.

A nouveau, le reste ne bouge pas, donc, ayant fixé $y$ à $100$, plus $x$ est petit, plus $F(x,100)$ est petit. Ainsi, si je veux atteindre le minimum, je dois prendre $x=0$ (pour la même raison : si le minimum est atteint en $(x,100)$, alors c'est plus petit en $(0,100)$)

Ainsi, le minimum est atteint lorsque $x=0, y = 100$.