Théorème point fixe de Brouwer
dans Analyse
Bonjour à tous, je consulte une preuve du théorème du point fixe de Brouwer (issue du Gonnord Tosel - Calcul différentiel, mais je n'arrive pas à mettre la main sur ce livre). La preuve me va bien, mais il y a un paragraphe qui comporte deux passages très énigmatiques pour moi, et j'ai beau me retourner la tête dans tous les sens je ne comprend pas. Je joins la preuve en pièce jointe.
Ma question :
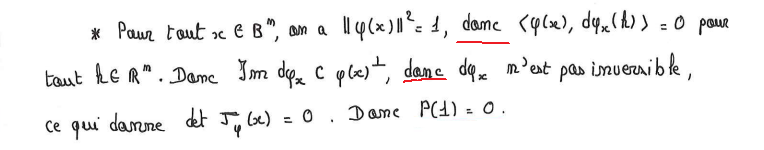
Comment justifier les deux implications soulignées en rouges ? Pour la première, je me dis que c'est quelque chose qui vient du fait que le gradient soit orthogonal aux lignes de niveau, et qu'on est justement sur une ligne de niveau (de valeur 1) de $\phi$, mais cela ne me satisfait pas beaucoup. Pour le deuxième point, alors là c'est le vide total car je ne comprends pas le rapport entre les deux assertions.
Merci de votre temps,
bien cordialement
Thibault.
Ma question :
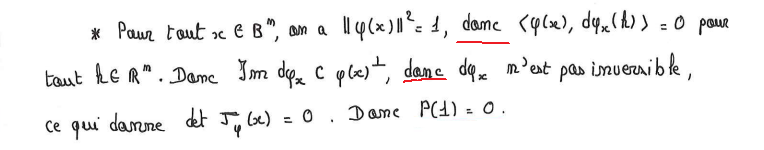
Comment justifier les deux implications soulignées en rouges ? Pour la première, je me dis que c'est quelque chose qui vient du fait que le gradient soit orthogonal aux lignes de niveau, et qu'on est justement sur une ligne de niveau (de valeur 1) de $\phi$, mais cela ne me satisfait pas beaucoup. Pour le deuxième point, alors là c'est le vide total car je ne comprends pas le rapport entre les deux assertions.
Merci de votre temps,
bien cordialement
Thibault.
Réponses
-
Premier point : $a(x):=|| \phi(x) ||^2 = <\phi(x),\phi(x)> = 1$. C'est la composée d'une forme bilinéaire et de $\phi$, c'est du cours que de savoir différencier cette expression (et sinon ça reste facile): $da(x)(k) = 2<\phi(x), d\phi(x)(k)>$. En différenciant la fonction constante $a=1$ on obtient $da(x)(k) = 0$ pour tout $k$. D'où le résultat.
Deuxième point : $\phi(x)$ n'est jamais nulle. Que peut-on dire d'une application linéaire (en l'occurence $d\phi(x)$) qui est toujours dans l'orthogonal d'un vecteur non nul ? Elle est non inversible, car la dimension de son image est inférieure ou égale à la dimension de l'orthogonal, qui est strictement plus petite que la dimension de l'espace puisque le vecteur $\phi(x)$ est non nul.
Plus directement, si $d\phi(x)$ était inversible, alors il existerait $k$ tel que $d\phi(x)(k) = \phi(x)$, et alors $0 = <\phi(x),d\phi(x)(k)> \,= || \phi(x) ||^2 = 1$ ce qui est absurde.
Attends que quelqu'un confirme ou infirme ce que j'écris, c'est lundi matin et j'ai jamais regardé Brower en détail. -
Bonjour Chalk, merci pout ta réponse qui m'éclaire.
J'ai une seconde question, plus de l'ordre de la visualisation. On pose le polynôme en t $P$, et on pose une intégrale comme ceci.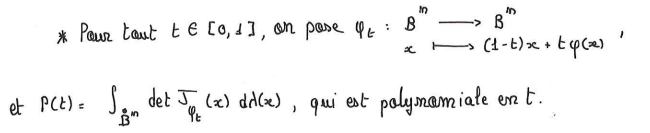
La contradiction vient du fait que cette intégrale vaut la mesure de l'intérieur de la boule unité, est constante en t et vaut 0.
Je n'arrive pas à visualiser à quoi correspond le $\lambda (x)$, est ce la mesure de Lebesgue sur $R^n$ ou le $\lambda$ plus haut dans la preuve?
Egalement, en haut de la dernière page, on a le calcul du jacobien, polynôme en t. On obtient naturellement une formulation comme ceci, mais je ne comprend pas pourquoi le $a_0$ s'est transformé en 1...
merci de votre aide!
cordialement,
Thibault -
Oui c'est la mesure de Lebesgue, et on a $a_0 = P(0)$.
-
Je ne vois toujours pas :
\begin{align*}
a_0&=P(0) = \int_B \det(J_{\phi_0}) d\lambda(x)= \int_B \det(J_{Id}) d\lambda(x) &\text{et donc}\\
a_0 &=\int_B \det(Id) d\lambda(x)=\int_B 1 d\lambda(x).
\end{align*} Ou serait mon erreur ? -
C'est une erreur du document alors, mais ça ne change pas la suite de la démonstration, en prenant $t$ suffisamment petit on a bien $\det J_{\varphi_t}(x) > 0$.
-
Merci beaucoup pour les explications

-
Les points clé sont:
"... est polynomiale en $t$..." (1)
"... changement de variable ça donne le volume de la boule..." (2)
(3)
" ... surjective pour $t$ assez petit..."
Les calculs sont là pour donner des garanties officielles, mais quasiment tout est visuel sauf le changement de variable et (1) qui sont des affaires formelles.
Je te prouve que pour $t$ assez petit, c'est surjectif. Soit $a\in B$ (forcément à l'intérieur de la boule).
Tu regardes le segment qui part de $a$ et qui va à son image par $\phi$. Tu prends un disque perpendiculaire à la droite portée par ce segment un peu en dessous de $a$. A un point $x$ de ce disque, tu associes d'abord le point $y:=\phi(x)$. Puis tu regardes où la droite passant par $y$ et $a$ va rencontrer le disque tu appelles ça $f(x)$. C'est picardien, il existe donc $x=f(x)$. Autrement dit quand tu vas de $x$ à $\phi(x)$, tu passes par $a$.
Bon évidemment, je t'ai pas fatigué (et ne me suis pas fatigué) à tordre le disque pour obtenir $\phi_t(x)=a$, mais tu vois la picarderie mobilisée dans le phénomène.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
J'appelle "picarderies" les applications du théorème de Picard qui donne des points fixes uniques à certaines "bonnes fonctions".Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres





