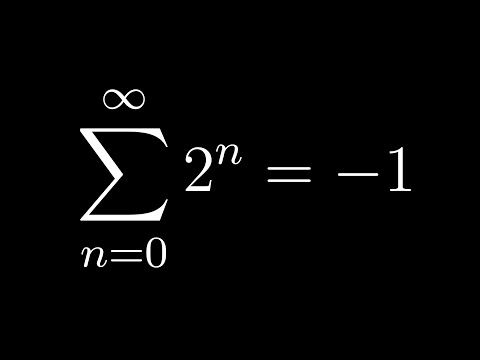1=0.999...+ presque rien.
Réponses
-
Oui c'est bien connu ! 0.999... = 1
Si tu fais tendre n vers l'infini c'est ce que tu obtiens
-
Selon toi noobey
$1\neq\frac{1}{10^n}+\sum_{i \mathop =1}^n \frac{9}{10^i}$
$1=\sum_{i \mathop =1}^n \frac{9}{10^i}$ -
Sais-tu ce que veut dire que deux nombres réels sont égaux ?
-
Non
-
En tout cas, les spams de robots vont se combiner pour t'arroser de nouvelles très diverses :-DAide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Dans ce cas pourquoi poses-tu une question sur des choses que tu ne connais pas ?
-
christophe c
J'ai pas compris ce que tu voulais dire.
Poirot
Dans ce cas pourquoi poses-tu une question sur des choses que tu ne connais pas ?
Parce que je ne me pose pas de question sur les choses que je connais.
Excuse moi pour la réponse, faut avouer que la question était un peu masochiste. -
Ce qu'il veut dire par là, c'est que c'est comme si je demandais pourquoi les zefzfoioj sont toujours gnrege, alors que je ne connais ni la définition de zefzfoioj ni celle de gnrege.
Tu te poses une question sur des objets que tu ne connais pas à part leur nom. La réponse n'a donc aucun intérêt. -
Je parlais de ton astucieux pseudo destiné à te faire plein de potes.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Je n'ai pas bien saisi l'histoire des salles.
A revisionner.
La question légitime est quel est le sens et l'utilité de ces nombres 1/2,-1 ou bien -1/12 ? -
L'idée de l'histoire des salles est de montrer une équivalence de principe.
Si on part de l'idée que $1+2+4+8+16...=-1$
On a successivement $1=1$ , $1+2=3$ , $1+2+4=7$, .... et donc la suite $1,3,7,15....$ doit tendre vers $-1$.
Comme $2^0+2^1+2^2+...+2^n=2^{n+1}-1$ cela équivaut à dire que $2^{n+1}$ tend vers 0.
Les salles sont une image de ces affinements successifs (il s'arrête à 16 pour la visibilité, mais il faut voir ça dans le cadre d'une découpe infinie). En gros, il découpe ces affinements en salles, sous-salles, sous-sous-salles en gardant les $2^n$ successifs dans les mêmes (sous) salles que 0, et en faisant tendre ceux-ci vers 0 (pour l'exemple 16 et 0 sont superposés). Ensuite il utilise le principe de shift-invariant (la distance entre 0 et 2 est la même qu'entre 1 et 3...) pour positionner les autres nombres. Il abouti à une image qui montre qu'en remontant 1->3->7->15... on tend vers -1.
$\frac{-1}{12}$ est bien connu des amateurs de Ramanujan et de Riemann. Par contre, ici je vois les même "erreurs" que Ramanujan faisait dans certaines de ses suites: on additionne des séries/ensembles qui n'ont pas la même longueur/densité asymptotique, et on remplace rapidement le terme le plus important par "...", ce qui donne des résultats surprenants.
Ici en l'occurence, on part de l'idée d'une découpe de l'interval [0-1] avec l'équation $(1-p)+p(1-p)+p^2(1-p)+p^3(1-p)+p^4=1$ que l'on prolonge à l'infini, sauf que le dernier terme (ici $p^4$) devrait non seulement empêcher qu'on puisse simplifier en $1+p+p^2+p^3+...=\frac{1}{1-p}$, mais en plus c'est lui qui annule tous les autres pour donner une constante (si on développe l'équation de départ on a en réalité $1-p^4+p^4=1$). Prendre des valeurs de $p$ qui sortent de l'interval dans lequel la fonction à été définie est certes intéressant, mais à faire avec précaution, surtout si au lieu de devenir négligeables (...), les termes successifs prennent de l'ampleur.
La convergence, divergence, semi-divergence joue un rôle important (voir par ex le théorème de réarrangement de Riemann). L'addition n'est pas définie pour des sommations infinies. Si on change l'ordre des termes, cela peut donner des résultats différents (exit la commutativité). Si le résultat est confirmé par d'autres méthodes (Abel, Cezaro...) alors il est peut-être utilisable (comme c'est le cas pour $\frac{-1}{12}$). -
"Si j’enlève presque rien 1 est il toujours égal a 0,999...?"
Jamais
"Presque rien" n'étant pas "rien", donc non nul, en l'ôtant de 1 on obtient un nombre inférieur à 0,999... -
une découpe de l'interval [0-1] avec l'équation
$(1-p)+p(1-p)+p^2(1-p)+p^3(1-p)+p^4 = 1$
$1+p+p^2+p^3+...+\frac{p^n}{1-p} = \frac{1}{1-p}$
$\frac{p^n}{1-p}+1+\sum_{i \mathop =1}^n p^n = \frac{1}{1-p}$
une découpe de l'interval [0-n] avec l'équation
$(n-p)+p(n-p)+p^2(n-p)+p^3(n-p)+p^4 = n$
$1+p+p^2+p^3+...+\frac{p^n}{n-p} = \frac{n}{n-p}$
$\frac{p^n}{n-p}+1+\sum_{i \mathop =1}^n p^n = \frac{n}{n-p}$
$\frac{p^n}{n-p}+\frac{n-p}{n-p}+\frac{\sum_{i \mathop =1}^n (n-p)p^n}{n-p} = \frac{n}{n-p}$
$p^n+n-p+\sum_{i \mathop =1}^n (n-p)p^n = n$
:)o -
Ce serait plutôt ceci:
$(n-np)+p(n-np)+p^2(n-np)+....+np^n=n$
$1+p+p^2+....+\frac{np^n}{n-np}=\frac{n}{n-np}$
$\frac{np^n}{n-np}+\frac{n-np}{n-np}+\frac{\sum_{i \mathop =1}^{n-1}(n-np)p^i}{n-np} = \frac{n}{n-np}$
$np^n+n-np+\sum_{i \mathop =1}^{n-1} (n-np)p^i = n$ -
Pourquoi tout ce fatras pour éviter l'essentiel?
Certains nombres réels n'ont pas d'écriture décimale unique comme le nombre $1$.
La non unicité d'écriture n'est pas une nouveauté.
Quand on écrit un nombre rationnel sous forme de fraction $\frac{a}{b}$ avec $a,b$ des entiers et $b$ non nuls, cette écriture n'est pas unique. -
Et c'est quand même dommage de laisse ce titre faux ! Il n'y a pas de "presque".
L'auteur de ce fil est un spécialiste des questions sans signification. -
ou encore $1=3*\frac{1}{3}=3*0,3333333...=0,999999...$
-
$1=3*\frac{1}{3}=\frac{1}{10^n}+3*0,3333333...=\frac{1}{10^n}+0,999999...$
$1=\frac{1}{10^n}+3\sum_{i \mathop =1}^n \frac{3}{10^i}$
1/3 fini
0,333...infini.
$\pi$ fini
3.141159 infini
$\sqrt 2$ fini
1,414213562 infini
A l'infini il manque toujours un petit quelque chose pour être égal a un nombre fini comme $\pi$ ,$\sqrt 2$,1/3
La je sent que les injures vont se transformer incantations me suppliant d'avouer que je suis stupide puis de m'excuser jute avant de me suicider une infinité de fois. X:-( -
Qui est $n$ dans ta première ligne ?
Oui, tu es spécialiste des messages sans signification mathématique, ou carrément faux. Ce n'est pas une injure, c'est juste une constatation. -
l'infini.
-
Thomas:
Tu n'arrives pas à imaginer/visualiser $0,999999...$ c'est à dire un zéro suivi d'une infinité de neuf.?
$0,9999999999$ et $0,999999999999...$ ne sont pas des nombres égaux.
Si tu écris $0,$ suivi d'un nombre fini de $9$ le nombre que tu obtiens ainsi n'est pas égal à $0,9999...$ les trois petits points indiquent qu'on écrit $9$ sans fin.
Le nombre:
$0,9999999999999999999999999999999999999999999999999999999999999999999999999999999$
n'est pas égal non plus à:
$0,9999999...$ -
La question de départ n'est, selon moi, pas sans intérêt. L'infini en mathématique n'est pas un sujet léger (infini dénombrable où pas, ordinaux, et même les opérations de base qui ne sont pas complètement définies sur l'infini).
La question est déjà dans le deuxième post:
$1=\frac{1}{10^n}+\sum_{i \mathop =1}^n \frac{9}{10^i}$ est valable pour tout $n$, pas pour n infini?
$1=\sum_{i \mathop =1}^n \frac{9}{10^i}$ est valable pour $n$ infini...réellement?
Les puristes diront même qu'une somme qui tend vers une valeur réelle, c'est en réalité la plus grande valeur réelle possible inférieur à la valeur à laquelle elle tend.
D'ailleurs la réponse se trouve partiellement dans ce constat: Comme le dernier terme de la somme infinie est censé amener la somme vers le plus grand réel inférieur à 1 (donc il n'existe rien entre la somme et le réel 1), il y a une incompatibilité avec le fait que $\frac{1}{10^\infty}$ soit encore plus petit que ce dernier $\frac{9}{10^\infty}$.
Chercher à comprendre toutes les subtilités de l'infini n'est pas "idiot" -
$n$ est un nombre entier naturel. Ce que tu appelles "infini" n'est pas un nombre entier.
$1-0.9999...=0$
Les trois petits points indiquent qu'on écrit sans fin le chiffre $9$
PS:
Le nombre obtenu en écrivant $0,$ suivi d'un milliard de fois le chiffre $9$ n'est pas égal à $0,999...$. -
C'est pour cette raison qu'on utilise $\lim_{n\to\infty}$, qui est implicite quand on écrit $\sum^{+\infty}$, mais pour moi c'était clairement sous-entendu. $1^\infty$ est indéterminé, mais ce n'est pas le cas des autres réels, donc il y a matière à réflexion.
-
Je suis curieux de voir quel sens tu donnes à $(-1)^\infty$ puisqu'il parait que $x^\infty$ est un nombre réel bien déterminé si $x\neq 1$ selon toi.
Il n'y a pas d'entier "infini" quoique tu en dises.
La suite définie pour tout entier naturel non nul par, $u_n=1-10^{-n}$ converge bien vers $1$ mais aucun élément de cette suite n'est égal à $1$. -
$1=\frac{1}{10^n}+\sum_{i \mathop =1}^n \frac{9}{10^i}$ pour tout n et meme pour l'infini.
$1=\sum_{i \mathop =1}^n \frac{9}{10^i}$ uniquement pour l'infini.
Pour faire une analogie la loi de newton fonctionne bien sur terre celle d’Einstein fonctionne sur terre et même pour notre galaxie.
Pourquoi se passer des détailles en mathématique? -
Thomas:
C'est toi qui te passe des détails. -
Attention, je parle toujours dans le cadre de $\lim$, il faut le voir comme $\lim_{n\to\infty}x^n$. C'est bien ce $\lim$ qui permet d'utiliser des égalités là où il n'y en a pas. On ne peut pas réellement dire que le plus grand réel inférieur à la limite soit égal à cette limite si on ne le traite pas comme tel.
-
$\lim_{n \to +\infty}\sum_{i \mathop =1}^n \frac{9}{10^i}=1$
$\sum_{i \mathop =1}^n \frac{9}{10^i}=1-\frac{1}{10^n}$
A votre guise. -
Hehe...et maintenant si on utilisait $n=\omega-1$...
-
Excuse moi, je ne suis pas mathématicien c'est quoi $n=\omega-1$?
-
Tous les naturels sont finis. $\omega$ est le premier ordinal transfini (infini). Donc on peut dire qu'un naturel qui tend vers l'infini, tend vers $\omega$. A priori, le "dernier naturel" pourrait théoriquement s'écrire de cette manière (à prendre avec des pincettes car pour tout $n$ on peut toujours trouver un $n+1$ inférieur à $\omega$). Et si on continue le raisonnement, on pourrait remplacer la $\lim_{n\to\infty}$ par $n=\omega-1$
-
Pour faire plaisir a Fin de partie tous les 0.999...ne se valent pas.
$0,1-\frac{1}{10^{n+1}}+\sum_{i \mathop =1}^n \frac{8,1}{10^i}=\sum_{i \mathop =1}^n \frac{9}{10^i}\neq-9+\sum_{i \mathop =0}^n \frac{9}{10^i}$
Je ne suis pas sectaire. -
Collag3n:
Tu n'as pas répondu réellement à ma question.
Tu as affirmé quelques messages plus haut que "$x^\infty$ était bien défini pour tout réel $x$ sauf pour $x=1$.
J'aimerais savoir à quel réel correspond l'écriture $(-1)^\infty$.
Je pose cette question car la suite définie pour tout $n$ entier naturel non nul par $(-1)^n$ n'a pas de limite.
Par contre, la suite définie pour tout $n$ entier naturel non nul, par $1^n$ elle, a bien une limite, $1$.
Il n'y a pas de plus grand entier dans l'ensemble des entiers naturels et cet ensemble n'a pas un nombre fini d'éléments.
Pire, il n'y a pas non plus de réel $x$ qui soit tel que pour tout $n$ entier $n\leq x$
L'ensemble des rationnels inférieurs ou égaux à $\sqrt{2}$ n'a pas de plus grand élément.
Si $r$ est un rationnel tel que $r\leq \sqrt{2}$ il existe toujours un rationnel $r'>r$ tel que $r'\leq \sqrt{2}$ -
Pourtant cette dernière équation est une pure égalité, même si on la prend à la $\lim$....
-
Pour tout $n$ entier naturel non nul,
$\displaystyle \sum_{k=1}^n \left(9\times 10^{-n}\right)\neq 0,99999...$ -
Collag3n:
La suite $(-1)^n$ n'a pas de limite.
Pour $n$ pair on a, $(-1)^n=1$ et pour $n$ impair on a $(-1)^n=-1$. Cela permet d'affirmer que cette suite n'a pas de limite.
Le résultat classique pour la suite $(x^n)$ est le suivant:
Cette suite converge comme suite de réels si et seulement si:
$-1<x\leq 1$ -
Fin de partie
Sorry, je n'avais pas vu ton signe "-". Mon point était juste de dire que l'utilisation que thomas en faisait était tout à fait valable.
Pour le reste, c'est pour ça que j'ai précisé "avec des pincettes car on peut toujours trouver un $n+1$ inférieur à $\omega$". $\omega$ est purement théorique, et donc en théorie on pourrait très bien définir $\omega-1$. Comme $\omega$ est le premier ordinal infini, que serait donc $\omega-1$? -
Collag3n,
ce que tu racontes ici est assez inquiétant ! le "théorique" a bon dos !
" en théorie on pourrait très bien définir $\omega -1$". Mais voyons-donc ! Si $\omega$ est un ordinal, ça n'a pas de sens. Mais peut-être parles-tu de ce que tu ne connais pas !
Par contre, en termes de cardinaux, $\omega -1=\omega$.
Et précédemment, ton passage "le "dernier naturel" pourrait théoriquement ..." est du baratin de bonimenteur de foire, puisque tu parles de ce qui n'existe pas (exactement comme la qualité extraordinaire du produit vendu par le bonimenteur).
Pourquoi rajouter aux questions non mathématiques de G.. des baratins de cet ordre ? Du coup, tu passes toi aussi pour un incompétent. -
si l’équation n'est pas égale pour "n" entier naturel pourquoi serait elle a l'infini?
cendrillon a minuit tu rentre dans ta citrouille et tu laisse une chaussure. -
Un peut hors sujet.
$a=\frac{2sin\frac{2\pi n}{3}}{\sqrt{3}}=0,+1,-1,...$
$b=\frac{4cos(\frac{2\pi n}{3})-1}{3}=+1,-1,-1,...$
Construction de t, u, v plus pratique a manipuler.
$t=a^2+ab+a+b=;1,0,0;...$
$u=\frac{1-a^2-ab-b}{2}=;0,1,0;...$
$v=\frac{a^2+ab+2a+b-1}{-2}=;0,0,1;...$
Remarque amusante t+u+v=1 peut importe la valeur de n. -
Thomas a écrit:si l’équation n'est pas égale pour "n" entier naturel pourquoi serait elle a l'infini?
l'infini n'est pas un entier donc l'équation dont tu parles n'est pas vérifiée à proprement parler pour l'infini.
On a bien,
$1=\sum_{n=1}^{\infty} 9\times 10^{-n}$
Mais visiblement tu ne comprends pas la signification de cette égalité, le concept de limite.
Cette écriture est équivalente à dire que la suite des nombres décimaux $0,9;0,99;0,999;0,9999;0,99999;$ etc
tend vers $1$ et aucun de ces nombres n'est égal à $1$. -
zap
-
Collag3n:
On fait beaucoup d'abus de notation en mathématiques mais ceux qui le font pensent s'adresser à des gens qui ont suffisamment de discernement pour reconnaître ces abus. La notation $\sqrt{-1}$ est un de ces abus parmi d'autres.
PS:
Puisque $i^2=(-1)^2$ alors il est clair que $\sqrt{-1}$ ne peut pas désigner sans confusion possible un nombre. -
Je suis tout a fait capable de répéter se que tu me dis Fin de partie.
Quoi qu'il en soit je ne pense pas qu'il y ai de découverte révolutionnaire a faire a part débattre.
Bon sur ce bonne nuit. -
Fin de partie
j'ai zappé. Même jouer avec des "choses qui n'existent pas" à plus de sens pour moi que de répondre à ce que la nature humaine s'évertue à faire exister.... -
Je pense qu'il est temps de fermer ce fil sans queue ni tête.
Cette discussion a été fermée.
Bonjour!
Catégories
- 163.2K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 65 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 69 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 314 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres