L'indéterminisme dans les suites de Collatz
Salut à tous,
Voici les réflexions auxquelles m'ont conduites mes recherches sur les suites de Collatz, ou problème $3n+1$. Je commencerai par quelques définitions :
Dans l'extrait de suite descendante $...,p,n,...$ on déduit la valeur de $n$ de celle de $p$ :
$n=\displaystyle\frac{3\,p+1}{2^u}$
Ce calcul ne présente aucune difficulté, sinon celle de connaître $u$, que l'on contourne en divisant $u$ fois le numérateur par 2.
Toujours dans la même suite, mais dans le sens ascendant, on peut calculer $p$ lorsqu'on connaît $n$ :
$p=\displaystyle\frac{2^u\,n-1}{3}$
Mais le même problème se pose : quelle est la valeur de $u$ ? Par quelle puissance de 2 doit-on multiplier $n$ pour qu'une fois le résultat décrémenté il soit divisible par 3 ? On règle ce problème en précisant ce qu'est $u$ :
$u=2\,r-m+1$, où
$n=\displaystyle\frac{3\,p+1}{\color{red}2^\color{red}u}\:,\:p=\displaystyle\frac{2^{2\,r-m+1}\,n-1}{3}$
J'ai remplacé ${2\,r-m+1}$ au dénominateur par $2^u$, suite à la remarque que je fais plus bas dans une de mes réponses.
Reprenons l'exemple de $n=31$ et voyons comment on calcule son prédécesseur $p$. On sait que $m=1$, mais pour ce qui est de $r$ sa valeur relève de notre choix. Prenons $4$ :
$2645=\displaystyle\frac{2^{2\times4-1+1}\times31-1}{3}$
Si nous avions voulu obtenir le plus petit prédécesseur de $31$ nous aurions choisi $r=1$ :
$41=\displaystyle\frac{2^{2\times1-1+1}\times31-1}{3}$
Dans le sens descendant les choses sont plus compliquées, car nous ne savons rien de
$m=1\,:\,u=2\,r-1+1=2\,r\:\rightarrow\,\text{u pair}$
$m=2\,:\,u=2\,r-2+1=2\,r-1\:\rightarrow\,\text{u impair}$
La parité de $u$ étant fonction du modulo 3 de $n$, elle nous renseigne sur la valeur de $m$. Lorsqu'on pose
$31=\displaystyle\frac{3\times2645+1}{2^8}\:,\:35=\displaystyle\frac{3\times373+1}{2^5}$
on sait que dans le premier cas $m=1\:\text{et}\:r=8/2=4$, et que dans le second cas $m=2\:\text{et}\:r=(5+1)/2=3$. Les prédécesseurs de $35$, dont le modulo 3 est 2, sont en effet $23,93,373,...$
En résumé,
PS : ceux qui désirent savoir d'où sort $u=2\,r-m+1$ peuvent consulter mon document mis à jour aujourd'hui à partir du bas de la page 6.
Voici les réflexions auxquelles m'ont conduites mes recherches sur les suites de Collatz, ou problème $3n+1$. Je commencerai par quelques définitions :
- Par "suite de Collatz" j'entends une suite ne comprenant que ses termes impairs. Elle est construite à l'aide de l'algorithme éponyme condensé.
- Une suite descendante est construite à partir de son premier terme, tandis qu'une suite ascendante l'est à partir du dernier.
- Plutôt que d'utiliser la notation $n_{i-1}, n_i$ je préfère utiliser $p,n$, le premier étant le prédécesseur du second.
Dans l'extrait de suite descendante $...,p,n,...$ on déduit la valeur de $n$ de celle de $p$ :
$n=\displaystyle\frac{3\,p+1}{2^u}$
Ce calcul ne présente aucune difficulté, sinon celle de connaître $u$, que l'on contourne en divisant $u$ fois le numérateur par 2.
Toujours dans la même suite, mais dans le sens ascendant, on peut calculer $p$ lorsqu'on connaît $n$ :
$p=\displaystyle\frac{2^u\,n-1}{3}$
Mais le même problème se pose : quelle est la valeur de $u$ ? Par quelle puissance de 2 doit-on multiplier $n$ pour qu'une fois le résultat décrémenté il soit divisible par 3 ? On règle ce problème en précisant ce qu'est $u$ :
$u=2\,r-m+1$, où
- $m=n\:mod\:3$.
- $r$ est le rang (ou indice) de $p$ dans la suite des prédécesseurs de $n$. Avec $n=31$, par exemple, $r=4$ lorsque $p=2645$, car les prédécesseurs de $31$ sont $41, 165, 661, 2645, ...$
$n=\displaystyle\frac{3\,p+1}{\color{red}2^\color{red}u}\:,\:p=\displaystyle\frac{2^{2\,r-m+1}\,n-1}{3}$
J'ai remplacé ${2\,r-m+1}$ au dénominateur par $2^u$, suite à la remarque que je fais plus bas dans une de mes réponses.
Reprenons l'exemple de $n=31$ et voyons comment on calcule son prédécesseur $p$. On sait que $m=1$, mais pour ce qui est de $r$ sa valeur relève de notre choix. Prenons $4$ :
$2645=\displaystyle\frac{2^{2\times4-1+1}\times31-1}{3}$
Si nous avions voulu obtenir le plus petit prédécesseur de $31$ nous aurions choisi $r=1$ :
$41=\displaystyle\frac{2^{2\times1-1+1}\times31-1}{3}$
Dans le sens descendant les choses sont plus compliquées, car nous ne savons rien de
- $m$ puisqu'il est une propriété de $n$, non encore calculé.
- $r$ puisque le rang de $p$ dans la suite des prédécesseurs de $n$ n'est pas connu.
$m=1\,:\,u=2\,r-1+1=2\,r\:\rightarrow\,\text{u pair}$
$m=2\,:\,u=2\,r-2+1=2\,r-1\:\rightarrow\,\text{u impair}$
La parité de $u$ étant fonction du modulo 3 de $n$, elle nous renseigne sur la valeur de $m$. Lorsqu'on pose
$31=\displaystyle\frac{3\times2645+1}{2^8}\:,\:35=\displaystyle\frac{3\times373+1}{2^5}$
on sait que dans le premier cas $m=1\:\text{et}\:r=8/2=4$, et que dans le second cas $m=2\:\text{et}\:r=(5+1)/2=3$. Les prédécesseurs de $35$, dont le modulo 3 est 2, sont en effet $23,93,373,...$
En résumé,
- Dans le sens ascendant, $m$ est connu puisque $n$ l'est. Mais la valeur de $r$ est arbitrairement fixée à chaque étape, et on ne peut pas privilégier une valeur quelconque puisque aucune ne donnera de sens particulier au résultat. Cette variable interdit toute possibilité d'atteindre une valeur préalablement choisie de $n$ après un certain nombre d'étapes.
- Dans le sens descendant, les valeurs respectives de $m$ et de $r$ sont déterministes, liées uniquement au nombre de fois qu'on a pu diviser $3\,p+1$ par 2.
PS : ceux qui désirent savoir d'où sort $u=2\,r-m+1$ peuvent consulter mon document mis à jour aujourd'hui à partir du bas de la page 6.
Réponses
-
Bonjour,
je ne comprends pas le raisonnement lié au donc de cette phrase, la dernière de ton message :
Or, personne à ma connaissance n'a jamais constaté le moindre schéma ou cycle dans la succession des valeurs de u. La construction d'une suite de Collatz est donc bien un processus déterministe dans le sens descendant, et stochastique dans le sens ascendant.
Mais peut-être qu'il me faudrait une définition claire de "déterministe" ou "stochastique" (c'est à moi de bosser dessus).
La question que je te pose : ton "donc" est-il un raisonnement ou une conjecture ? Ou bien tout simplement, est-ce une lapalissade si on applique les définitions de "déterministe" et "stochastique". -
Bonjour,
Tu observes que tous les entiers de la forme $2^a(2b+1)$ avec $a,b$ entiers possèdent le même successeur dans la suite de Collatz condensée : $2b+1.$ Et tu observes que si on se donne seulement $2b+1$, on ne sait rien sur $a.$
Tu fais bien de poster dans Shtam.
Par ailleurs, aujourd’hui est un mardi. Quel jour suis-je né ? Il n’y a rien de stochastique, ni d’aléatoire, car le jour de ma naissance est parfaitement déterminé. Je t’encourage à relire ton poste : quel est l’aléa dont tu parles ? -
@Dom,
Je t'accorde que la formulation est un peu ambigüe. Ce que j'ai voulu dire est que lorsqu'on observe la succession des exposants de 2 dans une suite impaire de Collatz, on ne trouve aucune régularité, aucun cycle. Du point de vue de l'analyse qu'on peut en faire, la valeur des exposants est totalement aléatoire, donc celle des valeurs successives de $r$. D'un point de vue strictement arithmétique, il est évident que la valeur d'aucun exposant n'est due au hasard, mais résulte d'une manière ou d'une autre de celui qui le précède, d'où le terme de "processus déterministe". Ça c'était pour le cas d'une suite descendante.
Dans le cas d'une suite ascendante, la valeur du prédécesseur de $n$ résulte du choix de $r$, qui est aléatoire dans le sens où le choix de telle ou telle valeur ne fait aucune différence. On effectuerait un choix raisonné si son résultat, ou plutôt le résultat de choix raisonnés successifs, permettaient de créer une suite du type particulier qu'on recherche, quel qu'il soit (mais pour ça je suppose qu'il faudrait faire intervenir une variable cachée). Le hasard intervient donc dans la construction d'une suite ascendante, ce qui correspond à la définition du concept de processus stochastique : "Qui est au moins partiellement dû au hasard, qui contient une variable aléatoire".
@YvesM,
"quel est l’aléa dont tu parles"
Je viens de l'expliquer. J'espère l'avoir fait plus clairement que dans mon post. -
Autrement dit, un père peut avoir plusieurs descendants mais un descendant n'a qu'un père. Ca fait penser à des trucs connus modulo l'inversion fils vs père et ascendant vs descendant. Rien de transcendant, mais c'est pas faux.
-
Un nombre qui se trouve à $k$ étapes de la racine $1$ s'écrit sous cette forme :
$n_k=\frac{2^{l_1+l_2+\cdots+l_k}}{3^k}-\frac{2^{l_2+l_3+\cdots+l_k}}{3^k}-\frac{2^{l_3+l_4+\cdots+l_k}}{3^{k-1}}-\frac{2^{l_4+l_5+\cdots+l_k}}{3^{k-2}}-\cdots-\frac{2^{l_{k-1}+l_k}}{3^3}-\frac{2^{l_k}}{3^2}-\frac{2^0}{3^1}$
Si on exclut les reformulations dues aux cycles (ex: $5 = \frac{2^4}{3} -\frac{1}{3} = \frac{2^6}{3^2} - \frac{2^4}{3^2} - \frac{1}{3} = \frac{2^8}{3^3} - \frac{2^6}{3^3} - \frac{2^4}{3^2} - \frac{1}{3}$), cette forme devrait être unique pour chaque $n$.
Prouver que tout $n$ peut s'écrire sous cette forme c'est prouver la conjecture.
Trouver une combinaison de $l_k$ qui donne un entier, c'est trouver son chemin. Le fait qu'il n'y ait pas encore de technique connue pour le faire, ne veut pas dire que ce soit aléatoire. -
depasse a écrit:Autrement dit, un père peut avoir plusieurs descendants mais un descendant n'a qu'un père.
Tout dépend du sens dans lequel tu te déplaces dans la suite, alors pour commencer il faudrait décider d'une terminologie afin d'éviter de nommer la même entité père dans un sens et fils dans l'autre. Puisque habituellement on se déplace dans le sens descendant, disons que $p$ est le père et $n$ le fils, ce qui cadre bien avec le concept de prédécesseur et de successeur. Dans le sens descendant le père $p$ n'a qu'un fils $n$. Dans le sens ascendant, le fils $n$ peut avoir avoir une infinité de pères $p$. Le gène qui permet de savoir lequel est vraiment le père est la variable aléatoire $r$. En choisissant de donner à $r$ telle valeur, tu sélectionnes tel père, ce choix faisant des autres $p$ des pères potentiels. Il n'y a par conséquent aucune contradiction : dans les deux sens on ne trouve à chaque étape qu'un père et un fils, la seule différence étant que dans le sens descendant le père vient avant le fils, et que dans le sens ascendant le fils vient avant le père (ou plutôt, on s'emploie à lui trouver un père).
Supposons qu'un fils veuille remonter jusqu'à son ancêtre très lointain (sens ascendant). Il peut le faire s'il est capable de construire son arbre généalogique, autrement dit s'il connaît sa filiation. Le fils $n$, pour sa part, ne peut pas remonter jusqu'à son ancêtre lointain $p_0$ parce qu'il ne connaît que son père. Il ne sait rien du - n'est pas concerné par - le choix aléatoire du gène $r$ qui fera que son grand-père sera tel ou tel à l'étape suivante. Les variables $n, m, p, r$ ne concernent qu'un seul couple père-fils, une seule étape dans la construction de la suite ascendante.
Vu depuis l'autre bout, dans le sens descendant, l'ancêtre $p_0$ n'est autre que le premier terme de la suite. Cet ancêtre lointain n'a eu qu'un seul fils, qui lui-même n'a eu qu'un seul fils, etc. On peut établir sa descendance d'autant plus facilement que le hasard n'y a joué aucun rôle.
Ce qui interdit toute possibilité de $re$construire une suite dans le sens ascendant (dont le sens descendant est connu), est donc le fait que chaque valeur de $n$, à chaque étape, possède une infinité de prédécesseurs potentiels $p$, et que la valeur de la variable aléatoire $r$ qui a sélectionné tel prédécesseur à telle étape, ne peut être connue que dans le sens descendant lorsqu'on extrait $r$ de $u$. D'ailleurs j'en profite pour revenir sur ce que j'ai écrit dans mon premier post, à savoir $n=\frac{3 p+1}{2^{2\,r-m+1}}$. En réalité il faut écrire
ascendant $\rightarrow\,p=\displaystyle\frac{2^{2\,r-m+1}\,n-1}{3}\:,\:$ descendant $\rightarrow\,n=\displaystyle\frac{3\,p+1}{2^u}$
car dans le sens descendant on ne peut connaître $m$ et $r$ qu'après avoir déterminé $u$ au moyen de divisions successives par 2.
@Collag3n,
Ce que tu énonces concerne le sens descendant. Le caractère aléatoire d'une suite n'existe que dans le sens ascendant. -
Ne pointes-tu pas le caractère surjectif et non injectif d'une application ?
En effet, quand tu choisis l'image de $\mathbb N$ par la fonction nulle, c'est difficile de retrouver le père de quelqu'un. -
La formule décrit le chemin qui sépare $n$ de $1$. Ce chemin est unique, que tu le parcours dans un sens ou dans l'autre. Rien ne dit qu'il n'existe pas un moyen de déterminer la formule uniquement sur base de $n$ (valeur de $n$ préalablement fixée comme tu dis), et donc de connaître son chemin exact. Par exemple, le premier terme est un exposant de 2 sur un exposant de 3 et est très proche de $n$
-
Collag3n a écrit:La formule décrit le chemin qui sépare n de 1. Ce chemin est unique, que tu le parcours dans un sens ou dans l'autre.
Prenons l'exemple de 7,11,17,13,5,1. Parcourir ce chemin signifie partir de 7, calculer 11, puis 17, etc. jusqu'à 1, ce qui est de l'arithmétique de base. Mais si décides de partir de 1 pour revenir à 7, alors deux cas se présentent : faire ce calcul en te basant sur la connaissance que tu as de ce chemin particulier, ou le faire sans en avoir la moindre connaissance. Lorsque tu dis que ce chemin est unique dans un sens ou dans l'autre, tu te places d'office dans le premier cas : tu sais qu'avant 1 il y a 5, qu'avant 5 il y a 13, etc. Si tu te places dans le second cas tu constateras que déjà tu n'as aucune idée du prédécesseur à attribuer à 1, tel qu'il te conduira à coup sûr jusqu'à 7. Et ce problème va se reproduire à chaque étape, l'erreur que tu pourrais commettre à l'une d'elles ayant pour conséquence inévitable de te faire rater ton objectif.
Alors tu décides d'utiliser la variable aléatoire $r$. Mais le constat est le même : quelle valeur lui attribuer dans le calcul du prédécesseur de 1 ? Supposons que tu tentes l'expérience avec 1, 2, ..., 9 : tu vas obtenir pour prédécesseurs potentiels 1, 5, 21, 85, 341, 1365, 5461, 21845, 87381. Mais ça t'avancera à quoi ?
Tu n'as strictement aucun moyen de reproduire le chemin descendant de 7 dans le sens ascendant, et ceci pour la raison que j'ai maintes fois évoquée, à savoir que dans le sens descendant chaque terme de la suite n'a qu'un seul successeur, alors que dans le sens ascendant il possède une infinité de prédécesseurs. Sans la connaissance du chemin descendant tu ne peux pas le parcourir dans le sens inverse, cette connaissance ayant trait à la valeur de $r$ utilisée à chaque étape.
Il faudrait éliminer le hasard en trouvant le moyen de calculer, non pas les termes de la suite ascendante mais les valeurs successives de $r$ qui les déterminent, parce que ce sont elles qui véritablement construisent cette suite. -
Oui, les valeurs successives des $r$ ou des $u$ (qui correspondent aux $l_k$ de la formule) déterminent la formule pour $n$. Mon point est que rien ne dit qu'il n'existe pas de technique qui permettent de trouver ces $l_k$ (ou les $r$) sur base de $n$ uniquement (et pas en tentant de partir de 1). En tout cas, cela n'a rien d'aléatoire. Maintenant je ne sais pas si ton point est plutôt de parler "en apparence aléatoire" (comme pour la distribution des nombres premier, qui est en apparence aléatoire, mais qui n'a absolument rien d'aléatoire).
-
Collag3n a écrit:Maintenant je ne sais pas si ton point est plutôt de parler "en apparence aléatoire" (comme pour la distribution des nombres premier, qui est en apparence aléatoire, mais qui n'a absolument rien d'aléatoire).
C'est un vaste débat, mais ce qui quelquefois cache notre ignorance est plutôt le formalisme probabiliste. Le caractère aléatoire d'un phénomène est d'une autre nature. Le problème qui nous occupe ici n'est pas apparenté à celui de la distribution des nombres premiers mais à l'obligation de faire des choix - même si on les délègue à une machine - sans connaissance de leurs conséquences. Lorsqu'on construit une suite descendante on le fait pour vérifier qu'elle atteint bien 1 ; lorsqu'on construit une suite ascendante on ne s'attend strictement à rien, on ne fait qu'aligner des nombres en quantité qui pourrait atteindre l'infini si la fatigue ne venait pas mettre un terme à cette occupation. Leur seul intérêt est d'avoir révélé le facteur $r$ qui était caché dans $u$, et de nous offrir un cadre dans lequel le manipuler (en plus de pouvoir calculer la suite des prédécesseurs de $n$, bien sûr). La question est de savoir ce qu'il est possible d'en tirer. -
Ce discours pseudo-probabiliste est stupéfiant.
-
Salut.Wilfrid a écrit:Lorsqu'on construit une suite descendante on le fait pour vérifier qu'elle atteint bien 1 ; lorsqu'on construit une suite ascendante on ne s'attend strictement à rien..
Je pense que lorsqu'on construit une suite ascendante partant de $1$, on devrait s'attendre à ce que ça atteigne tous les entiers. Si la conjecture est vraie, ceci est réalisé par la suite inverse de la suite de Syracuse. On part de $1$ et on montre qu'on atteint tout entier $n$ à une étape $m$ indice de cette suite inverse.
Mais je pense par ailleurs qu'une méthode qui permettrait de démontrer la conjecture de Syracuse serait de montrer que deux cycles de la suite ne peuvent pas être liés par un chemin. Mais alors si à partir d'un certain $n$ on n'aboutit pas à $1$, la chaîne de nombres décrite par la suite initialisée en $n$ est de cardinal infini, et ensuite par un raisonnement par l'absurde sur le cardinal de $\N$ tomber sur une contradiction. -
babsgueye a écrit:On part de 1 et on montre qu'on atteint tout entier n à une étape m indice de cette suite inverse.
Je ferai la même réponse qu'auparavant : ce serait possible uniquement si on pouvait remonter depuis 1 à l'aide d'un algorithme déterministe du type de celui de Collatz. Dans le sens ascendant, la valeur courante n'est pas complètement déterminée par la précédente, il faut faire intervenir une variable aléatoire. En d'autres termes, on ne peut inverser le $p\,\rightarrow\,n$ du sens descendant pour former $n\,\rightarrow\,p$ qu'après avoir fait le choix de $p$, tout ce dont on dispose étant $n\,\rightarrow\,(p_1,\,p_2,\,p_3,\,...)$. Le problème est d'autant plus complexe qu'on ne sait même pas de quel $p$ on a besoin à chaque étape pour atteindre l'entier $n_0$ choisi au préalable.
Comme le laissait entendre Collag3n plus haut, la nécessité de choisir est-elle la conséquence de notre ignorance ? Existe-t-il un algorithme ascendant déterministe ? -
Deux choses sont sûres : 1) le cadre probabiliste reste fumeux ; 2) il n'est rien dit du tout de la conjecture de Collatz dans ce fil.
En effet, absolument tout ce que dit Wilfrid est transposable à la situation suivante. Soit $f:\N^*\to\N^*$ l'application qui envoie $1$ sur $1$ et tout entier $n>1$ sur le quotient de $n$ par son plus petit diviseur premier. Voici les premières valeurs : \[\begin{array}{c|cccccccccc}1&2&3&4&5&6&7&8&9&10\\\hline1&1&1&2&1&3&1&4&3&5\end{array}\]Cela donne lieu à un graphe orienté dont une partie est dessinée ci-dessous (sommets : $\N^*$ ; une arête de $n$ vers $f(n)$ pour tout $n$), qui est d'ailleurs un arbre (pourquoi au fait ?). Tous les sommets sont le but d'un nombre infini de flèches (pourquoi au fait ?). On peut s'amuser à remonter les flèches « au hasard », ce qui peut donner lieu à des probabilités quand on aura précisé ce que l'on entend par là. -
Math Coss a écrit:1) le cadre probabiliste reste fumeux
A aucun moment je n'ai fait entrer le problème dans un cadre probabiliste (bien qu'un algorithme non-déterministe puisse être qualifié de probabiliste). J'ai parlé de variable aléatoire et de processus stochastique [edit], ce qui n'est pas tout à fait la même chose.Math Coss a écrit:2) il n'est rien dit du tout de la conjecture de Collatz dans ce fil.
Ce n'est pas son objet.
Ceci dit, je te remercie pour ton graphe parce qu'il est une bonne illustration du problème, mais je ne vois pas quelle eau il apporte au moulin. Ce qui serait super est que tu expliques comment remonter depuis 1 vers n'importe quel entier impair en contournant la nécessité du choix, et je ne doute pas que tu aies les compétences requises pour ce faire. -
Wilfird a écrit:pour former $n\longrightarrow$ qu'après avoir fait le choix de $p$, tout ce dont on dispose étant $n\longrightarrow (p_1 ,p_2 ,p_3 ,....)$.
Non la suite ''ascendante'' n'est pas du tout aléatoire. Quand on quitte $n$ il y a une ou deux possibilités (qui dépendent de $n$). Cette suite est la suite définie par: $a_0 = 1$ et pour $n\geq 1$
$a_n := \begin{cases} 2a_{n-1},& \textrm{ou}\\\dfrac{a_{n-1} - 1}{3},& \textrm{pour}\; a_{n-1}\,\textrm{pair et ($\equiv 1\;[3])$}.\end{cases}$
Cette évolution est complètement déterministe, même si elle ne permet pas de connaitre à partir de $n$ comment arriver à $p$, à cause des deux voies qui se présentent au niveau de certaines valeurs. -
@babsgueye,
As-tu au moins testé ton algorithme ? Les entiers à la fois pairs et $\equiv 1\;[3]$ sont 4, 10, 16, 22, 28, ...
En partant de $a_0=1$ cet algorithme produit 1, 2, 4, 1, 2, 4, 1, 2, 4, 1, ... (je manque de place pour écrire tous les termes). -
Difficile de parler de variables aléatoires et de processus stochastiques en dehors du cadre des probabilités quand même.
-
Non mon $ou$ n'est pas exclusif. De $4$ on va à $1$ et $8$, pareil pour les autres.
Mais de $2$ on ne peut aller qu'à $4$. -
@babsgueye,
Pourrais-tu couper court en donnant un exemple de suite produite selon toi par cet algorithme, parce que j'aimerais bien comprendre comment on passe de 1 à 8 ?
EDIT : finalement ne perds pas ton temps en explications, parce que si ton algorithme produit ne serait-ce qu'une seule valeur paire il cesse d'être valide, et pour une raison très simple : une suite traditionnelle de Collatz produit des valeurs paires et impaires, par exemple 7,11,17,26,13,20,10,5,8,4,2,1. Supposons que ton algorithme produise ce fameux 8, que fais-tu ensuite ? Comme la suite de 7 que tu tentes de construire n'est plus descendante mais ascendante, combien de fois vas-tu multiplier 8 par 2 avant de comprendre qu'il y a un léger souci ? Un algorithme ascendant valide ne doit produire que des entiers impairs, sinon tu peux le jeter aux oubliettes.
@Math Coss
Je n'ai pas approfondi la question, mais selon moi on parlerait de probabilités si $n$ n'avait qu'un nombre fini de successeurs $p$ (dans le sens ascendant). Disons 9. La probabilité de tomber sur la bonne valeur de $p$ à chaque étape serait de 1/9ème. Le problème est qu'une infinité de valeurs de $p$ sont associés à chaque $n$, et $1/\infty=0$. Comment parler de probabilités dans ce cas ? Merci d'éclairer ma lanterne ! -
Si on appelle $W_n$ les nombres atteints à l'étape $n$. on aura par exemple,
$W_1 = \{1\}$,
$W_2 = \{2\}$,
$W_3 = \{4\}$,
$W_4 = \{8; 1\}$,
$W_5 = \{16, 2\}$,
$W_6 = \{32, 5, 4\}$,.... ainsi de suite. (un arbre se construit à partir de $1$)
Tu vois que les $W_i$ ne sont pas forcément d'intersections vides. Mais si la conjecture est vraie, alors la réunion des $W_i$ doit recouvrir $\N$ (tous les entiers seront dans l'arbre). Cela veut dire que si tu arrives à montrer que pour un $m$ donné, il existe un $n$ tel que $m\in W_n$, ce qui n'est pas facile, alors t'auras démontré la conjecture.
Pour la suite et son inverse on ne peut pas dire l'un est aléatoire et l'autre non sinon je ne comprends pas ce que tu entends par aléatoire. -
Bien sûr que si, il y a de l'indéterminisme! La preuve, c'est que quand je multiplie 17 par 3 et que j'ajoute 1, je ne trouve pas toujours le même résultat.
-
@Wilfrid je parle comme ça, mais en mathématiques les mots scientifiques qu'on utilise sont très bien définis, pour ne pas dire avec exactitude. Un événement dont la probabilité est nulle est un événement qui ne se réalise pas. Hors ici si la conjecture est vraie (ce qui est plus plausible que le contraire) ton nombre $n$ sera surement atteint. Il n'y a rien d'aléatoire.
-
Bonjour,
> Un événement dont la probabilité est nulle est un événement qui ne se réalise pas.
Non.
Exemple: je choisis un nombre entier au hasard. La probabilité que ce soit $42$ est nulle, pourtant, c'est possible.
Cordialement,
Rescassol -
@babsgueye,
Quand je parlais d'incompréhension réciproque je faisais allusion au dialogue de sourds qui a précédé : tu me parlais de démonstration de la conjecture quand je parlais de suite inverse. Mais peu importe. Pour tenter de te faire comprendre mon point de vue, parce qu'il semble que ce ne soit pas le cas, voici un graphe inspiré de celui de Math Coss ci-dessus :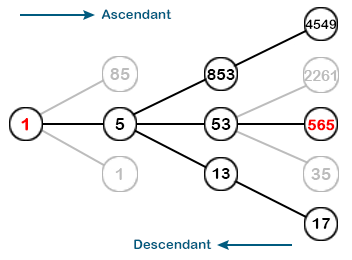
Chaque entier représenté possède une infinité de prédécesseurs (dans le sens descendant). Seuls trois d'entre eux sont représentés pour 1 (1, 5, 85), 5 (13, 53, 853) et 53 (35, 565, 2261).
Question : comment procèdes-tu pour aller de $1$ à $565$ lorsque tu ne connais pas la suite descendante $565, 53, 5, 1$ ?
@Math Coss,
Je viens de regarder la page de Wikipédia consacrée aux processus stochastiques. Il est dit : "Un processus stochastique, ou processus aléatoire (voir Calcul stochastique), ou fonction aléatoire (voir Probabilité), représente une évolution, discrète ou à temps continu, d'une variable aléatoire". Dans le cas présent la variable aléatoire est $r$, dont la valeur est fixée arbitrairement à chaque étape de la construction de la suite inverse. Elle n'évolue donc pas à proprement parler, mais il serait possible d'utiliser ce mot pour qualifier ses valeurs successives dans le contexte d'une suite inverse achevée (qui se termine par le nombre qu'on s'était préalablement fixé d'atteindre). Difficile dans ces conditions de décider si oui ou non il s'agit d'un processus stochastique.
Pour ce qui concerne le qualificatif de "suite aléatoire", une suite inverse n'est aléatoire que si on se contente d'attribuer à $r$, à chaque étape, une valeur choisie au hasard. Mais si on trouve le moyen de calculer la valeur adéquate de $r$ au lieu de laisser agir le hasard, alors la suite n'est plus aléatoire mais déterministe. -
@Wilfrid
Je reçois bien et positivement l'effort que tu fais pour se faire comprendre.
Mais en l'état des choses, le choix de $r$ à mon niveau ne peut être considéré comme aléatoire que si par exemple tu lançais une dé à une infinité de face pour le faire. C'est pas le cas. Qu'est ce qui empêche sinon de choisir un $r$ dont on connait le chemin qui y mène ? Sinon je comprendrais que tu me dises que tu choisis hasardeusement le $r$. Mais là aussi c'est que le choix du $r$ qui est aléatoire, mais pas la manière d'arriver à $r$.
Même si je comprends ce que tu veux dire, le fait de trouver dans l'espace que tu définis que la probabilité d'arriver à $r$ est nulle me gène beaucoup.
Cordialement. -
Wilfrid écrivait:
> Question : comment procèdes-tu pour aller
> de $1$ à $565$ lorsque tu ne connais
> pas la suite descendante $565, 53, 5, 1$
> ?
qui te dit qu'il n'existe pas une méthode qui permet de le trouver? Comme je te l'ai dit, le premier terme est un exposant de deux sur un exposant de trois et est très proche de $565$. Si on connaissait l'ordre de grandeur de l'erreur (toujours positive) on pourrait très bien trouver que $\frac{2^{14}}{3^3}$ est la fraction qui lui correspond. De là on connait le nombre d'étape jusqu'à 1 (c'est l'exposant de 3), après on pourrait déduire les différent $u$ sur base d'autre connaissances (e.g. le delta de la fraction inversée est <= $\frac{k}{3}$)....
bref, ce n'est pas impossible, c'est juste qu'on en connait pas assez. -
La forme du graphe autorisait la réponse "C'est facile, je vais tout droit !".babsgueye a écrit:le choix de r à mon niveau ne peut être considéré comme aléatoire que si par exemple tu lançais une dé à une infinité de face pour le faire. C'est pas le cas.
Ce n'est pas le cas, certes, mais tu peux remplacer le dé par un générateur de nombres aléatoires. Où est la différence ? Il ne va pas sortir un nombre infini, c'est vrai, mais tu auras déjà de quoi faire !Qu'est ce qui empêche sinon de choisir un r dont on connait le chemin qui y mène ?
Parce qu'on ne sait rien de $r$, raison pour laquelle on est réduits à laisser le hasard lui attribuer une valeur.le fait de trouver dans l'espace que tu définis que la probabilité d'arriver à r est nulle me gène beaucoup.
C'est ce que j'ai répondu à Math Coss à propos du cadre probabiliste dans lequel il tenait à faire entrer le problème, mais en précisant que selon moi il n'avait rien à faire avec les probabilités.
@Collag3n,
L'approximation que tu proposes de $565$ se fonde sur ta connaissance de sa suite descendante : si tu as mis $3^3$ au dénominateur c'est tout simplement parce que tu as vu sur le graphe (ou calculé) qu'elle atteignait 1 en 3 étapes. Dans ma question je précisais pourtant "lorsque tu ne connais pas" la suite descendante de $565$.
Sans cette connaissance préalable, comment t'y prends-tu pour obtenir la valeur de $x$ dans $a/3^x\approx565$ ?
Supposons néanmoins qu'après y avoir passé beaucoup de temps tu finisses par trouver la bonne approximation du terme $n$ que tu cherches à atteindre, et que tu en déduises le nombre d'étapes qui lui seront nécessaires pour atteindre 1. En quoi est-ce que ça t'aidera à calculer les termes intermédiaires de sa suite (comme 5 et 53 pour 565) ? Tu n'auras toujours aucun autre moyen que de calculer sa suite descendante !
Il n'y a pas de math (= de démonstrations) dans ce fil. Je ferme.JLT
Cette discussion a été fermée.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres





