Conjecture de Collatz éventuellement résolue?

Collag3n a écrit:

et bien qu'il soit connu que tout nombre $a\cdot 2^n-1$ monte jusqu'à $a\cdot 3^n-1$ en exactement n étapes (ni plus ni moins)

Je crains que ce ne soit pas le cas. On en a déjà discuté il y a pas mal de temps : $a\:2^n-1$ croît en fait jusqu'à $2\:a\:3^{n-1}-1$ (voir ce post).

Je vais être hors-sujet, mais pendant que j'y suis je tiens à faire remarquer que ce sont le premier et le dernier terme de ce que pour ma part je nomme une séquence croissante, lesquels sont de la forme

Premier terme : $12\:x_1-5$
Dernier terme : $12\:x_2-7$

où $x$ est un entier positif non nul et $x_1\neq x_2$. On peut calculer facilement le nombre de termes d'une séquence en fonction de la valeur de $x$ :

$12\:x-5=a\:2^n-1$
$12\:x-4=a\:2^n$
$a=2^{2-n}\:(3\:x-1)$

Prenons $x=6$. Premier terme : $12\times6-5=67$. Comme $3\times6-1=17$, impair, $n$ est nécessairement égal à 2, puisque 17 est divisible par $2^{2-2}=1$. Et de fait, la suite de 67 est 67, 101, 19, ..., soit deux termes croissants. Avec $x=7$ on a $12\times7-5=79$ ; comme $3\times7-1=20$, divisible par 4, l'exposant de 2 doit être égal à $-2$, soit $n=4$. Suite de 79 : 79, 119, 179, 269, 101, ... Il y a bien 4 termes croissants. On notera que ni 67 ni 79 n'ont de prédécesseur plus petit qu'eux, condition pour qu'ils soient le premier terme de leur séquence croissante respective.

On opère de la même façon pour le dernier terme de la séquence :

$12\:x-7=2\:a\:3^{n-1}-1$
$12\:x-6=2\:a\:3^{n-1}$
$a=3^{2-n}\:(2\:x-1)$
$x=\displaystyle\frac{1}{18} \left(a\:3^n+9\right)$

$a$ étant un entier impair on peut lui attribuer n'importe quelle valeur pour obtenir celle de $x$, qu'on remplacera dans $12\:x-7$. Supposons qu'on désire obtenir le dernier terme d'une séquence croissante de 5 termes. Avec $a=1$ et $n=5$ on obtient $x=14$ puis $161$, dernier terme de la séquence croissante 31, 47, 71, 107, 161, ... Avec $a=3$ et $n=11$ on obtiendra $354293$ et la séquence de 11 termes croissants 6143, 9215, 13823, 20735, 31103, 46655, 69983, 104975, 157463, 236195, 354293, ...

Collag3n a écrit:

il n'est par contre pas connu si après ces n étapes, et une division par 2 supplémentaire, on ne retombe pas sur un autre $a\cdot 2^n-1$ qui remontera de plus belle.

Une suite de Collatz est constituée de séquences croissantes liées entre elles, ce qui lui donne cet aspect caractéristique de montagnes russes. Le vrai problème n'est pas de savoir si lorsque l'une d'elles se termine on ne vas pas retomber sur une autre, mais de comprendre pourquoi l'une d'elles est la dernière.

@LEG,

Je ne voulais pas trop interférer avec le sujet initial, mais comme il semble éteint je me permets de poursuivre.

Wilfrid a écrit:

Le vrai problème n'est pas de savoir si lorsque l'une d'elles se termine on ne vas pas retomber sur une autre, mais de comprendre pourquoi l'une d'elles est la dernière.

LEG a écrit:

Parce que la conjecture est vraie pour l'instant...

C'est en effet d'une logique implacable, mais ne constitue pas une explication. Voici un schéma illustrant ce dont je parlais :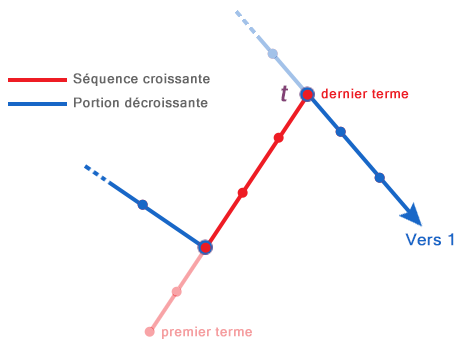


S'il existe des séquences croissantes aussi longues qu'on veut et dont les premier et dernier terme sont calculables, il n'existe par contre aucune séquence décroissante, mais plutôt des "portions décroissantes de la suite" dépourvues de premier terme (au sens qu'il serait uniquement précédé d'un terme plus petit que lui, ce qui permettrait de l'identifier formellement, tout comme le premier terme d'une séquence croissante est uniquement précédé d'un terme plus grand que lui – ou n'a aucun prédécesseur s'il est un multiple de 3). On sait seulement qu'une telle portion débute par le dernier terme d'une séquence croissante et vient se greffer sur l'un des termes de la séquence croissante suivante, ou, si celle-ci n'existe pas, s'achève sur 1.

Le terme $t$, appartenant à la dernière séquence croissante, est à mon sens le terme le plus important d'une suite. Une infinité de chemins mènent à lui, si bien que tout ce qui le précède peut être considéré comme superflu.

La question est donc : le terme $t$ est-il particulier ? La difficulté réside dans le fait que chaque terme de la dernière portion décroissante peut être considéré comme un terme $t$ à condition qu'il soit également le dernier terme potentiel d'une séquence croissante, donc de la forme $12\:x-7$. Si aucun terme d'aucune dernière portion décroissante n'est de cette forme (hormis bien sûr le premier), alors $t$ est particulier.

NB : parmi les prédécesseurs impairs immédiats de 1 certains sont de cette forme : 5, 341, 21845, ...