Conjecture de Syracuse
Réponses
-
Bonjour
je ne savais pas que ma démo. sur Syracuse (12/2015) a été citée dans la récap de L.O. Pochon et Alain FABRE - page 38-39 ( 2017)
où ils faisaient des remarques relatives à la page 12 de mon papier alors que ce dernier ne comportait que 11 ??
Ils ont aussi signalé le lien de mon doc en référence pour ceux ou celles intéressés par Syracuse.
@Dom : ma démo est aussi terrible que mon dernier message.
b.rgds
BERKOUK -
Le discours habituel : « je ne sais pas faire ce que tu demandes mais on a parlé de moi en bien. »
Je réitère mes trois suggestions.
Voir message précédent. -
BERKOUK3 a écrit:vérifier le point 1° [il n'existe qu'un seul cycle trivial] c'est comme si on démontre qu'il existe un et un seul endroit sur le globe terrestre de coordonnés " 4-2-1" ou tous les avions une fois arrivés à cet endroit , commencent infiniment à tourner en rond
Il existe une explication beaucoup plus simple à l'existence du cycle trivial : dans une suite composée uniquement de ses termes impairs, chacun d'eux est calculé par l'algorithme condensé
$n_{i+1}=\dfrac{3\;n_i+1}{2^k}\to n_i=\dfrac{n_{i+1}\;2^k-1}{3}$
Or, parmi tous les entiers impairs $n$, un seul est à la fois son propre prédécesseur et son propre successeur : 1. Il est le seul à pouvoir remplacer simultanément $n_i$ et $n_{i+1}$. Tout autre entier impair possède un prédécesseur et un successeur différents de lui et ne peut donc pas former un cycle. Lorsque la suite tombe sur 1 elle est en quelque sorte piégée, ce qui est la conséquence de la formulation du problème $3\;n+1$ et n'a rien à voir avec la conjecture selon laquelle toute suite se termine par 1.
Donc exit le cycle trivial. -
[suite du précédent]
D'ailleurs si on pose
$n_2=\dfrac{3\;n_1+1}{p}$ et $n_1=\dfrac{n_2\;p-1}{3}$
et qu'on se demande dans quelles conditions $n_1=n_2$, on trouve
$p=\dfrac{3\;n_1+1}{n_1}$
On sait que $p$ est pair puisque c'est une puissance de 2 :
$n_1$ pair : $3\;n_1+1$ impair $\to$ impossible.
$n_1$ impair : $3\;n_1+1$ pair $\to$ $p$ pair.
$n_1$ doit donc être impair et le quotient égal à 2, 4, 8, 16, ... Quelles valeurs de $n_1$ satisfont à ces conditions hormis $n_1=1$ ? -
Ici, tu analyses les cycles constitués avec 3 nombres : résoudre l'équation x=(3x+1)/4
Mais ceci ne prouve pas qu'il n'y a pas de cycle de n nombres, avec n>3.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Je préfère en rester aux suites composées de termes impairs uniquement, plus simples à gérer. Ce dont j'ai parlé ci-dessus équivaut donc au cycle de longueur 1 $n_1, n_1, n_1, ...$, et en l'occurrence 1, 1, 1, 1, ...
Soupçonner l'existence de cycles de longueur supérieure à 1 est contraire à l'idée qu'on se fait d'un arbre des suites dans lequel chaque terme impair est unique. Le terme impair $n$ possédant une infinité de prédécesseurs calculables, il existe une infinité de chemins menant à lui, mais il n'en demeure pas moins unique. Il possède un successeur unique, qui lui-même possède un successeur unique, etc., parce que l'algorithme de Collatz n'admet qu'une seule solution à chaque étape.
Prenons l'extrait d'une suite $..., n_1, n_2, ..., n_L, n_1, ...$ dans lequel on observerait la formation du cycle de longueur $\small{L}\:$$n_1, ..., n_L$. La figure suivante, dans laquelle $p_r$ est le prédécesseur de $n_1$ de rang $r$, montre ce qui se passerait :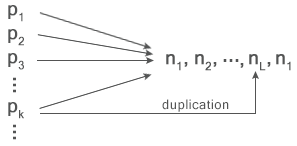
On pourrait penser qu'avec le cycle $\color{red}{p_1}, n_1, n_2, ..., \color{red}{p_3}, n_1$ il n'y aurait pas de duplication de terme, mais le problème vient du fait que la suite dans laquelle il serait supposé figurer appartient à l'arbre des suites, et que le second $p$ étant toujours dupliqué, l'arbre contiendrait deux fois le même terme impair, ce qui par définition est impossible. Par conséquent il ne peut pas exister de cycle de longueur > 2, parce que $p, n, p, n, ...$ pourrait éventuellement exister (pas de duplication). Il faudra approfondir la question. -
J'ai réécrit le dernier paragraphe de mon précédent message pour le clarifier.
-
Et pourquoi pas plutôt supprimer purement et simplement ce message qui ne voulait rien dire ?Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin
-
Si sa compréhension te pose problème, fais-le moi savoir !
-
Wilfrid, tu ne serais pas le premier à nous dire qu'on a des problèmes de compréhension, ou que "1+1 font 2, ce que les experts ne savaient pas à l'époque" (message que tu as modifié entre-temps, mais qui ressemble furieusement au message de lionel).
Quoique, il y a quand-même quelque chose que je ne comprends pas: comment peux-tu parler de "un cycle est impossible....c'est absurde...c'est tellement évident" alors que tu as aussi travaillé sur 5n+1 ? -
Wilfrid : dans ce message ICI, tu fais de la prose mais tu ne prouves rien. Tu affirmes des choses, et il n’y a pas d’argumentation.
Je précise
Tu dis : « Il existe une explication beaucoup plus simple à l'existence du cycle trivial »
Tu annonces donc la couleur : tu veux expliquer et non pas démontrer.
a) « dans une suite composée uniquement de ses termes impairs, chacun d'eux est calculé par l'algorithme condensé »
Mouais. Déjà des symboles, rien de quantifié.
b) « Or, parmi tous les entiers impairs n, un seul est à la fois son propre prédécesseur et son propre successeur : 1»
Une affirmation, bon...
c) « Il est le seul à pouvoir remplacer simultanément ni et ni+1»
Une affirmation, bon, bon...
d) « Tout autre entier impair possède un prédécesseur et un successeur différents de lui et ne peut donc pas former un cycle ». Une affirmation, avec un « DONC » dont on ne sait d’où il vient.
e) « Lorsque la suite tombe sur 1 elle est en quelque sorte piégée »
Une affirmation. C’est la seule que je comprends sans réfléchir mais c’est encore une affirmation.
f) « Donc exit le cycle trivial »
Une affirmation. Un « DONC ».
Comprends-tu que la discussion n’existe pas ?
NB : je ne dis pas que ces choses sont fausses. Je dis qu’il s’agit d’un discours avec des affirmations.
Mais je dis qu’on ne voit pas du tout de maths là dedans.
Ça fait penser à un invité qui a 30 secondes pour s’exprimer sur la preuve de cette conjecture sur une chaîne d’info.
C’est juste impossible.
Mais ici, tu as le temps, tout le temps que tu veux.
Donc rédige des maths, directement sur ce forum, sans te contenter seulement de citer des liens, des documents et que sais-je encore.
Une preuve, une vraie, est faite pour convaincre tout le monde.
Respecte ces codes, respecte les codes d’une démonstration. Tu devrais alors être pris au sérieux. Et aussi, les réponses, même si elles disent que tu as tort seront « propres » et t’aideront à voir si ton raisonnement contient des failles.
Tout le blabla, ça ne sert à rien. -
Bon, il est possible que mes explications n'étaient pas suffisamment claires. Je reprends, en commençant par insister sur le fait qu'ici il n'est question que de suites de Collatz constituées de leurs seuls termes impairs.
Prenons deux termes consécutifs $p$ et $n$. Sachant que $p$ est le prédécesseur de $n$, lorsqu'on cherche à calculer $n=(3\;p+1)/2^u$ ou $p=(2^u\;n-1)/3$ on se heurte toujours à l'inconnue qu'est $u$. Mais lorsqu'on pose
$p_r=\dfrac{2^{2\,r-(m-1)}\;n-1}{3}$, avec $r$ entier naturel > 0 et $m=n\;\text{mod}\;3$,
on peut calculer tous les prédécesseurs de $n$. Par exemple, quels sont les 5 premiers prédécesseurs de 23 ? $m=$ 2 et $r=$ successivement 1, 2, 3, 4, 5, ce qui donne $p=$ 15, 61, 245, 981, 3925. Un prédécesseur sur 3 est un multiple de 3, mais dans ce qui suit on admettra qu'ils ont été éliminés.
Passons maintenant au cycle $n_1, n_2, ..., n_L, n_1, n_2, ..., n_L, n_1,$ etc., donc de longueur $\small{L}$, que je fais maintenant débuter par le prédécesseur de $n_1$ : $p_x, n_1, n_2, ...$ et ensuite ? $n_L$ étant le prédécesseur de $n_1$, il appartient nécessairement à l'ensemble des prédécesseurs de celui-ci, et le cycle s'écrit $\color{gray}{p_x,} n_1, n_2, ..., p_y$. La suite complète, terminée par $p_y$, peut-elle figurer dans l'arbre des suites ? Bien sûr que non puisque $p_y$ y figure déjà, et que par définition aucun entier impair ne peut se trouver en double exemplaire dans cet arbre ! Si cette suite ne peut pas figurer dans l'arbre elle n'existe tout simplement pas.
Si on commençait à admettre la duplication de termes impairs il faudrait ensuite se demander combien d'exemplaires peuvent se trouver dans l'arbre. Mais non, cette question serait inutile puisque l'arbre aurait cessé d'exister !
Reste le cas du cycle de longueur 2 $p, n, p, n, ...$, qui ne souffre d'aucune duplication et pourrait de ce fait exister. Mais comme je l'ai dit plus haut, il faudrait que $p$ soit à la fois le prédécesseur et le successeur de $n$, ce qui n'est possible que lorsque $p=n=1$.
Conclusion : il n'existe aucun autre cycle que 1, 1, 1, ... -
Tu n’as pas dû lire mon message (on a dû se croiser).
Je m’intéresse à une nouvelle affirmation : « on peut calculer tous les prédécesseurs de n ».
Prenons n=1. Quels sont tous ses prédécesseurs ? Peux-tu les « calculer » ? -
"par définition aucun entier impair ne peut se trouver en double exemplaire dans cet arbre ! Si cette suite ne peut pas figurer dans l'arbre elle n'existe tout simplement pas."
Par quelle définition? Sinon, la racine de ton arbre c'est quoi d'après toi ? C'est pas un "cycle" ?
La forêt dans 5n+1, tu l'as explorée ou pas? -
1 mod 3 = 1, $2^{2\,r-(1-1)}=2^{2\,r}$. En donnant à $r$ les valeurs successives 1, 2, 3, ..., $\infty$ on obtient les prédécesseurs de 1 que sont 1, 5, 85, 341, 5461, 21845, ..., $\infty$.
-
Si on s'intéressait pour une fois à quelqu'un qui va « un peu plus près de Syracuse » ? (Oui, cela a un air de déjà vu.)
-
Corrige moi si je me trompe.
Tu dis que dans un arbre, tous les chemins mènent au tronc, ou à la racine. Comme on a un arbre, il n'y a donc pas de cycle.
C'est bien ça que tu dis ?
En soi, le raisonnement est exact.
Mais le but de l'exercice, c'est justement de démontrer que tous les chemins mènent à 1. ou de montrer que c'est un 'arbre'. Donc on ne peut pas utiliser cette information. Elle n'est pas acquise, puisqu'on cherche à la démontrer.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
@lourran,
Je souscris à ton argument selon lequel il n'a jamais été démontré que 1 se trouvait à la racine de l'arbre, malgré les très fortes présomptions qui pèsent en sa faveur. Le problème n'est cependant pas là.
On peut se représenter l'ensemble des prédécesseurs $p_r$ de $n_1$ comme une bande verticale. Construire une suite de Collatz revient ni plus ni moins à passer d'une bande à l'autre. La position verticale de la trajectoire lors de son passage sur une bande n'a aucune influence sur la position qui sera la sienne à son arrivée sur la bande suivante, puisque l'algorithme de Collatz n'admet qu'un seul successeur. L'indéterminisme fait son apparition lorsqu'il s'agit de construire une suite à l'envers : à chaque étape on doit choisir au hasard la position verticale de la trajectoire sur la bande précédente.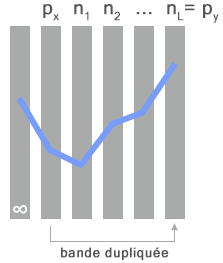
Le prédécesseur du premier terme d'un cycle appartient nécessairement à la même bande que son dernier terme. La seconde bande est une chimère, il est en réalité impossible qu'elle soit là, et ceci reste valable quelle que soit la racine de l'arbre. -
Encore un discours.
Très beau, mais non mathématique.
Bye bye. -
Regarde 5n+1 et tu comprendras ce qui se trouve à la racine d'un (des) arbre(s). Et la tout ton discours n'apparaîtra que comme du vent.
-
Illustration du concept de "bandes verticales" évoqué dans mon précédent message :
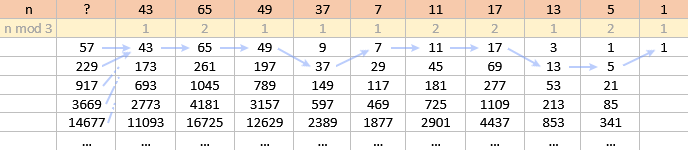
Le prédécesseur de 43 étant indéfini, on peut faire débuter la suite par n'importe lequel d'entre eux. Ensuite il n'existe plus qu'un seul chemin vers 1. Si on avait voulu que la suite passe par 173 (second terme de la colonne 43) on aurait eu le choix entre la faire débuter par ce nombre ou remplacer la suite de prédécesseurs de la première colonne par 115, 461, 1845, 7381, ..., prédécesseurs de 173. Mais le reste de la suite, à partir de 65, qui est le successeur de 43 aussi bien que de 173, n'aurait pas changé. Si on remplaçait 43 par un terme n'appartenant pas à sa colonne, la suite obtenue serait différente en partie ou en totalité (bien que les deux derniers termes seraient probablement identiques).
Si au lieu de nommer les en-têtes de colonnes par la suite de 43 on les nommait par la suite des entiers impairs, la progression de la suite de Collatz obtenue ne serait plus uni mais bidirectionnelle (il s'agit ici de la suite de 25) :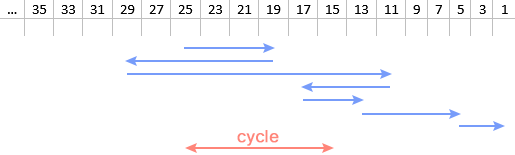
Cette manière de représenter une suite de Collatz permet de se faire une meilleure idée de la notion de cycle : qu'importe sa longueur, ses premier et dernier termes renvoient l'un à l'autre. Dans mes exemples précédents il s'agissait de $n_1$ renvoyant à $n_L$ en $\small{L}$ étapes, qui renvoyait à $n_1$ en une seule étape, exploit illustré par l'extrait suivant du graphe d'une suite :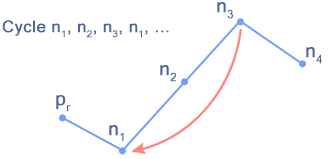
Au lieu de poursuivre vers $n_4$ comme on s'y attendrait, $n_3$ retourne à $n_1$ alors que le prédécesseur de celui-ci est $p_r$ et non $n_3$.
Bon, je me suis quelque peu répété, mais mon objectif était d'en finir une bonne fois pour toutes avec l'arbre des suites de Collatz, que j'avais eu la mauvaise idée de mettre à contribution et qui compliquait inutilement les choses.
Si quelqu'un n'est toujours pas convaincu de l'impossible existence d'un cycle autre que 1, 1, 1, ..., qu'il veuille bien m'expliquer ce qui pourrait la rendre possible. -
Mode fantôme \on :
Les maths ce n’est pas d’être convaincu mais de convaincre tout le monde.
Pour convaincre, il faut des preuves mathématiques.
Mode fantôme \off. -
Bonsoir,
Dom, (tu)
Cordialement,
Rescassol -
De belles "bandes verticales" en 5n+1....oh, mais que vois-je? IMPOSSIBLE!!!
-
Tu nous dis quoi : Tu nous dis que sur tous les essais que tu as faits, tu n'as jamais constaté de cycle, et tu as constaté que tous les chemins mènent au nombre 1.
Et donc comme tous les nombres testés n'ont jamais généré de cycle autre que le cycle (1,4,2) , tu dis que c'est certain, il ne peut pas y avoir de cycle autre que (1,4,2).
Tu as très probablement raison, il n'y a probablement pas d'autre cycle que le cycle (1,4,2).
Mais tout ce que tu dis là , c'est exactement ce qu'a dit Collatz il y a près d'un siècle.
Il a dit : "j'ai testé plein de nombres entiers, j'ai fait tels calculs, et à chaque fois j'arrive au cycle (1,4,2). Je pense que cette propriété est vraie pour tous les entiers, j'en ai l'intime conviction, mais malheureusement, malgré des années de recherche, je n'arrive pas à démontrer que cette propriété est vraie pour tout entier. "
Et toi, tu dis la même chose ... tu recopies ce qu'il a écrit à l'époque. Le problème, c'est que tu ne recopies pas mot-pour-mot ce qu'il a écrit ; tu n'as pas plus d'élément que lui, tu as exactement les mêmes résultats que lui, voire moins que lui. Mais lui, à partir de tous ces éléments, il concluait : Je pense que bla bla. Et toi, avec les mêmes éléments, voire moins, tu conclues : j'ai la preuve que bla bla.
Pour rappel, voici la définition du mot Conjecture : Opinion fondée sur des suppositions, des probabilités.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Je pensais qu'après trois approches différentes j'aurais réussi à me faire comprendre, mais je constate que malheureusement ce n'est pas le cas. Si je trouve une quatrième manière d'expliquer tout ceci je ne manquerai pas de la poster !
-
Même convaincre n'a que peu d'intérêt. S'il m'arrive encore d'explorer des pistes sur cette conjecture, ce n'est pas pour être convaincu (1 seule fois dans le tableau).
-
Bonjour
Je crois que si on vérifie indépendamment les trois étapes suivantes, on pouvait, dans ce cas, approcher la conjecture à savoir :
1)- il existe un et un seul cycle dans la suite de Collatz, c’est le cycle trivial 4-2-1 ;
2)- quelque soit un entier n ... la suite de Collatz décroît vers un n’ tel que n’ soit strictement inférieur à n ;
3)- quelque soit un entier ... la suite de Collatz, atterrit dans le cycle trivial dont 1, est le plus petit élément.
"le meilleur moyen de résoudre un problème, c'est de le couper anatomiquement en divers parties, au lieu de le complexifer "
elle est prête.
BERKOUK -
Flûte, ça recommence :
Le 2) est faux. Choisir $n=1$ et trouver $n’$.
Le 3) est la conjecture de Collatz.
Seul le $1)$ est intéressant.
Le $2)$ est aussi intéressant mais est mal rédigé. -
Formulation correcte du 2) : pour tout entier n supérieur ou égal à 2, il existe des entiers p et n', avec n'<n, tels que u(p)=n', où u est la suite de Syracuse ISSUE DE n.
Mais ça fait pas loin de 90 ans qu'on sait ça, alors le schilimimi n'avance pas beaucoup... -
BonjourBerkouk a écrit:2)- quelque soit un entier n ... la suite de Collatz décroît vers un n’ tel que n’ soit strictement inférieur à n ;
-completez les points de suspension ...
-d'accord Monsieur...
"2)- quelque soit un entier n > 1 la suite de Collatz..."
- ça commence bien , avant meme de consulter le papier
BERKOUK -
Orienté vers cette conversation ancienne lors d'une recherche Google, j'ai été sidéré par cette longue série de messages pas toujours très "élégants" et parfois empreints de psychorigidité. Mais ce qui est le plus atterrant, c'est qu'une démonstration qui contient une grossière erreur de logique ait pu être publiée par un matheux au CV impressionnant, validée selon ses dires par plusieurs experts puis revalidée par un comité de lecture HAL. Soit les experts ne savent pas lire, soit le niveau technique est devenu calamiteux. A ce jour, cette démonstration figure toujours aux archives HAL alors qu'elle devrait être retirée.
Inutile de dégainer son pedigree ou d'en venir à des attaques personnelles comme c'est la mode maintenant, mais de mon temps, un élève ordinaire en classe de 6ème aurait été capable de démontrer que même si la suite de Collatz de 8m+3 contient effectivement un proche successeur de la forme 4p+1 (p = 3m+1), malheureusement il ne pourra pas démontrer que le successeur de 4p+1 qui sera effectivement inférieur à 4p+1, sera aussi inférieur à 8m+3 le nombre de départ ! Notre jeune élève de 12 ans montrera même que ce successeur aura exactement pour valeur 9m+4, compris entre 8m+3 et 4p+1. Et l'élève ne pourra aller plus loin sans préjuger de la parité de m. Il montrera plus tard que cette piste de décomposition en 2 sous-ensembles est sans issue. Elle ne présente un intérêt que pour réduire le nombre de cas à traiter par calculs informatiques. -
Les archives HAL ne sont pas à comité de lecture, il s'agit d'un site de dépôt de prépublications.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres









