Écart max
Réponses
-
Un cardinal est un nombre. Un nombre (entier positif ou nul) est un cardinal. Le cardinal d'un ensemble, c'est le nombre d'éléments de cet ensemble.
Dans les exercices simples de dénombrements, on a souvent des question où le cardinal est la multiplication d'autres cardinaux.
Mais ce n'est pas systématique, loin de là.
Par exemple : Je lance 3 pièces (1 bleue, 1 blanche et 1 rouge) à pile ou face, quel est le nombre de cas possibles (=8) . Quel est le nombre de cas possibles où toutes les pièces tombent sur pile (=1) , Quel est le nombre de cas possibles où au moins une pièce tombe sur face (=8-1=7).
Cardinal du dernier ensemble = 7.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Cest vrai que j'avais oublié que les cardinaux sont sujets à beaucoup de manipulations : CardA + Card B. Card B-Card A etc...
-
Bonjour,jeancreatif a écrit:Bonsoir Alea, tu m'as convaincu de me mettre à la programmation.
Que choisir de moins "prise de tête" ? Python ou ton Julia ?
Je te conseille le langage Wolfram (Mathematica), puissant, rapide, très compact et plus simple à comprendre que nombre d'autres langages (mais tout est relatif).
Si j'ai bien compris, on effectue 20 lancés d'une pièce de monnaie et on compte le nombre de "pile" consécutifs obtenus, qui peut se situer entre 1 et 20. On répète cette série de lancés un grand nombre de fois. Le résultat final est une liste de 20 nombres représentant le nombre total de fois qu'on a obtenu 1, 2, 3, ..., 20 "pile" consécutifs.
Ça revient à effectuer 20 tirages pseudo-aléatoires de 0 et de 1, en admettant que 0 = pile. Donc pour commencer je crée un liste de 20 zéros :
res=ConstantArray[0, 20]
dont j'incrémenterai chaque terme au fur et à mesure des résultats, sachant que le premier 0 est à l'indice 1 de cette liste. Par exemple, si après 20 lancés j'ai obtenu 3 zéros consécutifs, je ferai res3++. Pour simuler les 20 tirages je crée ensuite une liste de vingt 0 et 1 tirés aléatoirement :
RandomInteger[1, 20]
RandomInteger[k, 20] produit un entier pseudo-aléatoire de 0 à k. Supposons que cette liste soit {0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0}, dont le plus grand nombre de zéros consécutifs est 4. Pour obtenir ce nombre je pose
r=Max@SequenceCases[{0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0}, {p:Repeated[0]}:>Length[{p}]]
SequenceCases[...] renvoie {1, 3, 4, 2, 1}, qui correspond aux nombres de 0 consécutifs rencontrés dans cette liste, et dont Max prélève la valeur maximale, soit r = 4. Il ne reste plus qu'à incrémenter l'indice correspondant de la liste res : res4++. Voici la fonction consec0 (0 consécutifs) où nbrSer est le nombre de séries de "lancés de la pièce", et lanc le nombre de lancés effectués au cours de chaque série (20 par défaut) :
Résultats de consec0[10^6, 50] : {27, 17226, 155830, 275549, 237068, 148912, 81760, 42168, 21112, 10368, 5039, 2491, 1206, 634, 320, 147, 67, 35, 24, 7, 5, 4, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Graphe des 24 premiers totaux (jusqu'au 1) :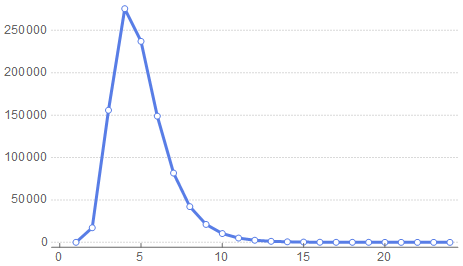
Je suppose qu'on pourrait augmenter le nombre de séries de lancer sans voir la forme du graphe changer.
Une variante, beaucoup plus rapide (20 s contre 30 mn pour 10^6 séries de lancés), consiste à prendre en compte pour chaque série la séquence de chiffres identiques la plus longue, qu'elle soit composée de 0 ou de 1 :
Je reprends l'exemple de RandomInteger[1, 20] = {0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0} :
Split[{0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0}] = {{0}, {1, 1, 1}, {0, 0, 0}, {1, 1}, {0, 0, 0, 0}, {1, 1}, {0, 0}, {1, 1}, {0}}
Length /@ Split[{0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0}] = {1, 3, 3, 2, 4, 2, 2, 2, 1}, la longueur de chaque sous-liste. Puis Max[...] renvoie bien sûr 4, qu'il s'agisse d'une séquence de 0 ou de 1. Vu la rapidité de ce nouvel algorithme j'ai testé
consec01[10^8, 50] = {0, 3688, 1872734, 16032503, 27684193, 23519355, 14691106, 8021712, 4124500, 2058518, 1017753, 498277, 243790, 118477, 58254, 28382, 13795, 6576, 3298, 1610, 752, 373, 192, 82, 47, 22, 7, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Alors que précédemment la plus longue séquence de chiffres identiques était majoritairement de longueur 4, cette fois-ci elle est de longueur 5, mais le graphe a exactement la même forme (29 premiers totaux, jusqu'au 1) :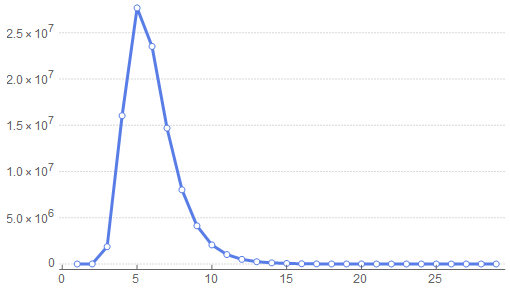
On notera que sur 50 "lancés" il y a toujours au moins deux 0 ou deux 1 consécutifs, puisqu'il n'existe aucune séquence de longueur 1.
Bref, rien de nouveau, c'était juste pour montrer la simplicité du langage Wolfram par rapport à Python, Julia et autres joyeusetés.
EDIT : tout bien réfléchi, je pense que le décalage de la longueur majoritaire d'une séquence de chiffres identiques, de 4 dans le premier exemple à 5 dans le second, est dû au fait que j'ai effectué 10^6 séries de 50 "lancés" dans le premier cas, contre 10^8 dans le second. Vu qu'il a fallu 30 mn pour obtenir le premier résultat, si je passais de 10^6 à 10^8 il faudrait 100 fois plus de temps, soit 50 heures. Je ne vais donc pas m'amuser à vérifier mes soupçons. Quoi qu'il en soit, il se pourrait que prendre en compte uniquement les 0 et prendre en compte les 0 et les 1 indifféremment, revienne exactement au même. Ce qui compte en effet c'est la plus longue séquence de chiffres identiques obtenue, et elle ne varie pas avec la nature desdits chiffres puisqu'en comptant les "pile" on obtient la même chose qu'en comptant les "face". -
Merci beaucoup Wilfrid pour ta contribution. Nous disposons maintenant de bien des résultats et de méthodes intéressantes.
-
Si on passe de 4 à 5 entre les 2 courbes, ce n'est absolument pas parce que le nombre d'expériences passent de 10^6 à 10^8, mais parce qu'on passe de 20 à 50.
Refais les 2 expériences suivantes : calculer consec01[10^8, 20] et consec01[10^6, 50], tu verras que le nombre d'expériences n'a pas d'impact sur la forme de la courbe ni sur la valeur x qui donne le point maximal.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
@lourran,
Tu as mal lu, dans les deux cas j'ai utilisé des séries de 50 "lancés".
Mais tu as raison sur le second point : si on exécute consec01[10^n, 50] avec n successivement égal à 3, 4 ,5, 6, 7, 8, dans tous les cas la séquence majoritaire est de longueur 5. La question se pose donc de savoir pourquoi elle est de 4 lorsqu'on ne tient compte que des 0, et je ne pense pas qu'en répétant l'expérience 10^8 au lieu de 10^6 fois changerait quoi que ce soit. En effet, en posant A = consec0[10^6, 50] et B = consec0[10^8, 50], si la séquence majoritaire de 0 dans A est de longueur 4, calculer B conduirait au même résultat que calculer 100 fois A : on obtiendrait 100 fois une séquence majoritaire de longueur 4. J'en déduis que quelle que soit la valeur de n, la longueur de la séquence majoritaire dans consec0[10^n, 50] ne peut être que 4, tout comme elle est de 5 dans consec01[10^n, 50]. -
@Wilfrid : c'est sans doute une question d'habitude / goût mais je trouve le code Julia nettement plus clair que le code Mathematica.
Par ailleurs, sauf erreur, Wolfram est payant... contrairement à python ou Julia.
Sinon jean je t'invite à plutôt comprendre la démarche de Lucas pour le calcul exact de la loi du nombre max de 1 successif. -
Bonjour,
Sylviel, Python, pas python :-D
Cordialement,
Rescassol -
Sylviel a écrit:Sinon jean je t'invite à plutôt comprendre la démarche de Lucas pour le calcul exact de la loi du nombre max de 1 successif.
Sylviel, je suis très reconnaissant envers Lucas, qui est le seul à nous avoir donné une matrice disposant d'une relation de récurrence explicite (on passe de la matrice de transition directement à n =10000 si on le souhaite). Egalement un coup de chapeau à Lou16, qui, comme par magie, a donné une formule, qui est celle que je cherchais.(Cependant, l'un comme l'autre , pour avoir p(xn)=k, passent par p >= K, (chez Lou16, p<=k).
En revanche, je ne comprends pas l'interêt de Lucas pour Log base 2.... Car cela ne désigne ni la suite max de "pile", ni même la proba maximum à partir de ce point. Un exemple, pour n=20, la proba maximum est égale à 3 "pile" et non pas à 4 "pile" qui correspond au Log base 2. (Si j'ai raté un truc, je serais content de l'apprendre). -
Sylviel a écrit:@Wilfrid : c'est sans doute une question d'habitude / goût mais je trouve le code Julia nettement plus clair que le code Mathematica.
Quelqu'un aurait-il la bonté de m'expliquer pourquoi les séquences de 4 chiffres identiques sont les plus fréquentes lorsqu'on ne prend en compte que les 0, et qu'elles sont de 5 chiffres lorsqu'on ne différencie pas les 0 et les 1, ce qui paraît totalement contrintuitif ?
En attendant, et bien que ce soit hors sujet, il me semble important que ceux qui envisagent de se mettre à la programmation fassent la différence entre un langage procédural (Wolfram) et un langage séquentiel (les autres). Il ne faut pas voir le langage Wolfram comme un langage de programmation au sens habituel du terme, mais comme une boîte de Lego. C'est un vaste ensemble de procédures (routines, fonctions) dont on combine un certain nombre pour obtenir le résultat recherché. Un programme en langage Wolfram est plus simple à mettre en œuvre qu'un programme séquentiel ordinaire puisqu'on ne se préoccupe pas de savoir comment parvenir à tel ou tel résultat intermédiaire : on se focalise uniquement sur l'objectif à atteindre, tout comme comme on le fait pour construire un objet quelconque à l'aide des briques d'une boîte de Lego. Il faut juste se familiariser avec quelques subtilités syntaxiques (comme la séquence "/@" rencontrée ci-dessus).
Pourquoi réinventer la roue à chaque fois qu'on se lance dans l'écriture d'un programme ? Telle est la philosophie de nombre de programmeurs, qui se constituent au fil du temps une bibliothèque de routines spécifiques à leurs besoins, qu'il réutilisent encore et encore. Chez Wolfram Research il y a des gens hautement qualifiés qui ont déjà constitué cette bibliothèque, destinée aux scientifiques et en particulier, bien évidemment, aux mathématiciens.
Voici un exemple particulièrement significatif. Je reprends la liste {0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0} qu'il faut séparer en morceaux composés de chiffres identiques pour ensuite déterminer lequel est le plus long (sans différenciation des séquences de 0 et de 1). Pour ça j'utiliserai le langage de script PHP, parce qu'il se lit facilement.
[size=large]PHP[/size]<?php $arr = [0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0]; // conversion du tableau (array) en chaine de caractères $chn = implode("", $arr); // on n'insère rien entre les caractères $lg = strlen($chn)-1; // longueur de la chaine - 1 // on parcourt la chaine pour détecter tout changement de caractère (chiffre) $i = 0; while ($i < $lg) { if ($chn[$i+1] != $chn[$i]) { // le caractère à la position $i+1 est différent de celui à la position $i // on insère un espace entre les deux, donc à la position $i+1 $chn = substr_replace($chn, " ", $i+1, 0); // 0 signifie insertion (pas remplacement) // on incrémente le pointeur pour le placer sur l'espace // et on n'oublie pas d'incrémenter la longueur de la chaine $i++; $lg++ } $i++ } // création d'un tableau contenant les morceaux séparés par un espace $res = explode(" ", $chn); $lg = count($res); // nombre d'éléments du tableau $plsq = 0; // plus longue séquence de chiffres identiques for ($i=0; $i < $lg; $i++) { $k = strlen($res[$i]); // longueur du morceau if ($k > $plsq) $plsq = $k } // afficher le résultat echo $plsq ?>Avec du temps devant soi on pourrait trouver d'autres manières de procéder, qu'elles soient plus simples ou plus compliquées.
[size=large]Mathematica[/size]plsq = Max[Length /@ Split[{0,1,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0}]]Pour les explications voir mon second précédent message.
Pourquoi s'emmerder à concevoir un algorithme et taper 28 lignes de code que quelqu'un devra lire jusqu'au bout pour comprendre son fonctionnement – et éventuellement chercher à faire mieux –, alors qu'on peut se contenter d'une seule ligne déjà dans sa forme la plus aboutie et dont la finalité apparaît immédiatement pour peu qu'on ait quelques bases en langage Wolfram ?
Il est évident qu'en interne Mathematica se livre à un tas de calculs peut-être semblables à ceux que j'ai codés en PHP, mais c'est le cadet de nos soucis ! Je suppose par ailleurs qu'il met à profit le mécanisme de type Lego que ses concepteurs ont créé, afin d'éviter toute duplication de code. C'est probablement ce qu'entend Stephen Wolfram lorsqu'il dit que Mathematica est complètement optimisé.
Je précise pour terminer que je n'ai pas d'actions chez Wolfram Research. Je suis seulement persuadé que le concept de programmation va évoluer au fil du temps et que le langage Wolfram est le prélude à changement radical. Il suffit d'ailleurs de le comparer au langage proposé par Maple pour mesurer l'évolution du concept en question sur les 30 dernières années. -
Pourquoi les séquences de 4 chiffres sont les plus fréquentes dans un cas, et ce sont les séquences de 5 chiffres dans un autre cas ?
Attention, on ne calcule pas les séquence les plus fréquentes.
On prend une succession de 50 lancers, et on garde la plus longue séquence de 0 dans le process 1, ou la plus longue séquence sans changement dans le process 2.
Pour une succession de 50 lancers, quand je garde la plus longue séquence de 0 (process 1), ou quand je garde la plus longue séquence sans changement (process 2), j'ai l'assurance que le nombre renvoyé par le process 2 sera au moins égal au nombre renvoyé par le process 1.
Et si par hasard le nombre renvoyé par le process 1 est petit (plus longue séquence de 0 contient seulement 2 ou 3 ou 4 chiffres), j'ai de grandes chances que la plus longue séquence de 1 soit longue (si il y a peu de 0 dans mon tirage, alors il y a beaucoup de 1 !)
Donc, le fait que le process 2 renvoie des nombres plus grands que le process 1, c'était totalement prévisible.
Dans le process 1, avoir 0 comme longueur de la plus longue séquence, c'est rarissime, mais c'est possible. Dans le process 2, c'est impossible.
Par contre, avec des considérations simples comme celles-ci (=du bon sens, de la logique), il est impossible d'anticiper des résultats numériques.
Il faut faire des calculs précis (soit des simulations, soit des calculs théoriques) pour constater que 5 devient plus probable que 4 avec le process 2, alors qu'il est moins probable que 4 avec le process 1.
Si au lieu de prendre des successions de 50 tirages, tu refais la simulation avec des successions de 15 ou 20 tirages, tu vas peut-être constater que c'est 4 la valeur la plus fréquente avec le process 1 et aussi avec le process 2. Mais la courbe donnée par le process 2 sera de toutes façons ""plus-à-droite"" que la courbe donnée par le process 1.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Wilfrid a écrit:lorsqu'on ne différencie pas les 0 et les 1, ce qui paraît totalement contrintuitif ?
on se focalise uniquement sur l'objectif à atteindre, tout comme comme on le fait pour construire un objet
Lorsqu on ne différencie pas les 0 et les 1, c'est au contraire totalement intuitif. Je suppose que tu dirais qu il est totalement contre intuitif de fabriquer le mot 0011 plus vite que le mot 1111 ? Et bien, Markov comme Penney ont prouvé le contraire.
En revanche (pour moi qui n y connaît rien), je suis très sensible à ton argument sur l'objectif à atteindre s'agissant du choix du langage informatique. -
Merci pour ta réponse !lourran a écrit:Si au lieu de prendre des successions de 50 tirages, tu refais la simulation avec des successions de 15 ou 20 tirages, tu vas peut-être constater que c'est 4 la valeur la plus fréquente avec le process 1 et aussi avec le process 2. Mais la courbe donnée par le process 2 sera de toutes façons ""plus-à-droite"" que la courbe donnée par le process 1.
Effectivement, si je procède à 10^6 séries de 30 lancés ou moins avec la fonction consec01[] (que tu nommes process 2), la séquence composée de 0 (ou de 1) la plus fréquente est de longueur 4. A partir de 31 lancés elle est de longueur 5 (pourquoi 31 !). Dans le graphe suivant la courbe bleue représente le résultat de 30 lancés, et la courbe orange celui de 50 lancés :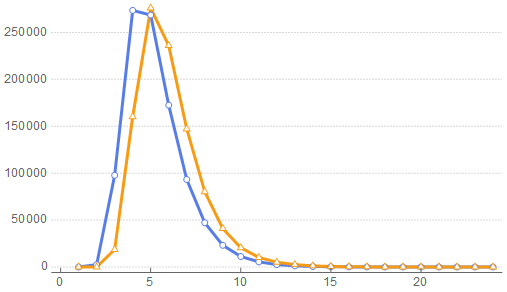 lourran a écrit:Et si par hasard le nombre renvoyé par le process 1 est petit (plus longue séquence de 0 contient seulement 2 ou 3 ou 4 chiffres), j'ai de grandes chances que la plus longue séquence de 1 soit longue (si il y a peu de 0 dans mon tirage, alors il y a beaucoup de 1 !)
lourran a écrit:Et si par hasard le nombre renvoyé par le process 1 est petit (plus longue séquence de 0 contient seulement 2 ou 3 ou 4 chiffres), j'ai de grandes chances que la plus longue séquence de 1 soit longue (si il y a peu de 0 dans mon tirage, alors il y a beaucoup de 1 !)
Ça par contre c'est valable pour une seule série de lancés. Tu appliques ton raisonnement au process 1 (fonction consec0[]) mais il s'applique également au process 2. Sur 10^6 séries, les résultats de 50 lancés composés de plus de 0 que de 1 et ceux composés de plus de 1 que de 0, sont équiprobables. A partir de là il me semble difficile d'expliquer pourquoi on passe de 4 avec 30 lancés à 5 avec 31 lancés, bien que le graphe ci-dessus soit là pour te donner raison sur le fond.
Bref, ce n'est pas intuitif mais ça fonctionne. La preuve en est définitivement apportée par le test d'un nombre de lancés de plus en plus grand (toujours 10^6 séries). Résultats, au format nombre de lancés -> longueur de la séquence la plus fréquente (composée de 0 ou de 1) :
... - 30 -> 4
31 - 61 -> 5
62 - 124 -> 6
125 - 248 -> 7
Ce genre d'expérimentation prend beaucoup de temps, et je n'ai pas envie d'y passer la soirée. Je suppose qu'il existe une formule permettant d'obtenir ces chiffres, non ?jeancreatif a écrit:En revanche ( pour moi qui n y connait rien,) je suis tres sensible à ton argument sur l'objectif à atteindre s'agissant du choix du langage informatique.
Je suis très heureux de l'entendre ! Si on veut entrer dans le futur il va bien falloir qu'on se débarrasse de nos vieilles habitudes ! (:P) -
Dans cette discussion, il y a eu pas mal de réponses à tes questions. (pas dans mes messages :-) ).
Jusque là, la discussion parlait du process 1... pas du process 2.
Pourquoi le passage de 4 à 5 est entre 30 et 31, et pas entre 31 et 32 ... il n'y a pas de raison. l'ordre de grandeur était prévisible intuitivement, mais pas la valeur précise.
Dans la discussion , il y a des gens qui parlent de log en base 2. Ca se retrouve de façon FLAGRANTE dans les chiffres que tu donnes (30 puis 61 puis 24 puis 248).
A chaque fois, on multiplie par 2 environ. On peut donc prédire la ligne suivante de ton tableau :
... - 30 -> 4
31 - 61 -> 5
62 - 124 -> 6
125 - 248 -> 7
249 - 496 ou 497 -> 8
Les valeurs précises ne sont pas intuitives, mais tout le reste, on pouvait parfaitement l'anticiper ; tous ces résultats sont intuitifs.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
@lourran,
Avec des séries de 10^6 lancés la frontière est très ténue entre 4 et 5, 5 et 6, 6 et 7, etc. La conséquence en est que si je lance à nouveau une série de 248 lancés je peux très bien tomber sur une séquence majoritaire de longueur 8, au lieu des 7 précédents. Pour obtenir des valeurs exactes il faudrait passer à un nombre de séries nettement supérieur. Il est donc certain qu'on doit multiplier le nombre limite de lancés par 2 pour passer de 4 à 5, 5 à 6, etc. Il faudrait rechercher le nombre limite exact de lancés pour 4 (voire 2 ou 3), avec 10^10 séries par exemple, mais pour obtenir le résultat rapidement un monstre du type IBM Summit serait nécessaire. -
Ou alors un clonage de 100 IBM +++ (:P)
-
@Wilfrid : on s'écarte du sujet, mais définitivement on n'a pas la même notion de "langage compréhensible". Php m'a toujours parut très confus, et il faut avouer que passer une liste de nombre en chaine de charactère pour faire du comptage n'est pas ce qu'il y a de plus intuitif... Par ailleurs je ne vois pas ton argument comme une différence entre langage mais comme le fait d'utiliser des bibliothèques déjà existantes. Ce que tu fait avec wolfram se fait sans doute très bien avec python ou julia en utilisant les bibliothèques adéquates (et optimisée).
En python :max(len(list(y)) for (c,y) in itertools.groupby(A) if c==0)
donne le nombre de 0 consécutif dans la liste A. Et si on veut le nombre de l'un ou l'autre consécutif :max(len(list(y)) for (c,y) in itertools.groupby(A))
-
@Sylviel,
Personne ne va se livrer à de savants calculs avec Php, c'est un langage de script côté serveur utilisé uniquement pour la programmation de sites Web (notamment l'accès aux bases de données). Je l'ai privilégié pour sa simplicité parce que je m'adressais à ceux qui ne connaissent rien à la programmation.
Tu as raison, convertir une liste en chaine de caractères pour faire du comptage n'est pas l'idéal, mais je n'allais pas perdre mon temps à chercher une solution qui de toute façon n'aurait servi strictement à rien. Mon but était uniquement de comparer les langages séquentiel et procédural (et je n'ai pas manqué de préciser qu'on pouvait faire mieux).
Superbes exemples en Python, vraiment, j'adore ce genre de solution ! Effectivement, tous les langages de programmation proposent des bibliothèques de fonctions qu'il suffit d'installer (avec plus ou moins de facilité). Dans Mathematica le concept de bibliothèque est cependant au cœur du système, on ne peut pas le contourner (on peut même installer des bibliothèques supplémentaires pour faciliter certains calculs particulièrement ciblés). Enfin, de la même manière que lorsque tu construis un objet à l'aide de briques de Lego tu n'as pas besoin d'outils supplémentaires ni de connaissances en bricolage, lorsque tu "programmes" en langage Wolfram tu n'as besoin que de connaissances rudimentaires en programmation, ce qui selon moi est déjà une fameuse évolution, qui va dans le sens où "programmer" une machine deviendra un jour accessible à tout le monde (des tas de gens font de la recherche dans ce domaine. On trouve déjà des petits robots à usage ludique qu'une appli permet de programmer succinctement à l'aide d'une interface simple et intuitive).
Par programmation on entend la manière dont l'homme communique ses instructions aux machines, indépendamment du langage utilisé. A ce titre il est tout à fait envisageable (et j'en suis même persuadé) qu'un autre type de communication soit possible et se mette progressivement en place. Imaginons par exemple une sorte de clavier muni de plusieurs grosses touches : l'ordre dans lequel on en presserait quelques unes – ce qui permettrait un grand nombre de combinaisons –, donnerait instruction à la machine de faire ceci ou cela, sans qu'on ait à se préoccuper de fastidieux détails. Un programme serait alors constitué de séquences de touches, qui formeraient un langage.
@lourran,
C'est bon, on vient de m'installer la lumière au dernier étage. Plus la série de lancés d'une pièce de monnaie est longue et plus le nombre de "pile" consécutifs a des chances d'être grand, d'où l'apparition de séquences majoritaires de longueur 4, 5, 6, ... au fur et à mesure qu'on augmente le nombre de lancés. Donc oui, c'est assez intuitif.
Ce qui me fascine néanmoins est qu'on soit obligés de passer par la simulation pour estimer l'ordre de grandeur desdites longueurs. -
LOU16 écrivait : http://www.les-mathematiques.net/phorum/read.php?43,1869462,1871188#msg-1871188
----Wilfrid, peux tu me dire s'il te plaît, quel langage est celui ci ?
--- ( peut être aucun en particulier... )
[Inutile de reproduire un message présent sur le forum. Un lien suffit. AD] -
@jeancreatif,
Ce n'est pas un langage de programmation mais un outil d'aide à la conception d'un programme, qui représente sa structure, les données à traiter, les méthodes à mettre en oeuvre, le résultat à afficher, bref, une représentation du programme final qui reste à écrire dans un langage quelconque en se basant sur ce modèle. Par exemple, si tu tapes $\text{Afficher}\:\: W[ k ]$ dans Phyton tu auras droit à un message d'erreur, parce que Python ne comprend pas le mot Afficher. Mais si tu tapes print(W[k]) tout se passera bien. "Afficher" signifie seulement que tu dois utiliser l'instruction de sortie correspondante du langage que tu utilises pour visualiser le résultat du calcul, sur ton écran ou autre.jeancreatif a écrit:Je suppose que tu dirais qu'il est totalement contre intuitif de fabriquer le mot 0011 plus vite que le mot 1111 ?
Je ne suis pas certain que c'est ce que je dirais, à moins que tu ne m'expliques de quoi tu parles. -
Merci pour ta réponse Wilfrid.
En effet, s'agissant du mot 0011 qu'on obtient plus vite que 1111, il ne remet pas en cause le fait qu'à chaque lancer "pile" et "face" ont la même probabilité,
(sinon, il y a belle lurette que les casinos auraient supprimé la roulette).
En revanche, si tu les considères comme des mots, alors, fais en l’expérience, et tu verras que 0011 sera obtenu beaucoup plus vite que 1111.
J'ai mis en pièce jointe une chaîne de Markov illustrant ce phénomène (coup de génie de Walter Penney qui l'avait découvert).
0011 sera obtenu avant 1111 dans 75% des cas. -
Je tombe des nues !jeancreatif a écrit:En revanche, si tu considère les considère comme des mots, alors , fais en l'experience, et tu verras que 0011 sera obtenu beaucoup plus vite que 1111.def tests(n=10000): compteur = {"0011":0, "1111":0} for _ in range(n): L = [] while L[-4:]!=[0,0,1,1] and L[-4:]!=[1,1,1,1]: L.append(randint(0,1)) print L compteur["".join(map(str,L[-4:]))]+= 1 return compteur tests(100000)Résultat typique :{'0011': 75073, '1111': 24927} -
C'est normal: un échec dans une tentative de faire 1111 est un échec total (on revient à zéro) alors qu'un échec après 00 ou 001 dans la tentative de faire 0011 n'est qu'un échec partiel (on ne revient pas à zéro).
-
Prenons un exemple un peu plus court ; 011 versus 111.
Dans une succession de lancers, qui arrive (le plus souvent) en premier ? 011 ou 111.
J'ai ma succession de lancers, Je pourrais m'arréter dès que j'ai soit 011, soit 111. Mais je vais choisir de m'arréter uniquement quand j'ai rencontré à la fois 011 et 111.
Et je regarde mon premier 111, il correspond aux lancers n, n+1 et n+2.
Mais il y avait quoi en n-1 ?
Si n =1, la question n'a pas de sens. Si mes 3 premiers lancers sont des 1,alors 111 arrive en premier, et il n.
Si n est différent de 1, alors en n-1, il y avait forcément un 0, sinon j'aurais eu une autre série 111 juste avant la série 111 que je regarde.
Donc soit la série de lancers commence par 111 ( 12.5% des cas ),et j'ai un triplet 111 avant un triplet 011.
Soit la série ne commence pas par 111, et j'ai la certitude que je rencontrerai un 011 avant un 111. (87.5% des cas).
L'exemple cité avec 0011 versus 1111 procède de la même logique... mais en mettant un double 0 en tête de chaine, au lieu d'un simple0, on complique un peu la chose, pour noyer le poisson.
Cette expérience est amusante, mais elle n'a rien à voir avec la question initiale.
Et si on part sur cette expérience, on peut s'amuser.
Je fais n lancers, jusqu'à rencontrer 00110 ou 1111 (volontairement 5 chiffres dans un cas, et 4 dans l'autre). Quel est le groupe de chiffres qui a le plus de chances d'arriver en premier ? Avec quel pourcentage ?
Et comment batir 2 chaines, qui seraient 'aussi favorites l'une que l'autre' à ce jeu mais autres que les cas triviaux (11 versus 00) (donc par exemple en s'imposant 2 chaines de longueurs différentes) ?Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Merci pour vos explications, je n'en ai pas moins été surpris, d'autant que l'espérance du temps d'attente est la même pour les deux fins possibles.
-
Math Coss a écrit:Je tombe des nues !
Là tu vas encore plus tomber des nues.
PF gagne contre FF aussi dans 75% des cas ! -
-
Oui, je me suis souvent demandé comment en faire la démonstration. Et cette page donne des pistes en effet Wilfrid.
-
Dans une succession de lancers, qui arrive (le plus souvent) en premier ? PPFF ou FFFF.
On constate que PPFF arrive en premier 3 fois plus souvent que FFFF (3 fois plus souvent... 75% contre 25% ... ce n'est pas innocent).
On pourrait expliquer ça en disant qu'il y a un équilibre, la pièce doit tomber sur Pile autant de fois que sur Face, et que c'est ça qui explique que FFFF arrive en premier moins souvent que PPFF. C'est le genre de truc qu'on entend. Ce n'est plus des maths mais de l'ésotérisme. Un truc qui dirait qu'à chaque nouveau lancer, la pièce se souvient des résultats précédents, et tendrait à rattraper le retard...
Pour s'en convaincre il suffit de faire une autre expérience. On lance une pièce autant de fois que nécessaire, jusqu'à avoir la séquence FFFF ou FFPP. Et on note laquelle de ces 2 séquences va arriver en premier . FFFF ou FFPP. Et on va constater qu'il y a égalité. Dans 50% des cas la première séquence qu'on rencontre, c'est FFPP, et dans 50% des cas, c'est FFFF.
Dans le match PPFF contre FFFF, PPFF gagne dans 75% des cas
Dans le match FFPP contre FFFF, il y a égalité.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Tu es sûr ? Dans FFPP contre FFFF, l'expérience suivante suggère une répartition 60/40 en faveur de FFPP.
sage: def tests(n=10000): ....: compteur = {"0011":0, "0000":0} ....: for _ in range(n): ....: L = [] ....: while L[-4:]!=[0,0,1,1] and L[-4:]!=[0,0,0,0]: ....: L.append(randint(0,1)) ....: # print L ....: compteur["".join(map(str,L[-4:]))]+= 1 ....: return compteur ....: sage: tests(100000) {'0000': 39832, '0011': 60168} sage: tests(100000) {'0000': 39838, '0011': 60162} sage: tests(100000) {'0000': 39757, '0011': 60243} -
aléa écrivait : http://www.les-mathematiques.net/phorum/read.php?43,1869462,1874646#msg-1874646
[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
Première piste pour une démonstration rigoureuse (que peut-être un surdoué du site saurait faire ...) -
Le diagramme ci-dessous est issu du blog de Wolfram Research, à cette adresse. Il représente les relations entre les 6 séquences toujours gagnantes : PFF, FFP, FPF, PFP, PPF et FPP.
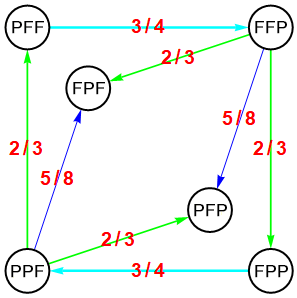
Supposons que je demande à mon adversaire de choisir une des 6 séquences et qu'il opte pour FFP (angle supérieur droit). Mon choix se portera alors sur PFF parce que sa probabilité de gain contre FFP est de 3/4. S'il choisit PFF pas de problème, je prendrai pour ma part PPF (angle inférieur gauche), dont la probabilité de gain contre PFF est de 2/3.
Quel que soit le choix de mon adversaire je sortirai toujours vainqueur de la compétition !jeancreatif a écrit:J'aimerais bien une démonstration de l'inutilité de choisir une façon de miser plutôt qu'une autre ; [...] Et bien tout cela est voué à l'échec.
Il y a peut-être une explication à ça :- Dans une série infinie de lancers toutes les combinaisons de P et de F de longueur donnée sont équiprobables.
$\to$ RAS - Dans le jeu de pile ou face le nombre de lancers est par nature fini.
$\to$ Paradoxe de Penney
- Dans une série infinie de lancers toutes les combinaisons de P et de F de longueur donnée sont équiprobables.
-
@Math Coss
Exact !
J'aurais dû prendre comme exemple FFFF contre FFFP. Ou encore FFFFF contre FFFFP ou même FFFPF contre FFFPP Là, il y a égalité. (Et j'ai vérifié, méfions-nous de notre intuition !)
Il va falloir réfléchir un peu sur la 'combinatoire' qui fait qu'on n'a pas équilibre dans le cas FFFF contre FFPP Mais clairement, ce n'est pas parce que la pièce cherche à rattraper je ne sais quel retard.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Wilfrid tu cites une phrase de moi que j'utilisais pour une autre raison (qui fera l'objet d'une nouvelle conversation ailleurs), celle de l'impossibilité de modifier l’espérance par les différentes répartitions des mises par un joueur (martingales du joueur).
-
-
@jeancreatif,
Je reformule : le paradoxe de Penney énonce ceci : "il est possible de gagner au jeu de pile ou face alors qu'en toute logique on ne le devrait pas". Le "en toute logique" fait référence à une série infinie de lancers, dont intuitivement on sait très bien qu'elle interdit tout gain à ce jeu. Si on admet que dans la vraie vie il est impossible de procéder à une série infinie de lancers, alors il n'y a tout simplement plus de paradoxe. C'est donc nous et nous seuls qui le créons, et le résultat de cette création n'a plus rien à voir avec les probabilités, c'est juste de la combinatoire.
Morale de l'histoire : si tu cherches une explication probabiliste à ce problème tu ne la trouveras pas. -
Bonjour,
Il y a environ six mois, j'avais pour je ne sais plus quel forum fabriqué une procédure en Sagemath qui calcule la chose suivante :
Un joueur choisit une suite A de P ou F
L'autre joueur choisit une suite B de P ou F de même longueur.
On effectue ensuite une suite de tirages à P ou F. Le premier joueur qui voit sa suite sortir a gagné. Quelle est la probabilité que A gagne contre B ? Voici le code# Fabriquer des listes de tirages de longueur voulue def LTPF(n) : if n==0 : return [''] else : L=LTPF(n-1) return ['P'+T for T in L]+['F'+T for T in L] R = PolynomialRing(QQ,'x') # Calcul de la probabilité de victoire en fonction des choix A et B def Prob(A,B) : # liste des tirages à pile ou face de longueur 1 de moins # que A et B L=LTPF(len(A)-1) l=len(L) # Fabrication de la matrice de transition MT=matrix(QQ,l+2,l+2) MT[l,l]=1; MT[l+1,l+1]=1 for i in range(l) : S=L[ i]+'P' if S==A : MT[i,l]=1/2 elif S==B : MT[i,l+1]=1/2 else : MT[i,L.index(S[1:])]=1/2 T=L[ i]+'F' if T==A : MT[i,l]=1/2 elif T==B : MT[i,l+1]=1/2 else : MT[i,L.index(T[1:])]=1/2 # Vecteur d'état initial init=vector(QQ,l+2) for i in range(l) : init[ i]=1/l # Projection sur le sous-espace propre à gauche # associé à la valeur propre 1 Proj=R(MT.minimal_polynomial()/(x-1)) fin=init*(1/Proj(1))*Proj(MT) # Retour des probabilités de victoire pour A et B return fin[l],fin[l+1] # Tableau des probabilités de victoire def TabProb(n) : L=LTPF(n-1) ; M=LTPF(n) l=len(L) ; m=len(M) TP=matrix(QQ,m,m) for i in range(m): for j in range(i) : TP[i,j],TP[j,i]=Prob(M[ i],M[j]) TP[i,i]=1/2 return TP
Puis une exécution pour les suites de longueur 3 et 4print LTPF(3) print TabProb(3) print LTPF(4) print TabProb(4)
avec comme résultat['PPP', 'PPF', 'PFP', 'PFF', 'FPP', 'FPF', 'FFP', 'FFF'] [ 1/2 1/2 2/5 2/5 1/8 5/12 3/10 1/2] [ 1/2 1/2 2/3 2/3 1/4 5/8 1/2 7/10] [ 3/5 1/3 1/2 1/2 1/2 1/2 3/8 7/12] [ 3/5 1/3 1/2 1/2 1/2 1/2 3/4 7/8] [ 7/8 3/4 1/2 1/2 1/2 1/2 1/3 3/5] [7/12 3/8 1/2 1/2 1/2 1/2 1/3 3/5] [7/10 1/2 5/8 1/4 2/3 2/3 1/2 1/2] [ 1/2 3/10 5/12 1/8 2/5 2/5 1/2 1/2] ['PPPP', 'PPPF', 'PPFP', 'PPFF', 'PFPP', 'PFPF', 'PFFP', 'PFFF', 'FPPP', 'FPPF', 'FPFP', 'FPFF', 'FFPP', 'FFPF', 'FFFP', 'FFFF'] [ 1/2 1/2 2/5 2/5 3/10 5/12 4/11 4/11 1/16 3/8 3/8 3/8 1/4 3/8 7/22 1/2] [ 1/2 1/2 2/3 2/3 1/2 5/8 4/7 4/7 1/8 9/16 9/16 9/16 5/12 9/16 1/2 15/22] [ 3/5 1/3 1/2 1/2 3/5 5/7 1/2 1/2 5/12 5/12 9/16 9/16 5/14 1/2 7/16 5/8] [ 3/5 1/3 1/2 1/2 3/7 5/9 2/3 2/3 5/12 5/12 9/16 9/16 1/2 9/14 7/12 3/4] [ 7/10 1/2 2/5 4/7 1/2 1/2 1/2 1/2 7/12 7/12 5/14 1/2 7/16 7/16 7/16 5/8] [ 7/12 3/8 2/7 4/9 1/2 1/2 1/2 1/2 7/16 7/16 1/2 9/14 7/16 7/16 7/16 5/8] [ 7/11 3/7 1/2 1/3 1/2 1/2 1/2 1/2 1/2 1/2 9/16 5/12 7/12 7/12 7/16 5/8] [ 7/11 3/7 1/2 1/3 1/2 1/2 1/2 1/2 1/2 1/2 9/16 5/12 7/12 7/12 7/8 15/16] [15/16 7/8 7/12 7/12 5/12 9/16 1/2 1/2 1/2 1/2 1/2 1/2 1/3 1/2 3/7 7/11] [ 5/8 7/16 7/12 7/12 5/12 9/16 1/2 1/2 1/2 1/2 1/2 1/2 1/3 1/2 3/7 7/11] [ 5/8 7/16 7/16 7/16 9/14 1/2 7/16 7/16 1/2 1/2 1/2 1/2 4/9 2/7 3/8 7/12] [ 5/8 7/16 7/16 7/16 1/2 5/14 7/12 7/12 1/2 1/2 1/2 1/2 4/7 2/5 1/2 7/10] [ 3/4 7/12 9/14 1/2 9/16 9/16 5/12 5/12 2/3 2/3 5/9 3/7 1/2 1/2 1/3 3/5] [ 5/8 7/16 1/2 5/14 9/16 9/16 5/12 5/12 1/2 1/2 5/7 3/5 1/2 1/2 1/3 3/5] [15/22 1/2 9/16 5/12 9/16 9/16 9/16 1/8 4/7 4/7 5/8 1/2 2/3 2/3 1/2 1/2] [ 1/2 7/22 3/8 1/4 3/8 3/8 3/8 1/16 4/11 4/11 5/12 3/10 2/5 2/5 1/2 1/2]
On voit dans le dernier tableau que FFPP a effectivement 3 chances sur 5 de gagner contre FFFF et une chance sur trois de gagner contre FFFP.
Je n'ai pas revérifié ma procédure. -
Wilfrid, selon moi tu ne poses pas bien le problème. De plus je ne cherche pas une explication probabiliste, mais une démonstration rigoureuse exposant la nécessité mathématique qui donne ces résultats.
-
jeancreatif a écrit:Wilfrid, selon moi tu ne poses pas bien le problème.
C'est tout à fait possible. -
Wilfrid
Tu sais, ici, c'est vraiment l'endroit du cerveau collectif il me semble, chacun apporte sa pierre et éveille l'autre. (Dans les centre de recherche américains, se trouvent parfois plusieurs prix Nobels côte à côte, ou tout au moins plusieurs pointures). -
Je me demandais pourquoi FFFF perdait contre FFPP, mais en fait c'est très simple. Ca se joue dès les premiers lancers. Un bon footing, rien de tel pour remettre les idées en place.
En 4 lancers, ces 2 séquences ont chacune 1 chance sur 16 de se produire. Lapalissade. Egalité.
En exactement 5 lancers, FFFF gagnera uniquement dans la configuration PFFFF, alors que FFPP va gagner dans les 2 configurations PFFPP et FFFPP. FFPP est déjà nettement en avance.
Et là, on peut peut-être avancer une première conjecture : Si au bout de $n_0$ lancers, une séquence A a une probabilité supérieure à une séquence B, alors, pour $n_1> n_0$ lancers, A gardera forcément une probabilité supérieure à B.
Et même, une autre conjecture un peu plus forte : Si au bout de $n_0$ lancers, une séquence A a une probabilité $p(n_0)$ supérieure à la probabilité $q(n_0)$ de la séquence B, alors, pour $n_1> n_0$ lancers, le rapport $\frac{p(n_1)}{q(n_1)}$ sera supérieur ou égal au rapport $\frac{p(n_0)}{q(n_0)}$ ; en d'autres mots : l'avance prise par la séquence A ne peut pas se réduire. (c'est une conjecture...pas une certitude)
En tout cas, sur notre cas FFFF versus FFPP, dès le 5ème lancer, on a 3 chances sur 32 que FFFF soit apparu, contre 4 chances sur 32 pour FFPP.
Et dès le 6ème lancer, on a 8 chances sur 64 d'avoir vu FFFF contre 11 chances sur 64 d'avoir vu FFPP. Le rapport 8/11 est déjà très proche du rapport final 40/60.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Sur cette page :http://www.madore.org/~david/math/proba.html voir le sujet : "Un singe et une machine à écrire"
-
lourran tu devrais faire des footings plus souvent(:P) ça te réussit on dirait...
-
Math Coss écrivait:
]Je tombe des nues ![/url]
>
et maintenant le top pour Math Coss : ( roulement de tambours)
FFPP gagne contre PPP dans 58% des cas! -
Merci pour le lien Cidrolin, tout ça m'a l'air bien intéressant.
En fait, je cherchais un mot pour résumer ces questions/ces paradoxes, et je pense que le bon mot, c'est cannibalisation.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Deux joueurs A et B s'affrontent. Le choix d'une séquence de longueur 3 (et uniquement dans ce cas) est laissé à A. Quelle séquence B doit-il choisir pour l'emporter sur A ?
Si A choisit $a_1\,a_2\,a_3$ alors B doit choisir $\dfrac{1}{a_2}\,a_1\,a_2$
où $\dfrac{1}{a_2}$ signifie bien sûr P si F et F si P.
Existe-t-il un algorithme similaire applicable à des séquences plus longues, voire un algorithme universel ?
Source (en anglais) -
A a choisi $ ( a_{i, i=1 à n} ) $
ma proposition : B doit choisir $ ( \frac{1}{a_n-1}, a_{i, i=1 à n-1} ) $
Pourquoi cette proposition ?
1. cohérent avec la solution pour des séquences de longueur 3.
2. Pas/peu de cannibalisation : dans la séquence jouée par B, le premier et le dernier caractère sont différents, et ça semble être un critère ben utile.
3. Quand la séquence de A arrive, il y a 50% de chance que la séquence de B soit sortie juste avant ! Ca limite quand même beaucoup les espoirs de A.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
@lourran,
Pourrais-tu fournir un exemple avec B=FFPP gagnant contre A=PPPP, éventuellement sans faire intervenir les probabilités de gain de B (qu'on peut toujours calculer ultérieurement) ? Ce dont je parlais est d'un algorithme permettant de permuter les lettres de A pour obtenir la séquence gagnante de B. Les chances qu'il a de gagner sont sans importance puisqu'elles dépendent du choix de A, ce qui veut dire que B n'a pas le choix de ses gains (à condition bien sûr qu'il n'existe qu'une seule séquence gagnante). -
FFPP gagne contre PPPP, mais à peu près toutes les combinaisons gagnent contre PPPP. La règle que je propose dit que contrre PPPP, il faut jouer FPPP. Et coup de chance ou pas, FPPP gagne 15 fois sur 16 contre PPPP, c'est la combinaison qui fait le meilleur score contre PPPP.
La 'permutation' que je propose n'est pas claire ? Je détaille.
Supposons qu'on joue avec ds combinaisons de $n$ éléments. A donne donc une succession de n lettres P ou F.
B garde les $n-1$ premières lettres de A, mais ça devient les $n-1$ dernières lettres de la combinaison de B. En gardant le même ordre bien sûr.
exemple : PPPFFX devient YPPPFF
X : X est le dernier symbole choisi par A, ça peut être P ou F, peu importe, ça ne changera rien à la combinaison jouée par B.
Y : B fait en sorte que la 1ère lettre de sa combinaison soit différente de sa dernière lettre. Donc comme sa combinaison finit par F dans cet exemple, il va mettre un P au début. Résultat : PPPPFFTu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




