Un modèle pour Syracuse

Voilà qui aura probablement éclairé la lanterne de Kranom. Aux probabilités qu'il évoquait on lui oppose de pures suppositions ! Et en plus il remercie !

@raoul.S,

Il est inutile de lire l'entièreté du document que tu cites, parce qu'un problème apparaît dès le début. L'auteur note un cycle de cette manière :

$a_1 \rightarrow a_2 \rightarrow \ldots \rightarrow a_N \rightarrow a_1$

où les $a$ forment "la liste de ses éléments distincts deux à deux, dans leur ordre d’apparition sur la trajectoire de $a_1$". Les trois lignes suivantes suggèrent qu'il est question d'une suite standard, dans laquelle les éléments pairs et impairs apparaissent.

A aucun moment il n'est question de la divisibilité de $a_1$ par 3, ce qui pourtant est la condition sine qua non de l'apparition d'un cycle. Si $a_1$ est un multiple impair de 3 (s'il est pair ça n'a aucune incidence), la notation ci-dessus est erronée parce qu'il ne peut pas se retrouver en dernière position (il n'a aucun prédécesseur). L'auteur construit donc son raisonnement sur l'idée implicite que $a_1$ n'est pas un multiple impair de 3. C'est ce qu'on appelle un a priori.

Je ne vais pas répéter les explications que j'ai déjà fournies dans ce message, mais ce qui en ressort est que le raisonnement de ce monsieur peut être contredit sans même faire de mathématiques.

Une telle mauvaise foi dépasse l'entendement. Si je parle de mauvaise foi c'est parce que je pars du principe que vous êtes des garçons intelligents et que vous comprenez à quel paradoxe je fais allusion, et que de plus vous avez lu le message dont j'ai donné le lien plus haut (quoique la question de lourran à propos de 1001 me fait sérieusement douter que ce soit le cas).

Bon, j'abandonne.

@raoul.S, tu peux mettre des $m$ et des $nm$ n'importe où, les relier par des flèches orientées n'importe comment, ça restera toujours du n'importe quoi.

Pour éviter d'être à nouveau piégés dans un vortex on va cette fois-ci rester en ligne droite et se pencher sur le cycle $a_1 \rightarrow a_2 \rightarrow a_3 \rightarrow a_1\,$, en admettant qu'il peut avoir n'importe quelle longueur.

Dans la figure ci-dessous, les $p_i\,, q_i\,, r_i$ sont les prédécesseurs respectifs des $a_i$ (il n'y en a pas que trois mais une infinité). Les multiples de 3 sont en rouge. Le fait qu'ils soient placés en 1ère, 2ème et 3ème position n'est qu'une des représentations possibles.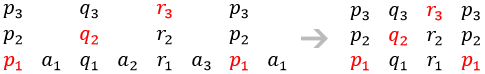



On peut supprimer les $a_i$ et noter le cycle $p_i \rightarrow q_i \rightarrow r_i \rightarrow p_i$. En effet, chaque terme d'une suite impaire appartient à l'ensemble des prédécesseurs de son successeur. Chacun de ces ensembles est ici représenté par une colonne de lettres. Ce sont en réalité des sous-ensembles de l'ensemble des entiers naturels impairs. On pourrait les nommer respectivement $P, Q, R$. Ainsi, $a_1$ appartient à $Q$, $a_2$ à $R$, etc. Le successeur unique de $p_i$ est $q_1$ ou $q_3$ ; celui de $q_i$ est $r_1$ ou $r_2$ ; celui de $r_i$ est $p_2$ ou $p_3$.

Supposons que le premier terme du cycle soit $\color{red}{p_1}$. Comme il n'a pas de prédécesseur il ne peut pas être le successeur de $r_i$. Disons que le successeur de $r_i$ est $p_2$ (ou $p_3$) : aucun cycle ne peut se former puisque $p_2 \ne p_1$. Il n'existe donc pas de cycle débutant par un multiple de 3.

Un cycle possible serait $p_2 \rightarrow q_3 \rightarrow r_1 \rightarrow p_2\,$, mais il pose un sérieux problème. Une suite impaire de Collatz peut être représentée par un chemin traversant une juxtaposition d'ensembles infinis et uniques (les ensembles de prédécesseurs, voir figure ci-dessous), chacun de ses termes appartenant à l'un d'eux. Si un cycle existait il faudrait que l'un de ces ensembles ait été dupliqué, en l'occurrence $P$. C'est la condition sine qua non de l'apparition d'un cycle. Or, l'idée que ce soit le cas d'un seul ensemble bien particulier ne tient pas debout. Si cette duplication était possible elle ne serait pas le fruit du hasard mais obéirait à une règle précise ; une infinité de cycles apparaîtraient alors à intervalle identifiable, de manière parfaitement structurée. J'expliquerai dans le message suivant pourquoi ces ensembles ne peuvent pas être dupliqués.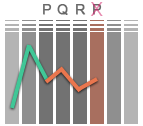



Pour en revenir à Shalom Eliahou, je serais tenté de faire le parallèle entre l'article dans lequel il montre qu'un cycle doit avoir au moins 17 milliards de termes, et la démonstration que la somme des entiers naturels est -1/12. Si le raisonnement tient la route dans les deux cas, sa conclusion est fausse. En supposant qu'une duplication soit possible, qu'elle intervienne après 17 milliards d'étapes n'a strictement aucun sens.

llorteLEG a écrit:

On tourne vite en rond avec Syracuse !

On tounerait en rond s'il existait un cycle. Ne mésestime surtout pas le problème de Collatz, parce qu'il est comme les ovnis : on peut s'y intéresser sans le crier sur les toits.

raoul.S a écrit:

à aucun moment dans ton raisonnement tu utilises la fait que les nombres manipulés sont positifs.

Les suites négatives sont une invention postérieure à Collatz. Je m'intéresse au problème 3n+1, pas à ses extensions. S'il y a quelque chose qui t'échappe dans mes précédents messages, voici une illustration de ce que je disais.

$n$ est un terme d'une suite impaire de Collatz. $P$ est l'ensemble infini des prédécesseurs de $n$. La figure ci-dessous représente la suite 257285, 48241, 36181, 53, 5, 1 :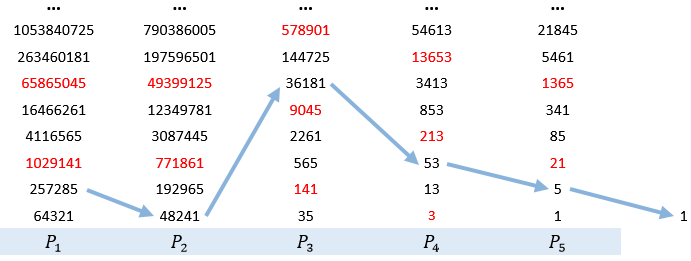

• Les éléments de $P$ sont les $k_i$.
• $P_i$ ne possède qu'un seul et unique successeur, qui est l'élément $k_j$ de $P_{i+1}$. Ceci entraîne que deux éléments $k_i$ et $k_j$ de $P_i$ ne sont pas précédés du même $P_{i-1}$.
• Chaque $P_i$ est unique (distinct des autres) et ne peut pas être dupliqué, ni même partager un seul de ses éléments avec un autre ensemble (j'ai expliqué pourquoi dans mon précédent message).

Considérons les nombres $k_1, k_2, k_3$ appartenant respectivement à $P_1, P_2, P_3\,$, et le cycle $k_1 \to k_2 \to k_3 \to k_1$. Étant donné que $k_1$ appartient à $P_1$ il ne peut en aucun cas appartenir à $P_4$. Ce cycle n'existe donc pas. Le concept de cycle étant fondé sur ce principe, il n'existe aucun cycle.

Essaie de lister l'ensemble des prédécesseurs de chaque terme de la suite ci-dessus et d'appliquer ton argument

Quelle fonction utilises-tu dans le cas d'une suite négative ?

@gerard0,

Imagine qu'un type prétende avoir démontré que le soleil se lève à l'ouest. Comme tu crois qu'il se lève à l'est tu vas chercher à éliminer ce contradicteur, en le décrédibilisant ou en relativisant son discours. Comment vas-tu t'y prendre ? Par exemple en lui répondant : "Très bien, mais à aucun moment vous ne parlez de Vénus, et là-bas il se lève à l'est !".