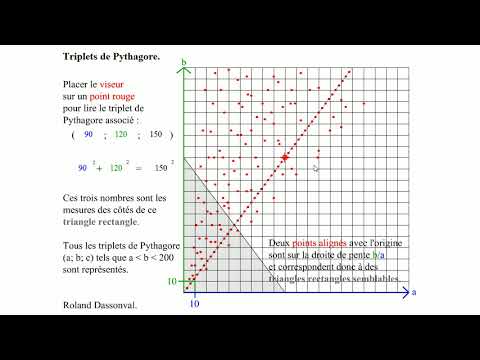
Triplets pythagoriciens

Oui et oui.

Bonjour Elem et bienvenue.

Je confirme ce qu'Eric - que je salue - vient d'écrire.

e.v.

Peut être utile

Bonjour,

@Eric : Montrer que si $\displaystyle x,y,z$ est un triplet pythagoricien primitif, alors $\displaystyle 60|xyz.$

Comme $\displaystyle 60=2^2.3.5$ il suffit de montrer que $\displaystyle 2^2|xyz$ et $3|xyz$ et $5|xyz.$

On sait qu'il existe des entiers relatifs $\displaystyle u,v$ tels que $\displaystyle xyz=2uv(u^2-v^2)(u^2+v^2).$ On construit alors des tableaux de congruences pour montrer que : $\displaystyle 2^2|2uv(u^2-v^2)(u^2+v^2)$ et $\displaystyle 3|2uv(u^2-v^2)(u^2+v^2)$ et $\displaystyle 5|2uv(u^2-v^2)(u^2+v^2).$ Voilà !

Par exemple, pour la congurence $5$ :
$\displaystyle \begin{pmatrix} u:&0&1&2&3&4 \\ u^2:&0&1&4&4&1 \end{pmatrix}.$
$\displaystyle \begin{pmatrix} uv&0&1&2&3&4 \\ 0&0&0&0&0&0 \\ 1&0&1&2&3&4 \\ 2&0&2&4&1&3 \\ 3&0&3&1&4&2 \\ 4&0&4&3&2&1\end{pmatrix}$ $\displaystyle \begin{pmatrix} u^2+v^2&0&1&4&4&1 \\ 0&0&1&4&4&1 \\ 1&1&2&0&0&2 \\ 4&4&0&3&3&0 \\ 4&4&0&3&3&0 \\ 1&1&2&0&0&2\end{pmatrix}$ $\displaystyle \begin{pmatrix} u^2-v^2&0&1&4&4&1 \\ 0&0&4&1&1&4 \\ 1&1&0&2&2&0 \\ 4&4&3&0&0&3 \\ 4&4&3&0&0&3 \\ 1&1&0&1&1&0\end{pmatrix}$
et on calcule que la table de $\displaystyle uv(u^2-v^2)(u^2+v^2)$ ne contient que des $0$ : cette quantité est divisible par $5.$

On peut faire ça directement à coup de congruences, ou bien utiliser les propriétés suivantes :

Si $(a,b,c)$ un triplet pythagoricien primitif, alors
un et un seul des entiers $a$ ou $b$ est pair et donc divisible par~$4$;
un et un seul des entiers~$a$ ou~$b$ est divisible par~$3$;
un des entiers $a$, $b$ ou $c$ est divisible par~$5$.

Le plus efficace est certainement de procéder comme Yves.