Nombres premier -3 = somme des différences.

Je plagie ce que vient de dire Poirot avec moins de formalisme [\begin{array}{rcl}
\text{différence}&&\text{sommes partielles}\\
{\color{purple}{3-2}}=1&\quad&\\
{\color{blue}{5-3}}=2&&{\color{blue}{5-3}}+{\color{purple}{3-2}}=5-2\\
{\color{teal}{7-5}}=2&&{\color{teal}{7-5}}+{\color{blue}{5-3}}+{\color{purple}{3-2}}=7-2\\
{\color{green}{11-7}}=4&&{\color{green}{11-7}}+{\color{teal}{7-5}}+{\color{blue}{5-3}}+{\color{purple}{3-2}}=11-2\\
{\color{olive}{13-11}}=2&&{\color{olive}{13-11}}+{\color{green}{11-7}}+{\color{teal}{7-5}}+{\color{blue}{5-3}}+{\color{purple}{3-2}}=13-2\\
{\color{lime}{17-13}}=4&&{\color{lime}{17-13}}+{\color{olive}{13-11}}+{\color{green}{11-7}}+{\color{teal}{7-5}}+{\color{blue}{5-3}}+{\color{purple}{3-2}}=17-2\\
\text{etc.}\end{array}\]

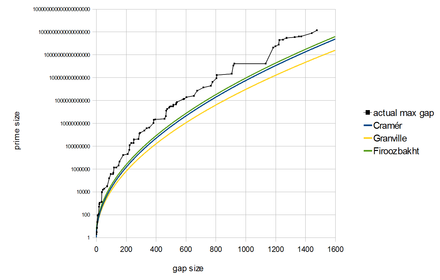
Si ${\displaystyle p_{n}}$ est le n-ième entier premier, le n-ième écart est : ${\displaystyle g_{n}=p_{n+1}-p_{n}}$ soit : ${\displaystyle p_{n+1}=2+\sum _{i=1}^{n}g_{i}}$ . On a ${\displaystyle g_{n}<p_{n}}$ et ${\displaystyle g_{n}}$ devient de l'ordre de ${\displaystyle \log(n)}$

En fait ça revient au même que ce qui est dit avec $2$. Ca donne $p_n - 3$. Je pensais qu'il voulait estimer $p_{n+1}$ connaissant tous les premiers jusqu'à $p_n$. Il n'en est rien.