Divergence ou convergence ?
dans Arithmétique
Salut.
Ces 4 séries $a, b, c$ et $d$ convergent elles ? Sachant que $\zeta(1)$ diverge.
$\zeta(1)=a + b + c + d$ $$
\zeta(1)=\sum_{k=1}^\infty{\frac1{4k-3}}+\sum_{k=1}^\infty{\frac1{4k-2}}+\sum_{k=1}^\infty{\frac1{4k-1}}+\sum_{k=1}^\infty{\frac1{4k}}
$$ En fait je découvre un peu les séries.
J'ai découvert que $\exp(\mathrm ix) = \cos(x)+\mathrm i\sin(x)$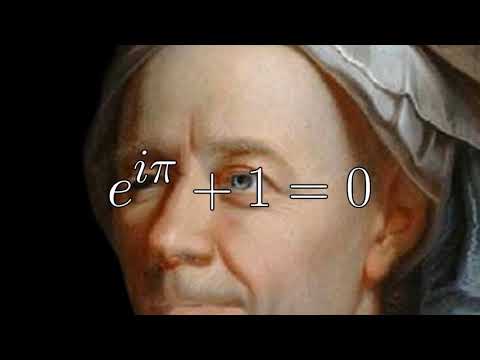
puis en me promenant sur wikipedia je suis tombé sur le développement en série du logarithme. https://fr.wikipedia.org/wiki/Logarithme_naturel#Développement_en_série
Naïvement j'ai voulu faire comme Euler pour $\exp(\mathrm ix)$ mais avec le logarithme que je trouve assez proche de $\zeta(1)$. $$
\ln(1 + ix)=i\sum_{k=1}^\infty{\frac1{4k-3}}+\sum_{k=1}^\infty{\frac1{4k-2}}-i\sum_{k=1}^\infty{\frac1{4k-1}}-\sum_{k=1}^\infty{\frac1{4k}}.
$$ Edit : n k
Ces 4 séries $a, b, c$ et $d$ convergent elles ? Sachant que $\zeta(1)$ diverge.
$\zeta(1)=a + b + c + d$ $$
\zeta(1)=\sum_{k=1}^\infty{\frac1{4k-3}}+\sum_{k=1}^\infty{\frac1{4k-2}}+\sum_{k=1}^\infty{\frac1{4k-1}}+\sum_{k=1}^\infty{\frac1{4k}}
$$ En fait je découvre un peu les séries.
J'ai découvert que $\exp(\mathrm ix) = \cos(x)+\mathrm i\sin(x)$
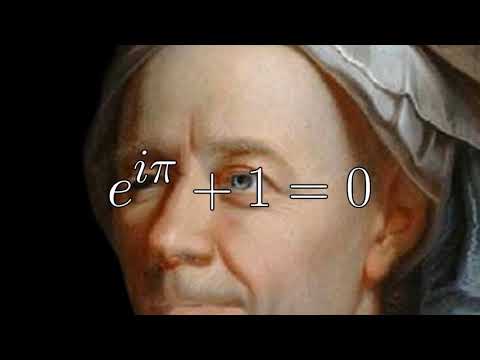puis en me promenant sur wikipedia je suis tombé sur le développement en série du logarithme. https://fr.wikipedia.org/wiki/Logarithme_naturel#Développement_en_sérieNaïvement j'ai voulu faire comme Euler pour $\exp(\mathrm ix)$ mais avec le logarithme que je trouve assez proche de $\zeta(1)$. $$
\ln(1 + ix)=i\sum_{k=1}^\infty{\frac1{4k-3}}+\sum_{k=1}^\infty{\frac1{4k-2}}-i\sum_{k=1}^\infty{\frac1{4k-1}}-\sum_{k=1}^\infty{\frac1{4k}}.
$$ Edit : n k
Réponses
-
Tes quatre séries divergent. Leur terme général est équivalent à $\frac{1}{4n}$, qui est le terme général d'une série divergente (série harmonique).
Tu peux même le prouver à la main, en minorant chacun de tes termes généraux par $\frac{1}{4(n-1)}$ (au moins pour $n \geq 2$). Au passage ton indice de sommation est $n$ mais tu mets des $k$ dans tes sommes. -
$$\ln(1 + ix)=i\sum_{k=1}^\infty{\frac1{4k-3}}-i\sum_{k=1}^\infty{\frac1{4k-1}}+\frac{\ln(2)}{2}.
$$ Il me semble. -
Salut Fly,
Faut vraiment éviter d'écrire des $\sum_{k=1}^\infty u_n$ pour des séries dont la convergence n'est pas assurée. Pourquoi ? Simplement par tu n'es pas Euler et tu risques de faire n'importe quoi (tu as le droit mais faut le savoir, je veux dire ce n'est pas interdit par une loi de faire n'importe quoi !) -
Bonjour Fly7.
Tu peux t'amuser à écrire des formules sans signification, mais tu devrais aumoins leur donner un semblant de cohérence !
Ici : $\ln(1 + ix)=i\sum_{k=1}^\infty{\frac1{4k-3}}-i\sum_{k=1}^\infty{\frac1{4k-1}}+\frac{ln(2)}{2}$
le premier membre varie avec x alors que le second n'en dépend absolument pas !!
NB : les deux séries divergentes du début peuvent se réécrire correctement sous la forme d'une seule série, convergente.
$\sum_{k=1}^n{\frac1{4k-3}}-\sum_{k=1}^n{\frac1{4k-1}} = \sum_{k=1}^n{\frac 2{(4k-3)(4k-1)}}$
Cordialement. -
Exact. $(x=i)$ $$
\ln(1 + i)=i\sum_{k=1}^\infty{\frac1{4k-3}}-i\sum_{k=1}^\infty{\frac1{4k-1}}+\frac{\ln(2)}{2}.
$$ Arg je suis nul en mathématique je ne vois pas comment ça converge je vois juste $$
\sum_{k=1}^n{\frac1{4k-3}}-\sum_{k=1}^n{\frac1{4k-1}} = \sum_{k=1}^n{\frac 2{(4k-3)(4k-1)}}= \frac{\pi^2}{48}+\sum_{k=1}^n{\frac 2{-16k+3}}.
$$ Mais à vue d'œil $\ \displaystyle\sum_{k=1}^n{\frac 2{-16k+3}}\ $ diverge !!
Harg je suis mauvais.
Ha, ça y est, la mémoire me revient https://fr.wikipedia.org/wiki/Pi#Approximation_de_π
$$\ln(1 + i)=\frac{i\pi}{4}+\frac{\ln(2)}{2}.$$
Du coups, je me demande si il est possible de trouver une écriture en gardant la variable x pour $\ln(1 + ix)=?(x)+?(x)$
Tout comme $\exp(\mathrm ix) = \cos(x)+\mathrm i\sin(x)$
Ha, j'ai un début de réponse:
$\ln(1 + ix)=i\arctan(x)+?(x)$
On pourrais être tenter de faire:
$\ln(1 + ix)=i\arctan(x)+\frac{\ln(1 + x)}{2}$ mais sa ne fonctionne que avec x=1 pfff.
Au passage, je vais me faire taper sur les doigt.
$\zeta(1)=\frac{ln(\frac{2}{0})}{2}+\frac{\zeta(1)}{2}$
$\zeta(1)=\frac{1}{3}ln\infty$ -
$\ln(1 + ix)=i\arctan(x)+((\frac{\ln(1 + x)}{2})^2$
Si je ne me trompe.
Car $(a^b)^c = a^{b \times c}.$
Ha ma calculette me fait mentir.
Maintenant il ne me reste plus qu'à trouver une valeur intéressante pour $x$. -
Yes j'ai trouvé.
$\forall x\in\left]-1,1\right[,\quad\ln(1 + ix)=i\arctan(x)+\dfrac{\ln(1 + x^2)}{2}$
Maintenant il ne me reste plus qu'à trouver une valeur intéressante pour $x$ -
Je ne comprends pas ton obstination à écrire des choses qui n'ont pas de sens. Et tu ne réinventes pas l'eau chaude, les manipulations de séries divergentes sont vieilles comme Euler, tandis que les manipulations hasardeuses de logarithmes complexes sont malheureusement faites par la majorité des étudiants de mathématiques. :-D
-
Salut.
"Je ne comprends pas ton obstination à écrire des choses qui n'ont pas de sens."
Parce que tu ne t'es pas posé la question de savoir si ton interlocuteur connaît des choses qui ont du sens.
J'ignore ce qui a du sens pour vous.
Plutôt que de répéter à tous vos interlocuteurs que ce qu'ils font n'ont pas de sens, soumets leurs des propositions qui ont du sens pour vous.
Cordialement,
Thomas. -
Heu ... Thomas,
tu écris sur un forum de mathématiques des écritures qui n'ont pas de sens mathématique. Soit tu ne sais pas ce que sont ces écritures, et un effort léger te permettrait de savoir de quoi il s'agit, soit tu trolles.
Dans les deux cas, ça manque de sérieux. Et c'est toi qui es venu ici poser des questions ... respecte ceux à qui tu demandes de l'aide. -
Tu as un bouquin, Thomas ?
Parce que ce que tu demandes est très très classique, mais c'est vrai que ce n'est pas forcément très évident à inventer tout seul. (c'est un euphémisme)
Tu pourrais regarder un livre de prépa éco première année. Ils font des séries.
Généralement, toutes les classes qui font des probas discrètes doivent généralement faire des séries. -
On t'a expliqué pourquoi ça n'a pas de sens. Tes séries divergent. Tu es en train d'écrire des choses du style $\ln(1+i) = i\infty - i\infty + \frac{\ln 2}{2}$, ça ne veut rien dire.
-
Tu as un bouquin, Thomas ?
Non, je suis un matheux du dimanche.
J'ai fait un BEP en mécanique parce que je suis dyslexique.
Je picore sur wikipedia en espérant un jours lire de maniéré fluide des termes qui ressemblent davantage a du chinois pour le moment.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres
Qui est en ligne 19
+10 Invités