Les classes d'équivalence en application
Bonjour,
j'étudie les classes d'équivalence. Voici les notations introduite dans mon cours.
1. $(G,.)$ un groupe noté multiplicativement
2. $H$ un sous-groupe de $G$.
3. $g R h \Leftrightarrow g^{-1}h\in H$ est une relation d'équivalence
4. $\bar{g}=\{h\in H\mid gRh\}=g.H$ est la classe d'équivalence à gauche modulo $H$
5. $G/H=\{\bar{g}\mid g\in G\}$ est le quotient du groupe $G$ par $H$
6. $G=\bigcup_{i\in I}\bar{g_i}=\bigcup_{g\in G}gH$ est la partition obtenue par les classes d'équivalence.
Je souhaite écrire ce que l'on obtient avec :
1. $(\mathbb{Z},+)$ noté additivement
2. $H=n\mathbb{Z}$ par théorème, les sous-groupes de $\mathbb{Z}$ sont de cette forme
3. $a R b \Leftrightarrow a-b\in n\mathbb{Z}$ est une relation d'équivalence
4. $\bar{a}=\{b\in n\mathbb{Z}\mid aRb\}=a+n\mathbb{Z}$ est la classe d'équivalence de a modulo n.
5. $\mathbb{Z}/n\mathbb{Z}=\{\bar{a}\mid a\in \mathbb{Z}\}$ est le quotient du groupe $\mathbb{Z}$ par $H=n\mathbb{Z}$
6. Je ne vois pas trop quoi écrire.
J'ai un doute sur le point 4.
Et pour le point 5, j'aimerais retrouver le fait que $\mathbb{Z}/n\mathbb{Z}=\{\overline{0},\cdots\overline{n-1}\}$. Dans cet objectif, je ne vois pas comment obtenir l'égalité suivante :
$\mathbb{Z}/n\mathbb{Z}=\{\bar{a}\mid a\in \mathbb{Z}\}=\{a+n\mathbb{Z}\mid a\in \mathbb{Z}\}=\{\overline{0},\ldots,\overline{n-1}\}$.
Pouvez-vous m'aider ?
D'avance merci.
j'étudie les classes d'équivalence. Voici les notations introduite dans mon cours.
1. $(G,.)$ un groupe noté multiplicativement
2. $H$ un sous-groupe de $G$.
3. $g R h \Leftrightarrow g^{-1}h\in H$ est une relation d'équivalence
4. $\bar{g}=\{h\in H\mid gRh\}=g.H$ est la classe d'équivalence à gauche modulo $H$
5. $G/H=\{\bar{g}\mid g\in G\}$ est le quotient du groupe $G$ par $H$
6. $G=\bigcup_{i\in I}\bar{g_i}=\bigcup_{g\in G}gH$ est la partition obtenue par les classes d'équivalence.
Je souhaite écrire ce que l'on obtient avec :
1. $(\mathbb{Z},+)$ noté additivement
2. $H=n\mathbb{Z}$ par théorème, les sous-groupes de $\mathbb{Z}$ sont de cette forme
3. $a R b \Leftrightarrow a-b\in n\mathbb{Z}$ est une relation d'équivalence
4. $\bar{a}=\{b\in n\mathbb{Z}\mid aRb\}=a+n\mathbb{Z}$ est la classe d'équivalence de a modulo n.
5. $\mathbb{Z}/n\mathbb{Z}=\{\bar{a}\mid a\in \mathbb{Z}\}$ est le quotient du groupe $\mathbb{Z}$ par $H=n\mathbb{Z}$
6. Je ne vois pas trop quoi écrire.
J'ai un doute sur le point 4.
Et pour le point 5, j'aimerais retrouver le fait que $\mathbb{Z}/n\mathbb{Z}=\{\overline{0},\cdots\overline{n-1}\}$. Dans cet objectif, je ne vois pas comment obtenir l'égalité suivante :
$\mathbb{Z}/n\mathbb{Z}=\{\bar{a}\mid a\in \mathbb{Z}\}=\{a+n\mathbb{Z}\mid a\in \mathbb{Z}\}=\{\overline{0},\ldots,\overline{n-1}\}$.
Pouvez-vous m'aider ?
D'avance merci.
Réponses
-
Ton 4 est correct. Pour le 5, il faut te convaincre que la classe de $a$ est la classe d'exactement un entier entre $0$ et $n-1$.
Pour 6 tu as déjà tout fait : $\mathbb Z = \bigcup_{k=0}^{n-1} \left(k + n \mathbb Z\right).$ -
Bonjour Poirot,
merci de la réponse.
Dois-je utiliser la division euclidienne ? -
C'est une bonne idée.
-
Je vois.
On fait la division euclidienne de $a$ par $n$, ce qui donne :$a=nq+r,$ avec $0\le r\le n-1$
Donc $a-r=nq$ et donc $\bar{a}=\bar{r}$.
D'où $\mathbb{Z}/n\mathbb{Z}=\{\bar{a}\mid a\in \mathbb{Z}\}=\{\bar{r},\ 0\le r\le n-1\}=\{\overline{0},\ldots,\overline{n-1}\}$.
N'ai-je pas oublié une inclusion réciproque ? -
Oui, là, tu as juste montré $\mathbb{Z}/n\mathbb{Z} \subset \{\bar{0},\ldots,\overline{n-1}\}$. Mais l'autre inclusion ne devrait pas poser de problème (elle est bien plus simple!).
-
Si $u\in\{\overline{0},\ldots,\overline{n-1}\}$ alors on peut écrire $u=\bar{a}$ avec $a\in\{0,\ldots,n-1\}\subset\mathbb{Z}$.
D'où $u\in\mathbb{Z}/n\mathbb{Z}=\{\bar{a}\mid a\in\mathbb{Z}\}$.
Est-ce bien cela ? -
Oui. Ou bien, tout simplement, par définition, les trucs de la forme $\bar{a}$ sont des éléments de $\mathbb{Z}/n\mathbb{Z}$, donc tout ensemble de trucs de cette forme est inclus dans $\mathbb{Z}/n\mathbb{Z}$ :-D.
-
(tu) Merci !
En fait je viens de réaliser que l'on retombe sur des choses simples avec ce type de partition dans ce cas là. Par exemple, si $n=3$ :$\mathbb{Z}=3\mathbb{Z}\cup(3\mathbb{Z}+1)\cup(3\mathbb{Z}+2)$Je voudrais faire le même travail avec le groupe des permutations $S(E)$ muni de la loi interne de composition. La relation d'équivalence étant définie par :
$i R j \Leftrightarrow \exists p\in\mathbb{Z},\ \sigma^p(i)=j$.
Est-ce que je le fais en suivant dans ce fil de discussion, ou est-ce que j'en ouvre un autre ? -
Tu peux continuer ici.
-
Dans ta deuxième relation d'équivalence, qui est $\sigma$?
-
J'ai oublié de préciser, $\sigma\in S(E)$ est une permutation de l'ensemble $E$, c-à-d une bijection de E.
-
Attention, ce que tu as défini est une relation d'équivalence sur $E$, pas sur $\mathfrak S(E)$, donc ce n'est pas le même genre de relation d'équivalence ($E$ n'a aucune raison d'être un groupe, et même si c'est le cas, cette relation n'a aucune raison d'être compatible avec la structure de groupe).
-
Ah oui, il vaudrait donc mieux que je cite ce sur quoi s'applique la relation d'équivalence :
$a\mathcal{R}_G b$ et G est un groupe.
$i\mathcal{R}_E j$ et E est un ensemble, sans être forcément un groupe.
Est-ce que cela change autre chose ? -
Donc, par rapport à mon message initial, 1. et 2. n'ont pas lieu d'être.
Je passe directement au 3. Il s'agit de prouver la symétrie, la réflexivité et la transitivité.
- $i\mathcal{R}_E i$ avec $\sigma=Id_E$.
- Si $i\mathcal{R}_E j$ alors $\exists p\in\mathbb{Z},\ \sigma^p(i)=j \Rightarrow i=\sigma^{-p}(j)$ (en effet, $\sigma$ étant bijective d'inverse $\sigma^{-1}$ alors $\sigma^p$ l'est aussi d'inverse $\sigma^{-p}$.
Ce qui prouve que $j\mathcal{R}_E i$
- Si $i\mathcal{R}_E j$ alors $\exists p\in\mathbb{Z},\ \sigma^p(i)=j $
Si $j\mathcal{R}_E k$ alors $\exists q\in\mathbb{Z},\ \sigma^q(j)=k$
D'où $\sigma^q(j)=\sigma^q(\sigma^p(i))=\sigma^{p+q}(i)=k$ et donc $i\mathcal{R}_E k$.
C'est donc bien une relation d'équivalence.
Qu'en pensez-vous ? -
Pour la réflexivité tu as soudainement choisi un $\sigma$ particulier, pourtant dans la définition de ta relation $\mathcal R_E$, $\sigma$ est fixé, il y a donc une erreur que je te laisse corriger.
-
Ah oui, c'est plutôt :
$i\mathcal{R}_Ei$ puisqu'il existe $p=0$ de sorte que $\sigma^p(i)=i$. -
Pour le point 4., je trouve :
$\bar{i}=\{j\in E|i\mathcal{R}_Ej\}=\{j\in E\,|\,\exists p\in\mathbb{Z}\,|\,\sigma^p(i)=j\}$
Puis-je aller plus avant dans le description de la classe $\bar{i}$ ? -
Pas vraiment. Tu peux réécrire $\bar{i} = \{\sigma^p(i) \mid p \in \mathbb Z\}$ pour une écriture alternative. Si tu sais que $\sigma$ est d'ordre fini (automatique si $E$ est fini), il existe un plus petit entier $d \geq 1$ tel que $\sigma^d(i)=i$ et donc $\bar{i} = \{i, \sigma(i), \dots, \sigma^{d-1}(i)\}$.
-
Merci.
Pour le point 5, l'écriture G/H n'as pas non plus lieu d'être.
Par contre, je peux toujours "quotienter" l'ensemble E par la relation d'équivalence $\mathcal{R}_E$, mais comment le noter ? -
On note $E/\mathcal R_E$ en général.
-
Je vois.
Alors le point 5 s'écrit dans le cas présent :
$E/\mathcal{R}_E=\{\bar{i}\,,i\in E\}$
Si $E$ est infini, alors je ne pense pas pouvoir simplifier cette écriture.
Si $E=\{1\,,\cdots\,,n\}$ alors je peux écrire $E/\mathcal{R}_E=\{\bar{1}\,,\bar{2}\,,\cdots\,,\bar{n}\}$.
Ce qui ressemble fortement à $\mathbb{Z}/n\mathbb{Z}=\{\bar{0}\,,\bar{1}\,,\cdots\,,\overline{n-1}\}$.
Est-ce qu'il existe un lien entre les deux ?
Peut-on, là aussi, simplifier l'écriture de cet ensemble ? -
Si $E = \{1, \dots, n\}$, $\sigma$ est un élément du groupe symétrique $\mathfrak S_n$ des permutations de $E$, et admet une décomposition en produit de cycles à supports disjoints : $$\sigma = (a_{1,1} \, a_{1, 2} \, \dots \, a_{1, l_1}) \dots (a_{r,1} \, \dots \, a_{r, ir}).$$ Alors $$E/\mathcal R_E = \{\overline{a_{1,1}}, \dots, \overline{a_{r,1}}\}.$$ Bon en disant ça on tourne en rond, puisque les cycles de $\sigma$ sont décrits par les orbites de son action sur $E$, donc tout ça revient au même.
-
Merci Poirot.
Je connaissais ce théorème.
Mais il me semble que pour le démontrer, on utilise justement une partition de l'ensemble E par les classes d'équivalence, non ? -
Oui, c'est pour ça que je dis qu'on tourne en rond !
-
Je reviens aujourd'hui sur la notion de classe d'équivalence. Et je me rends compte que le point 6 n'est pas clair.
Avec les notations classiques, je veux montrer le théorème de Lagrange, à savoir que :$card(G)=card(G/H)\times card(H)$
Pour cela, j'ai besoin d'écrire que $\large G=\cup_{\bar{g}\in G/H}\bar{g}$. (réunion disjointe)
Puisque la classe d'équivalence $\bar{g}$ est égal à l'ensemble $g.H$ et que ce dernier a la même nombre d'éléments que $H$, je trouve ainsi que :$\begin{aligned}
card(G)&=\sum_{\bar{g}\in G/H}card(\bar{g})\\
&=\sum_{\bar{g}\in G/H}card(gH)\\
&=\sum_{\bar{g}\in G/H}card(H)\\
&=card(H)\sum_{\bar{g}\in G/H}1\\
&=card(H)card(G/H)
\end{aligned}$
Ma question porte sur la réunion.
Dans de nombreux documents je vois l'écriture $\large E=\cup_{x\in E}\bar{x}$.
J'ai aussi vu l'écriture : $\large E=\cup_{C\in E/\mathcal{R}} C$.
J'ai vu une autre écriture du style : $\large G=\cup_{i\in I} \bar{g_i}$.
Et, dans le cas présent, moi j'écris : $\large G=\cup_{\bar{g}\in G/H}\bar{g}$.
Je ne m'y retrouve pas trop avec ces différentes notations. Sur le site de Christophe Bertault, je trouve cette illustration très parlante avec l'idée qu'avoir la même classe d'équivalence s'exprime en français par "avoir le même ...". Par exemple, avoir le même signe, avoir le même reste, etc.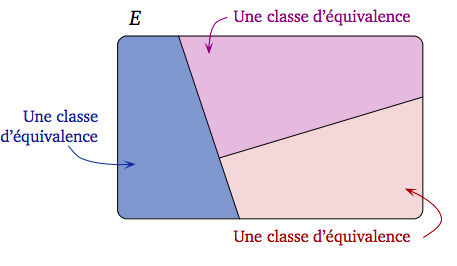
Mais je n'arrive pas à relier ces illustrations et ces idées, avec les bonnes notations. Pouvez-vous m'aider ?
D'avance merci ! -
Toutes les notations données sont correctes, dans le bon contexte.
$$\large G=\cup_{\bar{g}\in G/H}\bar{g}$$ n'a pas besoin de contexte, et la réunion est disjointe.
L'écriture $$\large G=\cup_{g\in G}\bar{g}$$ est également correcte, mais la réunion n'est pas disjointe, il y a des "répétitions". Si $g$ et $g'$ sont en relation (dans ce contexte ça veut dire que $gg'^{-1} \in H$) alors $\bar{g} = \bar{g'}$.
L'écriture $$\large G=\cup_{i\in I} \bar{g_i}$$ correspond certainement au cas où l'on a choisi un représentant (et un seul) $g_i \in G$ de chaque classe d'équivalence dans $G/H$. Dans ce cas, c'est exactement la même chose que $\large G=\cup_{\bar{g}\in G/H}\bar{g}$ sauf que la réunion est indexée par des éléments de $G$ plutôt que par les éléments de $G/H$, ce qui peut être utile dans certaines situations.
Ces trois écritures peuvent se généraliser sans problème au cas d'une relation d'équivalence $\mathcal R$ quelconque sur un ensemble $E$. Il faut simplement comprendre qu'une relation d'équivalence sur $E$, c'est la même chose qu'une partition de $E$, ça veut juste dire que l'on regroupe par "paquets" les éléments de $E$, en général suivant la fait qu'ils partagent une propriété intéressante, par exemple avoir le même reste modulo $n$, vérifier $gg'^{-1} \in H$. ;-) L'ensemble quotient $E/\mathcal R$ c'est alors juste l'ensemble des paquets ! -
Merci Poirot.
Je vais prendre l'exemple plus concret de $G=\mathbb{Z}$, $H=3\mathbb{Z}$ et $G/H=\{\bar{0},\bar{1},\bar{2}\}$.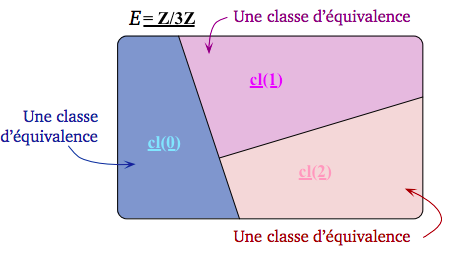
Je peux écrire :
$\large G=\cup_{\bar{g}\in G/H}\bar{g}\iff \mathbb{Z}=\cup_{\bar{g}\in\mathbb{Z}/3\mathbb{Z}}\bar{g}=\bar{0}\cup\bar{1}\cup\bar{2}$, c'est une union disjointe.
Mais je peux aussi écrire :
$\large G=\cup_{g\in G}\bar{g}\iff \mathbb{Z}=\cup_{g\in \mathbb{Z}}\bar{g}=\cdots\cup\bar{-1}\cup\bar{1}\cup\bar{0}\cup\bar{1}\cup\bar{2}\cup\cdots$, ce n'est pas une union disjointe.
Et enfin :
Dans l'écriture, $\large G=\cup_{i\in I} \bar{g_i}$ et avec cet exemple, il faut comprendre que :
- Je choisis un représentant de chaque classe d'équivalence de G/H. Soit ici $\bar{g_1}=\bar{0}$ ; $\bar{g_2}=\bar{1}$ ; $\bar{g_3}=\bar{2}$.
- J'obtiens un ensemble fini d'indice $I=\{1,2,3\}$
Et alors, on a $\large G=\cup_{i\in I} \bar{g_i}\iff \mathbb{Z}=\cup_{i=1}^3 \bar{g_i}$.
Je pense que c'est beaucoup plus clair ! -
Attention au début de ton message, $G$ c'est $\mathbb Z$, pas $\mathbb Z/3 \mathbb Z$. Et $H$ c'est le sous-groupe $3 \mathbb Z$ de $G$. Sinon tu as l'air d'avoir compris effectivement.
-
C'est rectifié !
Dans un autre exercice, j'avais $G$ un groupe agissant sur un ensemble $X$. Et je devais montrer que pour tout $x$ de $X$, on a :$\mathrm{card}(G)=\mathrm{card}(G_x)\mathrm{card}(G.x)$
$G$ étant un groupe fini, $G_x$ et $G.x$ stabilisateur et orbite de $x$ sous l'action de $G$.
Je l'avais fait dans un autre cadre, mais la démonstration que je viens de voir me déroute un peu. Voici :
On fixe $x\in X$.
On considère l'application $ \begin{array}{lccl}
f : &G &\rightarrow& G.x \\
&g& \mapsto &g.x
\end{array}$.
a) Elle est surjective car si $y\in G.x$, alors il existe $g\in G$ tel que $y=g.x$. Par suite $f(g)=g.x=y$.
b) On remarque que $f^{-1}(\{x\}):=\{g\in G\mid f(g)=x\}=G_x$.
c) Soit $y\in G.x$, alors il existe $\gamma\in G$ tel que $y=\gamma.x$. On constate alors que $g\in f^{-1}(\{y\})\iff g.x=\gamma.x \iff \gamma^{-1}g\in G_x$.
d) On en déduit que $g\in f^{-1}(\{y\})\iff g\in\gamma G_x$.
e) Et c'est à partir de ce point là que je bloque. Je cite :
Pour tout $y\in G.x$, les ensembles $f^{-1}(\{y\})$ ont donc le même cardinal, égal à $\mathrm{card}(G_x)$. Comme ils forment une partition de $G$, la proposition en résulte.
J'ai cherché une classe d'équivalence, vu qu'on parle de partition. J'ai essayé avec la relation d'équivalence $x\mathcal{R}_Gy \iff f(x)=f(y)$. J'ai vérifié la réflexivité, la symétrie et la transitivité.
Je cherche la classe d'équivalence :$\begin{aligned}Et donc je vais pouvoir écrire :
\bar{x}&=\{y\in G\mid x\mathcal{R}_G y\}\\
&=\{y\in G\mid f(x)=f(y)\}\\
&=\{y\in G\mid f(y)\in\{f(x)\}\}\\
&=f^{-1}(\{f(x)\})
\end{aligned}$
Une réunion non disjointe : $G=\bigcup_{x\in G}\bar{x}=\bigcup_{x\in G}f^{-1}(\{f(x)\})$
Une réunion disjointe : $G=\bigcup_{\bar{x}\in G/\mathcal{R}}\bar{x}=\bigcup_{\bar{x}\in G/\mathcal{R}}f^{-1}(\{f(x)\})$
Mais ça ne m'aide pas pour comprendre le point e).
J'ai également essayé de faire le lien avec l'exercice déjà fait en question (ici). Mais l'application $f$ ici, n'est pas un morphisme. Alors je coince. -
Non, la relation d'équivalence à considérer est $g \mathcal R g' \Leftrightarrow gg'^{-1} \in G_x$, comme dans la question c).
-
Je vois. En fait c'est une autre façon de dire qu'ils sont en relation lorsqu'ils ont même image :$g\mathcal{R}_G g' \iff f(g)=f(g')$
En effet, en l'écrivant, je trouve :
\begin{aligned}
f(g)=f(g')&\iff g.x=g'.x\\
&\iff g^{-1}.(g.x)=g^{-1}.(g'.x)\\
&\iff x=(g^{-1}g').x\\
&\iff g^{-1}g'\in G_x\\
&\iff g'\in gG_x\\
\end{aligned}
D'où je tire que $\bar{g}:=\{g'\in G\mid g\mathcal{R}_Gg'\}=gG_x$.
Par suite, $\large G=\cup_{\bar{g}\in G/\mathcal{R}_G}gG_x$ (union disjointe) et donc $card(G)=\sum_{\bar{g}\in G/\mathcal{R}_G}card(gG_x)$.
Suis-je sur la bonne voie ? -
Oui, il te reste à voir qu'il y a autant d'éléments dans $G/\mathcal R$ que dans $G.x$. Indice : utilise la question c).
-
Bonjour. Je te conseille pour montrer ta formule de considérer l'application $G/G_x\rightarrow G.x$ définie par $\overline{g} \mapsto g.x$, de montrer qu'elle est bien définie et qu'elle est bijective. Le résultat en découlera.
-
Je pense que je viens de comprendre, non sans mal !
Je reprends. Je considère l'application $ \begin{array}{lccl}
f : &G &\rightarrow& G.x \\
&g& \mapsto &g.x
\end{array}$.
Je considère ensuite $\mathcal{R}_f$ la relation d'équivalence associée à cette application et $G/\mathcal{R}_f$ l'ensemble quotient correspondant.
Le théorème de factorisation pour les applications assure que l'application $f$ se factorise par la surjection canonique $\pi$ en une application $\overline{f}:G/\mathcal{R}_f\to G.x$.
Puisque $f$ est surjective, $\overline{f}$ l'est aussi.
Puisque la relation d'équivalence est telle que $x\mathcal{R}_f y \Rightarrow f(x)=f(y)$ et, surtout, $f(x)=f(y)\Rightarrow x\mathcal{R}_f y$, alors $\overline{f}$ est injective.
Par conséquent, l'application $\overline{f}$ est une bijection ensembliste.
Explictions la relation d'équivalence $\mathcal{R}_f$.
Je remarque $g\mathcal{R}_f h\iff h\in gG_x$.
Ce qui signifie que $\mathcal{R}_f=\mathcal{R}_{G_x}$ où $\mathcal{R}_H$ est la relation d'équivalence dont l'ensemble quotient est l'ensemble des classes à gauche modulo $H$.
Je peux donc écrire $G/\mathcal{R}_f = G/\mathcal{R}_{G_x} = G/G_x$.
Et, par la bijection induite, $card(G/\mathcal{R}_f)=card(G/G_x)=card(G.x)$.
Le théorème de Lagrange permet de conclure. -
Boole et Bill a écrit:Bonjour. Je te conseille pour montrer ta formule de considérer l'application $G/G_x\rightarrow G.x$ définie par $\overline{g} \mapsto g.x$, de montrer qu'elle est bien définie et qu'elle est bijective. Le résultat en découlera.
Oui, j'ai vu cette preuve. En fait, je voulais une deuxième corde à mon arc.
D'ailleurs, pour cette application, nommons là $\phi_x$, je prouve qu'elle est bien définie et injective.
Je lis "la surjectivité est évidente", sans autre justification supplémentaire.
Intrigué, j'essaye malgré tout de faire la justification en écrivant la définition :
Soit $y\in G.x$. Ainsi, il existe $g\in G$ tel que $y=g.x$ (par définition de l'orbite $G.x$ de $x$ sous l'action de $G$). Et donc, pour ce $g$ là, on a $\phi_x(\bar{g})=g.x=y$.
C-à-d $\phi_x$ est surjective.
Est-ce cela ? -
Attention, c'est $\phi_x(gG_x) = y$. À part ça c'est bon, je préfère largement cette dernière preuve (même si c'est la même chose que l'autre au fond).
-
Merci ! C'est rectifié.
Pour aller au bout, je pense qu'on peut établir une bijection ensembliste entre $G_x$ et $gG_x$.
Ce qui permet d'écrire :$\begin{aligned}
card(G)&=\sum_{\bar{g}\in G/\mathcal{R}_f}card(gG_x)\\
&=\sum_{\bar{g}\in G/\mathcal{R}_f}card(G_x)\\
&=card(G_x)\sum_{\bar{g}\in G/\mathcal{R}_f}1\\
&=card(G_x)card(G/\mathcal{R}_f)\\
\end{aligned}$
Il reste à montrer que $card(G/\mathcal{R}_f)=card(G.x)$.
C'est-à-dire que les ensembles $G/\mathcal{R}_f:=\{\overline{g}\mid g\in G\}$ et $G.x=\{g.x\mid g\in G\}$ ont même cardinaux.
Je manque de méthode pour le faire. -
Bah c'est la bijection $\phi_x$ qui est la clé ! Sinon c'est la question d) de ton exercice.
-
J'ai montré en d) que $g\in f^{-1}(\{y\})\iff g\in\gamma G_x$ où $y=\gamma.x$ et $\gamma\in G$.
Cela signifie que $\{g\in G\mid g\in f^{-1}(\{y\})\}=\{g\in G\mid g\in\gamma G_x\}$.
D'une part :
$\begin{aligned}
\{g\in G\mid g\in f^{-1}(\{y\})\}&=\{g\in G\mid f(g)=f(\gamma)\}\\
&=\{g\in G\mid \gamma\mathcal{R}_f g\}\\
&=\{\gamma\in G\mid g\mathcal{R}_f\gamma\}\\
&=\bar{g}
\end{aligned}$
D'autre part :
$\begin{aligned}
\{g\in G\mid g\in\gamma G_x\}&=\{g\in G\mid \gamma^{-1}g\in G_x\}\\
&=\{g\in G\mid (\gamma^{-1}g).x=x\}\\
&=\{g\in G\mid g.x=\gamma.x\}\\
&=\{y\in G.x\mid y=g.x\}\\
&=\{g.x\mid g\in G\}\\
&=G.x\\
\end{aligned}$
Donc j'obtiens $\bar{g}=G.x$.
J'ai l'impression d'avoir déraillé quelque part !
Je veux une égalité des cardinaux des ensembles suivants :
$G/\mathcal{R}_f:=\{\overline{g}\mid g\in G\}$ et $G.x=\{g.x\mid g\in G\}$ -
Tu as déraillé puisque $G.x \subset X$ et $\{g \in G \mid g \in \gamma G_x\} \subset G$...
Ça ne te suffit pas de dire que $\phi_x : gG_x \mapsto g.x$ est une bijection de $G/\mathcal R \longrightarrow G.x$ ? -
Si ! Mais je pensais qu'on pouvait prendre le problème par un autre bout encore vu qu'on parle d'image réciproque au départ
-
Bonjour,
j'ai une question autour des classes d'équivalence pour l'application suivante :$\begin{array}{ccccc}
f & : & \mathbb{Z}/p\mathbb{Z} & \to & \mathbb{Z}/p\mathbb{Z} \\
& & \overline{x} & \mapsto & \overline{x}^2 \\
\end{array}$
où $p$ est un nombre premier plus grand que 3.
Pour simplifier, je vais noter $x$ à la place de $\overline{x}$ et $E$ à la place de $\mathbb{Z}/p\mathbb{Z}$. L'application s'écrit donc :$\begin{array}{ccccc}
f & : & E & \to & E \\
& & x & \mapsto & x^2 \\
\end{array}$
Sa relation d'équivalence associée est $x\mathcal{R}_f y\iff f(x)=f(y)$.
Je cherche la classe d'équivalence de $x\in E$ :
Si $x=0$, alors $cl(0)=\{y\in E\mid 0\mathcal{R}_f y\}=\{y\in E\mid y^2=0\}=\{0\}$
Si $x\neq 0$, alors :
$\begin{aligned}
cl(x)&=\{y\in E\mid x\mathcal{R}_f y\}\\
&=\{y\in E\mid y^2=x^2\}\\
&=\{y\in E\mid y=\pm x\}\\
&=\{-x\,,+x\}\\
\end{aligned}$
Je détaille le point suivant :
$\begin{aligned}
y^2=x^2&\iff y^2-x^2=0\\
&\iff (y-x)(y+x)=0\\
&\iff y-x=0\,\,ou\,\, y+x=0\\
&\iff y=x\,\,ou\,\,y=-x\\
\end{aligned}$
Et pour justifier les équivalences j'utilise dans l'ordre le fait que $(\mathbb{Z}/p\mathbb{Z},+,\times)$ soit un anneau puis un corps donc intègre.
Ensuite, par le théorème de factorisation, l'application $f$ se factorise par la surjection canonique $\pi$ en une application $\overline{f}$ au départ de $E/\mathcal{R}_f$ et à valeur dans $E$.
Puisqu'on a l'équivalence $x\mathcal{R}_f y\iff f(x)=f(y)$, alors l'application $\overline{f}$ est injective.
En prenant la corestriction de $f$ à $Im(f)$, on a sa surjectivité donc celle de $\overline{f}$.
Au final, on a une bijection ensembliste entre $E/\mathcal{R}_f$ et $Im(f)$, ce qui permet d'écrire l'égalité :$card(E/\mathcal{R}_f)=card(Im(f))$
J'écris ensuite $E/\mathcal{R}_f=\{cl(x)\,:x\in E\}=\{cl(x)\,:x\in E\setminus\{0\}\}\cup\{0\}=\{\{-x,+x\}\,:x\in E\setminus\{0\}\}\cup\{0\}$.
D'où $card(E/\mathcal{R}_f)=card(\{\{-x,+x\}\,:x\in E\setminus\{0\}\})+card(\{0\})=\frac{p-1}{2}+1=\frac{p+1}{2}$.
Et donc $card(Im(f))=\frac{p+1}{2}$.
En conclusion, puisque $Im(f)=\{f(x)\,:x\in E\}=\{x^2\,:x\in E\}$, ou plus précisément $\{\overline{x}^2\,:\overline{x}\in\mathbb{Z}/p\mathbb{Z}\}$, je déduis qu'il y a dans $\mathbb{Z}/p\mathbb{Z}$ $\frac{p+1}{2}$ carrés.
Est-ce que mon raisonnement est bon ? -
Oui c'est bon. (tu)
PS. Sauf la phrase "Et pour justifier les équivalences j'utilise dans l'ordre le fait que $(\mathbb{Z},+,\times)$ soit un anneau puis un corps donc intègre.".
$(\mathbb{Z},+,\times)$ est un anneau intègre pas un corps. C'est $\mathbb{Z}/p\mathbb{Z}$ qui est un corps. -
Oui, en remarquant bien que -x et x sont différents car p est différent de 2.
-
C'est rectifié !
Oui, j'ai bien noté que $p\ge 3$. On a besoin de cette hypothèse car sinon, on peut travailler dans l'ensemble $\mathbb{Z}/2\mathbb{Z}=\{\overline{0},\overline{1}\}$. Dans ce cas :
- pour $x=0$, $x^2=0$
- pour $x=1$, $x^2=1$
Donc $y^2=x^2$ ssi $x=y$. Je ne sais pas si c'est correctement justifié, mais j'ai saisi l'idée.
Ce qui m'étonne dans cet exercice c'est qu'on écrit $E/\mathcal{R}_f$ ce qui signifie :$\large\mathbb{Z}/_{p\mathbb{Z}/_{\mathcal{R}_f}}$,soit le quotient d'un quotient. Par cette "opération", on a un ensemble que l'on partitionne une première fois. Puis, dans un second temps, on partitionne chaque sous-ensemble obtenu ! C'est la première fois dans un exercice où je vois cela. -
Je viens d'en faire un autre aujourd'hui.
Je suis en train de réaliser que, du fait que $x\mathcal{R}_fy \iff f(x)=f(y)$ soit une relation d'équivalence, on retrouve vraiment très souvent les classes d'équivalence !
Voici l'exercice :
Soit $f$ une bijection involutive sur un ensemble fini $E$. Montrer que si $E$ est de cardinal impair, alors $f$ admet au moins un point fixe.
J'introduis donc la relation d'équivalence sus-cité.
Pour cette relation d'équivalence, je cherches les classes d'équivalence :
$\begin{aligned}
Cl(x)&=\{y\in E\mid x\mathcal{R}_f y\}\\
&=\{y\in E\mid f(y)=f(x)\}\\
\end{aligned}$
Cas 1 : si $y\in Fix(f)$
Dans ce cas, on obtient $f(y)=y$.
Donc, d'une part $f(f(y))=f(y)$ et donc $y=f(y)=f(x)$.
D'autre part : $f(y)=f(x)\iff f(f(y))=f(f(x))\iff y=x$.
Ainsi, $y=x=f(x)$.
Cas 2 : si $y\not\in Fix(f)$
Dans ce cas, on a $f(y)\neq y$.
Donc, d'une part $f(f(y))\neq f(y)$ et donc $y\neq f(y)=f(x)$.
D'autre part : $f(y)=f(x)\iff f(f(y))=f(f(x))\iff y=x$.
Ainsi, $y=x\neq f(x)$.
Pas conséquent :
$Cl(x)=\{y\in E\mid y=x\,\,ou\,\,y=f(x)\}$
Dès lors :
- si $x\in Fix(f)$ alors $f(x)=x$ et donc $Cl(x)=\{x\}$
- si $x\not\in Fix(f)$ alors $Cl(x)=\{x,f(x)\}$
J'en déduis :
$E/\mathcal{R}_f=\{Cl(x)\mid x\in E\}=\{Cl(x)\mid x\in Fix(f)\}\cup\{Cl(x)\mid x\not\in Fix(f)\}=\{\{x\}\mid x\in Fix(f)\}\cup\{\{x,f(x)\}\mid x\not\in Fix(f)\}:=F\cup G$
Puis que :
$\begin{aligned}
card(E)&=\sum_{cl(x)\in E/\mathcal{R}_f}card(cl(x))\\
&=\sum_{cl(x)\in F}card(cl(x))+\sum_{cl(x)\in G}card(cl(x))\\
&=\sum_{cl(x)\in F}1+\sum_{cl(x)\in G}2\\
&=card(F)+2card(G)\\
&\equiv card(F)[2]\end{aligned}$
Donc si $E$ est de cardinal impair, alors $card(E)\equiv 1[2]$ et comme $card(F)\equiv card(E)[2]$ alors, par transitivité, $card(F)\equiv 1[2]$.
Donc, nécessairement, $card(F)\ge 1$ : toute involution bijective sur un ensemble de cardinal impair possède un point fixe.
Qu'en pensez-vous ?
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres
