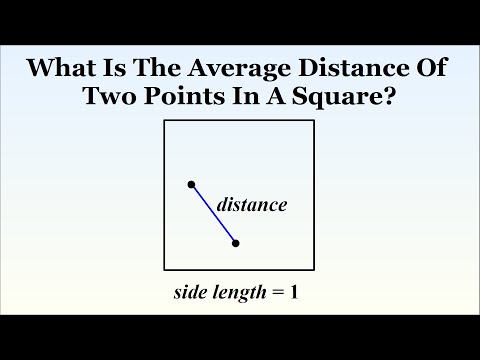
distance moyenne dans un carré

Bonjour,

Je trouve
$$\frac{2+\sqrt{2}}{15} + \frac{1}{3} \ln (1+\sqrt{2}) \simeq 0,5214\;,$$
mais pas en calculant directement l'intégrale d'egoroff-jacquot, que je trouve trop difficile pour moi.

Cordialement,

MC

Bonjour Jacquot,

Je vois que tu habites à Eguisheim. On est presque pays, une partie de ma famille est originaire de Colmar, et j'ai passé une grande partie de mes vacances de jeunesse au fond de la vallée de Munster, à Mittlach. Ca fait un bail que je ne suis pas retourné dans le coin!

Pour ce qui est de la méthode que j'emploie, je ferai un petit topo dessus dans l'après-midi. Mais j'aimerais bien voir le calcul facile d'egoroff.

Cordialement,

MC

Re,

J'utilise pour calculer l'intégrale qui donne la distance moyenne de deux points pris au hasard dans le carré des techniques de géométrie intégrale. Précisément, j'utilise la formule de Cauchy-Crofton qui calcule la longueur d'une courbe plane comme intégrale sur l'espace des droites affines du nombre de points d'intersection d'une droite avec cette courbe. Je précise : notons $D_{\theta,\rho}$ (avec $\theta\in [_\pi/2, \pi/2[$ et $\rho\in \mathbb{R}$) la droite d'équation $x\,\cos\theta +y\,\sin\theta = \rho$ dans un repère orthonormé fixé du plan. Alors, si $\mathcal{C}$ est une courbe rectifiable, sa longueur est donnée par : $$
\int_{-\pi/2}^{\pi/2} \int_\mathbb{R} \frac{1}{2}\,\mathrm{card}(\mathcal{C}\cap D_{\rho,\theta})\,d\rho\,d\theta\;.
$$ On peut voir là http://merganser.math.gvsu.edu/david/reed03/projects/weyhaupt/project.html une page sur la formule de Cauchy-Crofton.
Il est instructif d'appliquer cette formule pour $\mathcal{C}$ un cercle de rayon $R$, ou un segment de longueur $\ell$, pour voir qu'on retrouve bien ce qu'on attend.

La tactique est de remplacer dans l'intégrale qui nous intéresse (écrite par egoroff et jacquot) la longueur du segment par la formule de Cauchy-Crofton : $$
\int_{[0,1]^2}\int_{[0,1]^2}\int_{-\pi/2}^{\pi/2} \int_\mathbb{R} \frac{1}{2} \, \mathrm{card}([p,q]\cap D_{\rho,\theta})\,d\rho\,d\theta\,d\mu(p)\,d\mu(q)\;,
$$ où $\mu$ est la mesure de Lebesgue. Selon la célèbre devise shadok, pourquoi faire simple quand on peut faire compliqué ?

On voit l'intérêt de la manip quand on réécrit l'intégrale $$
\int_{-\pi/2}^{\pi/2} \int_\mathbb{R} \phi(\theta,\rho)\,d\rho\,d\theta\;,
$$ avec $$
\phi(\theta,\rho)=\int_{[0,1]^2}\int_{[0,1]^2} \frac{1}{2} \, \mathrm{card}([p,q]\cap D_{\rho,\theta})\,d\mu(p)\,d\mu(q)\;.
$$ Cette quantité $\phi(\theta,\rho)$ n'est pas trop difficile à calculer géométriquement, car $[p,q]$ rencontre $D_{\rho,\theta}$ quand les deux points $p$ et $q$ sont de part et d'autre de la droite $D_{\rho,\theta}$. Donc $\phi(\theta,\rho)$ vaut le produit des aires des deux morceaux en lesquels la droite $D_{\rho,\theta}$ divise le carré $[0,1]^2$.

Ces aires se calculent facilement en fonction de $\rho$ et $\theta$; on a avantage à distinguer le cas où la droite coupe deux côtés adjacents du carré et celui où elle coupe deux côtés opposés (quand elle ne coupe pas l'intérieur du carré, on a bien sûr 0).

Une fois cette voie tracée, il suffit de suivre l'âne qui trotte.

Maintenant, comme le résultat final n'est pas si affreux que ça, il y a peut-être une voie moins détournée ?

Cordialement,
MC

Salut,

Pour le premier exo d'Eric je dirais avec mon petit dessin $M=1/3$, $4/9$ et la médiane $m=\frac{2-\sqrt{2}}{2}$. J'ai bon ? Je vais réfléchir aux suivants, ils ont l'air très intéressants.

En ce qui concerne l'intégrale de jacquot, j'avais griffoné un début de solution qui me paraissait aboutissable mais je me suis peut-être avancé un peu. Mon idée était de procéder au changement de variable $s=x'+x$, $u=x'-x$, $v=y'+y$, $w=y'-y$ ; on intègre alors $\sqrt{u^2+w^2}$ sur un domaine qu'on peut décrire par $u,w \in [-1,1]$ et $s \in [|u|,2-|u|]$, $v \in [|w|,2-|w|]$ avec un jacobien égal à 4. Au final, grâce à des considérations de parité on obtient l'intégrale double : $$4 \int_{u,w \in [0,1]} (1-u)(1-w) \sqrt{u^2+w^2} \, du \, dw$$ C'est là que les ennuis commencent : j'ai voulu d'abord intégrer en $w$, en faisant le changement $w=u\theta$, j'obtiens $$4\int_{u=0}^1 u^2(1-u) \int_{\theta=0}^{1/u} (1-u \theta) \sqrt{1+\theta^2} \, d\theta \, du$$ Et là j'imagine qu'une IPP peut nous sortir de l'embarras, mais mes réflexes taupinaux m'ont abandonné depuis bien longtemps. Ou alors on pourrait passer en polaire dans l'intégrale précédente mais la forme du domaine n'est pas très encourageante.

PS : mon "fastoche" initial était quand même au moins semi-humoristique, même si je pensais que le calcul était moins difficile.

Bon, une idée peut-être. On écrit $$4\int_{u=0}^1 u^2(1-u) \int_{\theta=0}^{1/u} (1-u \theta) \sqrt{1+\theta^2} \, d\theta \, du=4 \int_{0}^1 u^2(1-u)J(u) \, du$$ où bien sûr $$J(u)=\int_0^{1/u} (1-u \theta) \sqrt{1+\theta^2} \, d\theta$$ On applique la formule de Leibniz-Aleg pour dériver $J(u)$ par rapport à $u$, en remarquant que la borne inférieure ne dépend pas de $u$ et que l'intégrande s'annule à la borne supérieure on obtient comme par magie le résultat que donnerait une "bête" dérivation sous le signe somme sur un intervalle fixe :
$$J'(u)=-\int_0^{1/u} \theta \sqrt{1+\theta^2} \, d\theta=-F(1/u)$$ Or $F$ se calcule explicitement, et sauf erreur $$F(x)=\frac{1}{3} \left( (1+x^2)^{3/2}-1 \right)$$ Je ne pense pas qu'on puisse primitiver facilement $J'(u)=-F(1/u)$ mais une IPP dans l'intégrale initiale, en dérivant $J(u)$ et en primitivant $u^2(1-u)$ permet sans doute de conclure. A suivre.

Bonsoir,

j'essaye de calculer cette espérance, en utilisant le résultat obtenu sur un segment. Mais je crois que j'ai comme un problème, à savoir : les directions des segments sont elles équi-distribuées?

Pour tout dire j'ai pas bien compris la technique de Michel Coste, est-ce que c'est encore jouable pour le cube?

S

Bonsoir,

je ne joue pas dans la même catégorie que vous, et il me faudra du temps pour lire et comprendre la méthode de Michel.

Je pense cependant savoir répondre à la question de samok:
il me semble que toutes les directions ne sont pas équidistribuées because les diagonales du carré sont plus longues que ses médianes, non?

Ce sujet m'a rappelé le problème du spaghetto qui avait suscité une longue discussion sur ce forum l'année dernière

Bonjour,

A propos de l'exercice extrait du livre de Makarov par Eric:

"On choisit au hasard deux points sur la sphère $ S^{n-1}$. Soit $ L_{n}$ la valeur moyenne de la distance les séparant. Prouver que $\lim\limits_{n\to+\infty}L_{n}=\sqrt{2}$"

on peut remarquer qu'en fait la probabilité pour que la distance entre les deux points diffère de $\sqrt{2}$ de plus d'un $\varepsilon >0$ fixé tend vers $0$ quand $n$ tend vers l'infini. On a ici un phénomène de concentration (les probabilistes seraient plus à l'aise pour en parler que moi).

En fait la portion du volume de la $n$-sphère unité représentée par une calotte sphérique de rayon $\dfrac{\pi}{2}-\varepsilon$ (c.-à-d. presque un hémisphère, à $\varepsilon$ près) tend vers 0 quand $n$ tend vers l'infini. De manière imagée, presque tout le monde est à l'équateur à $\varepsilon$ près. La limite $\sqrt{2}$ de l'exercice découle facilement de ce fait.

Un phénomène du même genre se produit pour les boules : la portion du volume de la $n$-boule unité représentée par une boule de même centre de rayon $1-\varepsilon$
tend vers 0 quand $n$ tend vers l'infini. Presque tout le monde est au bord à $\varepsilon$ près. Dans ce cas c'est très facile à voir puisque le rapport des volumes est $(1-\varepsilon)^n$.

On en déduit que la distance moyenne de deux points $x$ et $y$ au hasard dans la $n$-boule unité tend aussi vers $\sqrt{2}$ quand $n$ tend vers l'infini. Et mieux, on a la propriété de concentration suivante : pour $\varepsilon>0$ fixé, la probabilité pour que $1-\Vert x\Vert <\varepsilon$, $1-\Vert y\Vert <\varepsilon$ et $|\Vert y-x\Vert -\sqrt{2}|<\varepsilon$ tend vers 1 quand $n$ tend vers l'infini.

Cordialement,

MC

Bonjour à tous.

Dans ma tentative (désespérée ?) de réhabiliter les intégrales multiples, je voudrais essayer de calculer directement (ou presque) l'intégrale de Jacquot-Egoroff:
\[\int_0^1 \int_0^1 \int_0^1 \int_0^1 \sqrt {(x'-x)^2+(y'-y)^2} \,\textrm dy' \,\textrm dx'\,\textrm dy\,\textrm dx\]
Egoroff ayant refusé le parrainage de cette intégrale, j'ai proposé dans un autre fil de la rebaptiser intégrale de Colmar.
Pour se chauffer je propose de calculer:
\
avec $D=\{x^2 + y^2 \leqslant 1\} = D'=\{x'^2 + y'^2 \leqslant 1\}$.
Pour cela je considère
\[I(x,y) = \iint_{D'} \sqrt {(x'-x)^2+(y'-y)^2} \,\textrm dy' \,\textrm dx'.\]
$I$ est une fonction radiale, $I = f(r)$. Le calcul du laplacien de $I$ donne $f"(r) = 0$.

e.v.

Chapiteau !

Du coup si je ne m'abuse, on trouve $I=4 \pi^2/3$ (j'ai fait le plus gros du boulot). En renormalisant par $\pi^2$, c'est-à-dire ce qu'il faut pour interpréter cette intégrale comme une espérance, on trouve que la distance moyenne entre deux points choisis uniformément dans le disque unité est $4/3$.

Bonjour,

Tiens, plus personne?

Je maintiens ma proposition de $\displaystyle\frac{128}{45\,\pi}\approx 0,905$ pour la distance moyenne de deux points dans le disque unité. Elle tient la route par rapport à une petite simulation.

Je conteste le fait que l'intégrale de ev, qu'on peut écrire
\[ f(r)=\int_0^{2\pi}\!\!\!\int_0^1\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\theta}\;r'\,dr'\,d\theta\;,\]
soit une fonction affine de $r$. Vous pouvez d'ailleurs dériver deux fois $f(r)$ par rapport à $r$, et vous trouverez une quantité visiblement strictement positive.

Cordialement.

Effectivement Ga ?, il y un os dans le boudin. Comme je l'avais fait remarquer dans un autre fil, ça ne marche pas à l'intérieur du disque à causes d'intégrales malpropres.
Y a quequ'chose qui cloche là d'dans...

Il suffit de calculer f(1). pas trop dûr.

e.v. (en vitesse)

Bonjour Ga ?

Je dérive
$ f(r)=\int_0^{2\pi}\!\!\!\int_0^1\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\vartheta}\;r'\,dr'\,d\vartheta\;$,
\begin{align*}
f(r)&=\int_0^{2\pi}\!\!\!\int_0^1\dfrac{(r-r'\cos\vartheta)r'\,dr'\,d\vartheta }{\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\vartheta}}\;\\
f"(r)&=\int_0^{2\pi}\!\!\!\int_0^1\dfrac{r'\,dr'\,d\vartheta }{\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\vartheta}} - \int_0^{2\pi}\!\!\!\int_0^1\dfrac{(r-r'\cos\vartheta)^2 r'\,dr'\,d\vartheta }{\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\vartheta}^3}\;\\
&= \int_0^{2\pi}\!\!\!\int_0^1\dfrac{[r^2+ r'^2-2\,r\,r'\,\cos\vartheta-(r-r'\cos\vartheta)^2] r'\,dr'\,d\vartheta }{\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\vartheta}^3}\;\\
&= \int_0^{2\pi}\!\!\!\int_0^1\dfrac{r'^2(1-\cos^2\vartheta)r'\,dr'\,d\vartheta }{\sqrt{r^2+ r'^2-2\,r\,r'\,\cos\vartheta}^3}\;\\
\end{align*}
expression qui est bien positive, et donc $f"(r) > 0$ même pour $r>1$ contrairement à ce que je croyais. Mes vacances près de Colmar ne m'ont pas apporté la lumière loin de là !

Je ne comprends pas où j'ai fait mes erreurs.

amicalement,

e.v.

Bonjour Ga ?

ev a écrit:

En attendant que ev sauve les intégrales multiples

Ne retiens pas ton souffle ! (j'ai besoin d'idées neuves...)
En attendant (longtemps ?) j'ai plaisir à te lire.

e.v.

Bon je débarque comme un cheveu sur la soupe mais il me semble que l'intégrale en question est quadruple plutôt que sextuple non ? En même temps il se peut que je dise des sottises, je suis encore tout ensommeillé...8-)

Bonjour,

Je vous propose ici de calculer vous même la distance moyenne de deux points dans la boule unité $B$. Le calcul est en fait plus simple que pour le disque. Il s'agit de calculer l'intégrale $$
M= \dfrac{1}{\left(\frac{4}{3}\,\pi\right)^2}\int_B\int_B\ell([p,q])\,d\mu(p)\,d\mu(q)
$$ où $\ell([p,q]$ est la longueur du segment $[p,q]$ et $\mu$ la mesure usuelle sur $\mathbb{R}^3$.

On commence par établir une formule de Cauchy-Crofton pour calculer la longueur d'une courbe rectifiable $C$ dans l'espace. Cette fois-ci, on compte le nombre d'intersections de $C$ avec un plan. Soit $P(u,\rho)$ le plan d'équation $u\cdot x=\rho$ où $u=(u_1,u_2,u_3)$ appartient à l'hémisphère nord $S^2_+$ de la sphère unité (on ne garde que les $u$ avec $u_3\geq 0$) et $\rho\in \mathbb{R}$. On paramètre ainsi les plans affines de $\mathbb{R}^3$ par $S^2_+\times \mathbb{R}$ où on identifie, pour $u$ sur l'équateur, $(u,\rho)$ à $(-u,-\rho)$. On a sur cet espace la mesure $d\mu_{S^2}(u)\,d\rho$ (où $\mu_{S^2}$ est la mesure usuelle sur $S^2$), qui est invariante par l'action des déplacements de l'espace. Les mêmes arguments que ceux employés pour la formule de Cauchy-Crofton dans le plan montrent qu'il existe une constante $k$ telle que
$$\ell(C) = k\, \int_{S^2_+}\int_{\mathbb{R}} \sharp(C\cap P(u,\rho))\,d\rho\,d\mu_{S^2}\;.$$

1) Calculez $k$ en prenant par exemple pour $C$ le segment qui joint l'origine au point $(0,0,1)$.

Pour $|\rho|<1$, le plan $P(u,\rho)$ coupe la boule $B$ en deux morceaux $B_{<\rho}$ et $B_{>\rho}$.

2) Calculez $\varphi(\rho) = \mu(B_{<\rho})\times \mu(B_{>\rho})$.

3) Montrez que $M=\displaystyle \frac{9\,k}{4\,\pi}\, \int_{-1}^1 \varphi(\rho)\,d\rho$,

4) et concluez $M = {?}$.

Cordialement.

Bonsoir,

Je rappelle la solution pour la distance moyenne dans un carré, donnée il y a déjà pas mal de temps :
$$\displaystyle \frac{2+\sqrt{2}}{15} + \frac{1}{3} \ln (1+\sqrt{2}) \simeq 0,5214\;.$$
Il n'y a pas de $\pi$ dedans.

Cordialement.

Bonjour à tous.

Si quelque bonne âme pouvait me dépanner des articles suivants:

SIAM Review 18 (1976) pp. 498-499
American Math Monthly: problem E 2629 [1977,57] et [1978,277].

Merci d'avance.

Trois ans plus tard, les mêmes.

Voici une rédaction du calcul de la distance moyenne de deux points d'un carré de côté 1. Bien sûr, sans chercher à pinailler, il est bien clair que ces points suivent des lois uniformes indépendantes. Soient $(X_{1},Y_{1})$, et $(X_{2}, Y_{2})$, les coordonnées de ces deux points, qui sont des variables aléatoires indépendantes suivant chacune la loi uniforme $\mathcal{U}([0,1])$.
La variable aléatoire $X=\left| X_{1}-X_{2}\right| $ admet la densité $f_{X}(x)=2(1-x)$ sur $[0,1]$. Il en est bien sûr de même pour $Y=\left| Y_{1}-Y_{2}\right| $. Le nombre demandé est l'espérance de $Z=\sqrt{X^{2}+Y^{2}}$, et comme les variav=bles aléatoires $X$ et $Y$ sont indépendantes, on a la formule de transfert : $E(Z)=E(\sqrt{X^{2}+Y^{2}})=\iint_{D}\sqrt{x^{2}+y^{2}}f_{X}(x)f_{Y}(y)dxdy$=$=\iint_{D}4(1-x)(1-y)\sqrt{x^{2}+y^{2}}dxdy$, où $D=[0,1]\times [0,1]$.
Pour raison de symétrie, on a :
$E(Z)=2\iint_{D_{1}}\sqrt{x^{2}+y^{2}}f_{X}(x)f_{Y}(y)dxdy$
$=8\iint_{D_{1}}(1-x)(1-y)\sqrt{x^{2}+y^{2}}dxdy$, où $D_{1}=\{(x,y)\in \R^{2}/0\leq y\leq x\leq 1\}$.
On calcule cette dernière intégrale en passant en polaires. C'est un peu long, mais ça se fait, et c'est du niveau, mettons de BCPST2.
On peut chercher aussi la variance. C'est un exemple d'une situation où le moment d'ordre 2 est plus simple à calculer que l'espérance. On avait posé ceci dans "Le Nouvel Archimède" n° 7, janvier 1986.
Il paraît qu'on y arrive aussi avec un cube ... Et après ... ?
Bonne soirée.
RC

Intéressant, ce vieux fil...

Il me semble que c'est traité dans le fil, plus haut. Et qu'il en est question aussi dans une RMS récente. Mais ça a l'air diablement compliqué.