Cercle tangent à trois cercles 2 à 2 tangents
Bonjour,
Soient $C_1$, $C_2$ et $C_3$ trois cercles deux-à-deux tangents comme les trois gros cercles de la figure de gauche. Dans ce cas, je sais comment avoir le cercle intérieur tangent à $C_1$, $C_2$ et $C_3$ (le petit cercle sur la figure). C'est ce qu'on appelle le cercle intérieur de Soddy, et on trouve les formules sur le ouebbe.
Maintenant soit $C_4$ le cercle extérieur tangent à $C_1$, $C_2$ et $C_3$, le gros cercle sur la figure de droite. C'est le cercle extérieur de Soddy. Je ne sais pas comment avoir le cercle tangent à $C_1$, $C_2$ et $C_4$ autre que $C_3$. Sauriez-vous ?
Soient $C_1$, $C_2$ et $C_3$ trois cercles deux-à-deux tangents comme les trois gros cercles de la figure de gauche. Dans ce cas, je sais comment avoir le cercle intérieur tangent à $C_1$, $C_2$ et $C_3$ (le petit cercle sur la figure). C'est ce qu'on appelle le cercle intérieur de Soddy, et on trouve les formules sur le ouebbe.
Maintenant soit $C_4$ le cercle extérieur tangent à $C_1$, $C_2$ et $C_3$, le gros cercle sur la figure de droite. C'est le cercle extérieur de Soddy. Je ne sais pas comment avoir le cercle tangent à $C_1$, $C_2$ et $C_4$ autre que $C_3$. Sauriez-vous ?
Réponses
-
-
Avec le théorème de Descartes, tu peux trouver le rayon du cercle, et avec la version complexe du théorème, tu peux trouver le centre. Cf https://fr.wikipedia.org/wiki/Théorème_de_Descartes
-
Ah non, les rayons sont bons. J'avais oublié le signe négatif de la courbure du cercle extérieur. Je bosse les centres maintenant...
-
C'est bon je m'en suis sorti. Merci @Guego. Mais les formules de Descartes donnent 4 possibilités. J'ai tranché en regardant le résultat, je ne sais pas comment trancher automatiquement.
-
C'est bon j'ai trouvé. Dans mon cas il n'y a que deux possibilités (je m'en suis rendu compte empiriquement). Pour trancher, il faut prendre le cercle dont le centre est plus éloigné que le centre de l'autre du gros cercle extérieur.
Je peux faire la fractale à présent :-) -
Saturne a eu la politesse de répondre en MP qu'il n'a pas vu la vidéo car il a du mal à se concentrer sur des vidéos.
Une attitude qui est peut-être assez courante chez les lecteurs de ces forums ?
Mais il y a des vidéos de toutes sortes !
Je vais essayer de vendre la mienne :
il y a des textes, des figures avec plus de détails que sur wikipédia, et on peut mettre en pause, couper le son !(:P)
De plus, un programme interactif est associé...
D'autre zolies figures comme celles introduites par Saturne :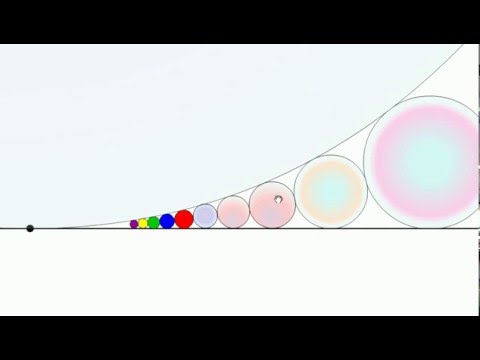
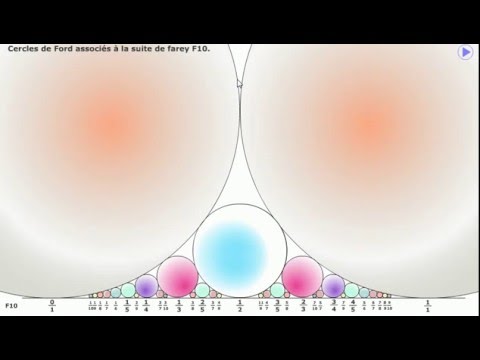
-
Que veux-tu, je suis un nerveux moi, je tiens pas en place ^^
Ok, je vais jeter un oeil à ces vidéos :-) -
Question indiscrète : pour ajouter tous les disques, vous faites une recherche en largeur ou en profondeur ? (Je ne sais pas si c'est une question très pertinente parce qu'il n'y a pas tout à fait un arbre mais bon.)
-
En fait, une exploration « en largeur » (plus intuitive qu'en profondeur) en gardant la trace des cercles produits à chaque « génération » suffit pour épuiser tous les cercles de rayon plus grand qu'un seuil donné. Ci-joint un résultat avec des trous (zones qui devraient être couvertes mais ne le sont pas) vraiment tout petits (voir surtout le pdf).
-
Bonjour @Math Coss,
Je ne comprends pas bien ce que tu as écrit. Tu as un problème avec le dessin ?
Ci-dessous mon code (R) si ça peut aider. J'utilise une fonction récurrente.library(plotrix) # for the draw.circle function # radius of the inner Soddy circle #### soddyRadius <- function(r1,r2,r3){ 1/(1/r1+1/r2+1/r3+2*sqrt(1/r1/r2+1/r2/r3+1/r3/r1)) } # center of the inner Soddy circle (equal detour point) #### soddyCenter <- function(A,B,C){ measure <- function(M,N){ sqrt(c(crossprod(N-M))) } a <- measure(B,C) b <- measure(A,C) c <- measure(A,B) AB <- B-A AC <- C-A Delta <- 0.5*abs(AB[1]*AC[2]-AB[2]*AC[1]) # area of triangle ABC tc <- 1 + 2*Delta/c(a*(b+c-a), b*(c+a-b), c*(a+b-c)) # triangular coordinates den <- c(tcrossprod(t(tc), c(a,b,c))) k1 <- a*tc[1]/den k2 <- b*tc[2]/den k3 <- c*tc[3]/den k1*A + k2*B + k3*C } # case of an exterior circle C3 (using Descartes' theorems) #### soddyCircles <- function(C1, C2, C3){ r1 <- C1$radius; r2 <- C2$radius; r3 <- -C3$radius soddyR <- soddyRadius(r1,r2,r3) z1 <- C1$center[1] + 1i*C1$center[2] z2 <- C2$center[1] + 1i*C2$center[2] z3 <- C3$center[1] + 1i*C3$center[2] term1 <- 1/r1*z1+1/r2*z2+1/r3*z3 term2 <- 2*sqrt(1/r1/r2*z1*z2+1/r2/r3*z2*z3+1/r1/r3*z1*z3) soddyCenter1 <- (term1 - term2)*soddyR soddyCenter2 <- (term1 + term2)*soddyR soddyCenter1 <- c(Re(soddyCenter1), Im(soddyCenter1)) soddyCenter2 <- c(Re(soddyCenter2), Im(soddyCenter2)) sols <- list( list(center=soddyCenter1, radius=soddyR), list(center=soddyCenter2, radius=soddyR) ) d1 <- c(crossprod(soddyCenter1-C3$center)) d2 <- c(crossprod(soddyCenter2-C3$center)) if(d1>d2) sols[[1]] else sols[[2]] } # draw a circle #### drawCircle <- function(C, ...){ draw.circle(C$center[1], C$center[2], C$radius, ...) } # starting circles #### C1 <- list(center=c(1,0),radius=1) C2 <- list(center=c(-1,0),radius=1) C3 <- list(center=c(0,sqrt(3)),radius=1) C4 <- list(center = soddyCenter(C1$center,C2$center,C3$center), radius = 2 + soddyRadius(C1$radius,C2$radius,C3$radius)) # main function (recursive) #### Apollony <- function(C1, C2, C3, n, colors=FALSE, exterior=FALSE, ...){ if(exterior){ Cnew <- soddyCircles(C1,C2,C3) }else{ soddyCenter <- soddyCenter(C1$center,C2$center,C3$center) radius <- soddyRadius(C1$radius,C2$radius,C3$radius) Cnew <- list(center=soddyCenter, radius=radius) } drawCircle(Cnew, col=if(colors) Colors[n] else NA, ...) if(n==1) return(invisible()) Apollony(Cnew,C2,C3,n-1, colors=colors, exterior = exterior) Apollony(C1,Cnew,C3,n-1, colors=colors, exterior = exterior) Apollony(C1,C2,Cnew,n-1, colors=colors) } # Apollony fractal #### par(mar=c(0,0,0,0)) plot(0, 0, type="n", axes=FALSE, xlab=NA, ylab=NA, ylim=c(-1.6,2.74), asp=1) drawCircle(C1); drawCircle(C2); drawCircle(C3); drawCircle(C4) n <- 5 Apollony(C1, C2, C3, n) Apollony(C1, C2, C4, n, exterior=TRUE) Apollony(C1, C3, C4, n, exterior=TRUE) Apollony(C2, C3, C4, n, exterior=TRUE) -
Merci pour le code. J'avais un problème en effet mais je l'ai résolu. Voici ce que je voulais dire.
On peut considérer les cercles comme les sommets d'un graphe dont les arêtes sont les paires de cercles tangents. Disons que l'on appelle « génération $0$ » le grand cercle et le petit cercle central (qui semblent être dans C4), « génération $1$ » les trois cercles de même rayon tangents (C1, C2 et C3). La génération d'un cercle est la distance de ce cercle à l'un de ceux de C4. L'ingrédient principal pour produire de nouveaux cercles, c'est le théorème de Descartes (incarné par la fonction soddyCircles), qui produit un nouveau cercle à partir de trois cercles mutuellement tangents (il devrait y en avoir deux mais l'un des deux est déjà connu).
La question est de savoir comment explorer ce graphe. Apparemment, ce que tu fais, c'est produire de nouveaux cercles sans états d'âme, et ce, cinq fois de suite (n <- 5). Il ne t'a pas échappé que le processus est exponentiel. Chez moi, avec 6 ou 7 générations, il y avait un très grand nombre de cercles dont un bon nombre étaient invisibles (rayon trop petit), c'était très lent pour rien. Je me suis mis à écrémer en n'ajoutant pas les cercles trop petits, de sorte à ne remplir que ce qui est nécessaire.
Le résultat du déroulement, c'est que le nombre de triplets de cercles à traiter à chaque génération augmente vite pour atteindre près de 2000 vers les générations 7-8 pour diminuer jusqu'à zéro quand tous les cercles (de rayon supérieur au seuil fixé, 1/500 sur le pdf ci-dessus) ont été calculés, un peu avant la génération 30.
Après, il y avait la question parcours en largeur parcours en profondeur : un parcours en profondeur serait probablement plus futé en principe mais finalement inutile ici.
PS : nombre de triangles à traiter par génération avec un seuil de 1/1000 :[6, 18, 54, 162, 486, 864, 2052, 2376, 1224, 648, 414, 234, 162, 81, 81, 72, 36, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 0, 0]
-
Ok.
Si ces fractales t'amusent, pour info il y a aussi celle-ci, plus simple (il n'y a pas de cercle extérieur ici). -
Bonjour,
je joins une solution en utilisant l'espace des cercles (orientés) qui est la pseudo-sphère unité de l'espace de Minkowski-Lorentz de dimension 4.
La résolution se fait en deux temps :
- résolution d'un système de trois équations linéaires à trois inconnues et un paramètre ;
- le paramètre est solution d'une équation du second degré.
Cerise sur le gâteau, la même résolution fonctionne si les cercles ne sont pas tangents : on résout le problème d'Apollonius avec un couple solution selon les orientations choisies pour les cercles de départ. On peut aussi remplacer un ou des cercle(s) par une ou des droite(s); la méthode fonctionne encore.
On peut aussi généraliser : on peut remplacer les cercles orientés du plan par des sphères orientées de l'espace et on utilise l'espace des sphères (orientées) qui est la pseudo-sphère unité de l'espace de Minkowski-Lorentz de dimension 5. On obtient comme solution non plus deux points, mais une conique qui représente une cyclide de Dupin.
Lionel
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres



