Réduction triangle quelconque
Bonjour
J'ai besoin de votre aide.
J'ai un triangle quelconque dans un plan cartésien. Je connais les coordonnées de ses 3 points.
Je souhaite réduire ce triangle de manière à ce que l'espace entre les côtés des 2 triangles soit le même.
J'ai essayé de vous faire un dessin.
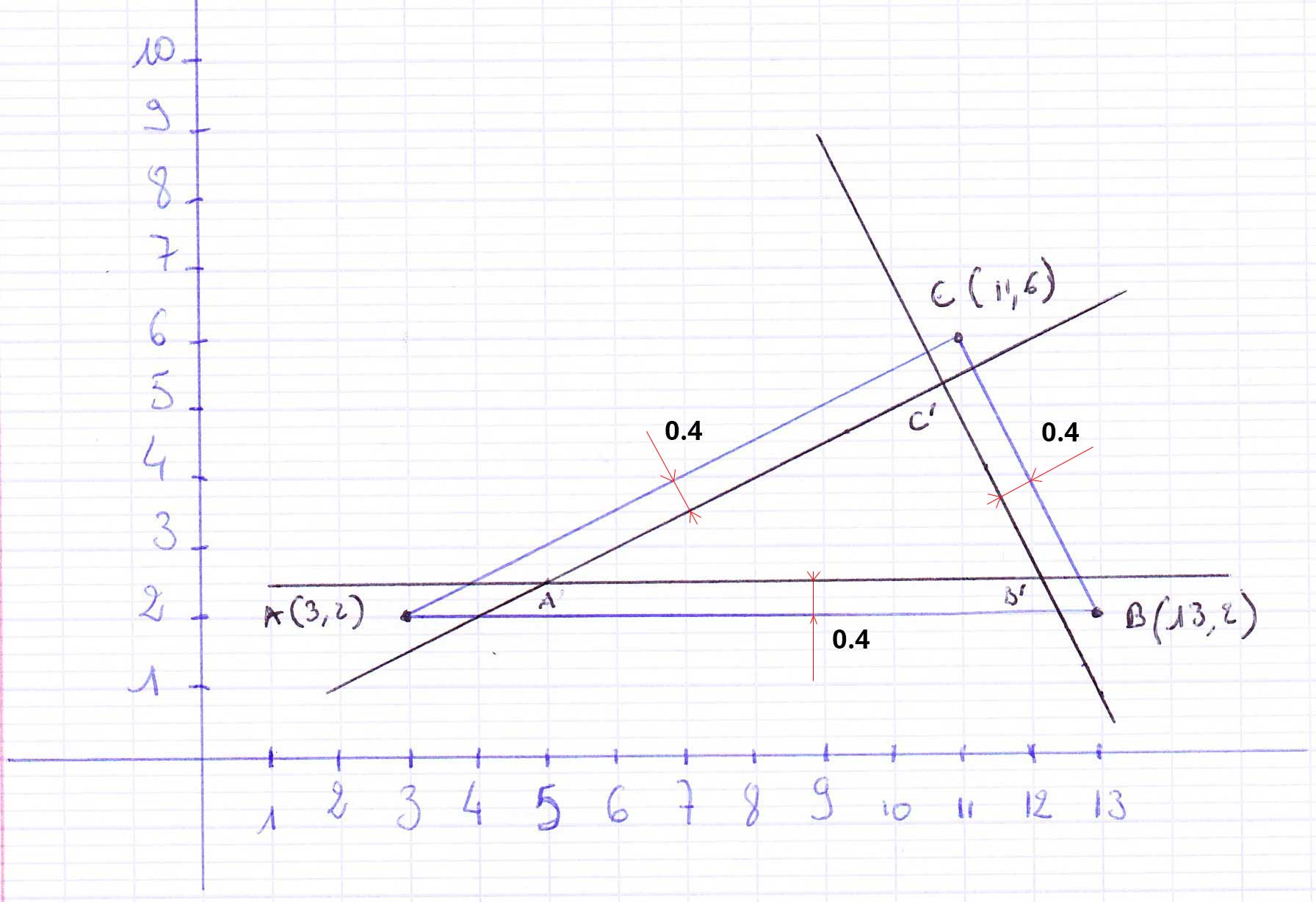
Pourriez-vous m'aider à calculer les coordonnées des 3 points du triangle réduit s'il vous plaît ?
Merci d'avance.
Bien à vous,
Romain
J'ai besoin de votre aide.
J'ai un triangle quelconque dans un plan cartésien. Je connais les coordonnées de ses 3 points.
Je souhaite réduire ce triangle de manière à ce que l'espace entre les côtés des 2 triangles soit le même.
J'ai essayé de vous faire un dessin.

Pourriez-vous m'aider à calculer les coordonnées des 3 points du triangle réduit s'il vous plaît ?
Merci d'avance.
Bien à vous,
Romain
Réponses
-
Une idée qui me vient : puisque l'on est dans un repère, on pourrait déterminer les équations des droites portées par les côtés du triangles puis les équations des droites portées par les côtés du petit triangle.
Sans savoir si c'est judicieux. -
Les nouvelles coordonnées de C' sont
(10.82, 5.46)
au centième près.
Les valeurs exactes sont compliquées.
De retour dans la soirée. -
Oui, je pense que la méthode de Dom est la plus simple.
Sinon, géométriquement parlant, $A',B'$ et $C'$ appartiennent aux bissectrices des angles du triangle $ABC$
On a une homothétie dont le centre est celui du cercle inscrit et le rapport $\dfrac {r-4}r$ où $r $ est son rayon. Mais bonjour les calculs. -
Merci a tous pour vos retours.
Une petite précision, il faut que la solution soit applicable a n'importe quel triangle.
Je suis pas très fort en géométrie, j'ai donc besoin de vous pour trouver les formules nécessaires au calcul des coordonnées des points du triangle réduit. -
Alors c'est parti : $A(x_A;y_A)$, $B(x_B;y_B)$, $C(x_C;y_C)$ non alignés.
Je pars pour un moment (ouf !). -
Voici ce que donne la méthode de jacquot.
Soit $S$ l'aire du triangle, $r$ le rayon du cercle inscrit et $a=BC$, $b=CA$ et $c=AB$.
On calcule $a,b,c$ par $a=\sqrt{(x_B-x_C)^2+(y_B-y_C)^2}$, etc.
On sait que $2S=(a+b+c)r=|x_By_C+x_Cy_A+x_Ay_B-y_Bx_C-y_Cx_A-y_Ax_B|$ donc on calcule $r$ par
$r=\dfrac{|x_By_C+x_Cy_A+x_Ay_B-y_Bx_C-y_Cx_A-y_Ax_B|}{a+b+c}$.
On calcule les coordonnées du point $I$ par $I=\dfrac{aA+bB+cC}{a+b+c}$.
Soit $d=0.4$ (la distance entre le petit et le grand triangle).
On a $A'=\dfrac{dI+(r-d)A}{r}$, etc. -
Pour A' (mettez des flèches partout) :
OA' = OC' +k(2, 1) -
Merci encore.
Encore une petite précision.
Les éléments connus, les dimensions de $AB$, $BC$ et $AC$, les coordonnées des points $A$, $B$ et $C$ et la distance entre le petit et le grand triangle.
@JLT serait-il possible d’expliquer un peu plus s'il vous plait ?
Je ne comprends pas le calcul $I=\dfrac{aA+bB+cC}{a+b+c}$.
À quoi correspond $A$, $B$ et $C$ ?
J'ai besoin des coordonnées de $A'$, $B'$ et $C'$, or je ne vois pas comment les calculer. -
$A$ est le point $(x_A,y_A)$.
$aA$ signifie $(ax_A,ay_A)$.
On a donc $I=\Big(\dfrac{ax_A+bx_B+cx_C}{a+b+c},\dfrac{ay_A+by_B+cy_C}{a+b+c}\Big)$. -
Une alternative : (mais il reste du travail...)
Quitte à translater le triangle et à le (re)tourner un petit peu, je considère que les coordonnées de $A$, $B$ et $C$ sont les suivantes :
$A(0;0)$, $B(x_B;0)$, $C(x_C;y_C)$ où $y_C>0$ (on choisit de placer $C$ dans le demi-plan supérieur).
Quitte à changer le nom des points, je m'arrange pour que $0< x_C <x_B$ (j'exclus pour le moment le cas du triangle rectangle), ainsi, $C$ est au dessus du segment $[AB]$.
On obtient les équations cartésiennes de droites suivantes :
$(AB) : y = 0$
$(AC) : y = \dfrac{y_C}{x_C} x$
$(BC) : y = \dfrac{y_C}{x_C-x_B} x - \dfrac{y_Cx_B}{x_C-x_B} $
Ensuite, des calculs (peut distrayants) permettent de trouver les équations des droites $(A'B')$, $(A'C')$ et $(B'C')$ : j'ai noté $d$ la distance donnée (sans me soucier de son ensemble de définition car ce $d $ ne doit pas être trop grand si l'on veut une réduction.)
$(A'B') : y = d$
$(A'C') : y = \dfrac{y_C}{x_C} x - \dfrac{d\left( \left( \dfrac{y_C}{x_C} \right) ^2 + 1 \right)}{\sqrt{2} \left|\dfrac{y_C}{x_C} \right|}$
$(B'C') : y = \dfrac{y_C}{x_C-x_B} x - \dfrac{y_Cx_B}{x_C-x_B} - \dfrac{d\left( \left( \dfrac{y_C}{x_C-x_B} \right) ^2 + 1 \right)}{\sqrt{2} \left|\dfrac{y_C}{x_C-x_B} \right|} $
S'il n'y a pas d'erreurs 8-), on peut retrouver les coordonnées des points $A'$, $B'$ et $C'$.
A faire...
Puis il faudra retourner à l'envers et translater à l'envers pour retrouver les coordonnées voulues
A faire... -
Houalalala....c'est à la fois rudimentaire et calculatoire...sans aucune ingéniosité...8-)
Première partie : recherche de la distance entre deux droites "générales"
Soient deux droites parallèles dont le coefficient directeur est $a$ réel non nul.
$\mathcal D : y=ax+b$
$\mathcal D' : y=ax+b' $
On note la distance $d$ entre les deux droites.
Je n'ai pas été astucieux : je place un point $M(u, au+b)$ sur $\mathcal D$.
Je considère la droite $\mathcal T$ perpendiculaire à $\mathcal D$ passant par $M$.
Je sais que le produit des coefficients directeurs de deux droites perpendiculaires vaut $-1$.
Je trouve : $\mathcal T : y=-\dfrac{1}{a} x+\left( a +\dfrac{1}{a} \right) u+b$ (à vérifier)
Je note $M'$ le point d'intersection de $\mathcal T$ avec $\mathcal D'$.
Je trouve : $M'\left( \dfrac{a(b-b')}{a^2+1}+u \, ; \, \dfrac{a^2(b-b')}{a^2+1}+au+b \right)$ (à vérifier)
Puis $d=MM'$ donc : $d=\dfrac{\sqrt{2}|a||b-b'|}{a^2+1}\qquad$ (à vérifier)
Remarque : cela reste vrai dans le cas $a=0$ de deux droites "horizontales", mais pas le cas des droites "verticales". -
Deuxième partie : on travaille à l'envers, on donne $\mathcal D : y=ax+b$ et $d$ un réel strictement positif et on cherche l'équation d'une droite (il y en a exactement deux) $\mathcal D' : y=ax+b'$ qui est la distance $d$ de la droite $\mathcal D$.
On étudie le cas $a\neq 0$.
De ce qui précède on déduit : $|b-b'|=\dfrac{d(a^2+1)}{\sqrt{2}|a|}$
Donc : $b'=b \pm \dfrac{d(a^2+1)}{\sqrt{2}|a|}$
Selon que la droite cherchée est au dessus ou en dessous la première, on choisit le signe.
Dans ma configuration, comme sur ton dessin, ces deux droites sont en dessous, d'où le $"-"$.
Tout cela demande à être vérifié.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres
Qui est en ligne 7
7 Invités

