Construction des racines d'un trinôme

Bonjour
Je salue Claude Quitté qui nous fait l'honneur de nous rendre visite.
Je ne connaissais pas le cercle de Carlyle ou plus précisément je ne connaissais pas son géniteur!
Voici la figure de Claude dans toute sa splendeur.
Elle se passe dans $\mathbb R^2$ euclidien usuel.
Le cercle rouge de diamètre $FM$ est le cercle de Carlyle.
Il coupe la droite réelle aux points d'abscisses $x_1$ et $x_2$ racines du polynôme $X^2-sX+p$.
Ces racines sont réelles si et seulement si $M(s,p)$ est à l'extérieur de la parabole noire de foyer $F(0,1)$ et de tangente au sommet la droite réelle.
La figure montre la connexion qui existe entre ces racines et les tangentes issues du point $M$ à la parabole.
Mais ceci n'a plus strictement aucune importance puisque tout ce que l'on doit savoir sur la parabole est son équation réduite.
Amicalement
[small]p[/small]appus
PS
Sur la figure de Claude, on lit la formule $x_1x_2=p$ en évaluant la (défunte) puissance de $O(0,0)$ par rapport au cercle de Carlyle.
On lit aussi la formule $x_1+x_2=s$ en projetant orthogonalement le diamètre $FM$ sur la droite réelle.

Merci à vous tous.

Je vais me coucher moins schtroumpf.

Amicalement,

e.v.

Bonsoir
Sur la figure de Claude, j'ai rajouté en bleu la construction des tangentes issues de $M$ à la parabole telle qu'on pouvait la trouver dans le Lebossé-Hemery.
On passe du bleu au rouge par une défunte homothétie de centre $F$. et de rapport $\dfrac 12$.
Amicalement
[small]p[/small]appus

J'ai utilisé le cercle de Carlyle découvert dans ce fil pour ce programme utilisable au lycée :

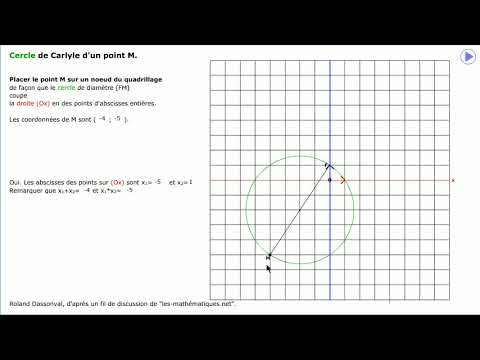
La référence au forum est donnée en lien.
J'espère que les modérateurs n'y verront pas d'inconvénient ; je peux modifier...
Erreur à corriger ? Modifications à apporter ?
Critiques et propositions bienvenues...