Triangle équilatéral inscrit dans parabole
Bonjour,
Étant donnée une parabole (foyer et directrice), comment construire un triangle équilatéral inscrit dans cette parabole ?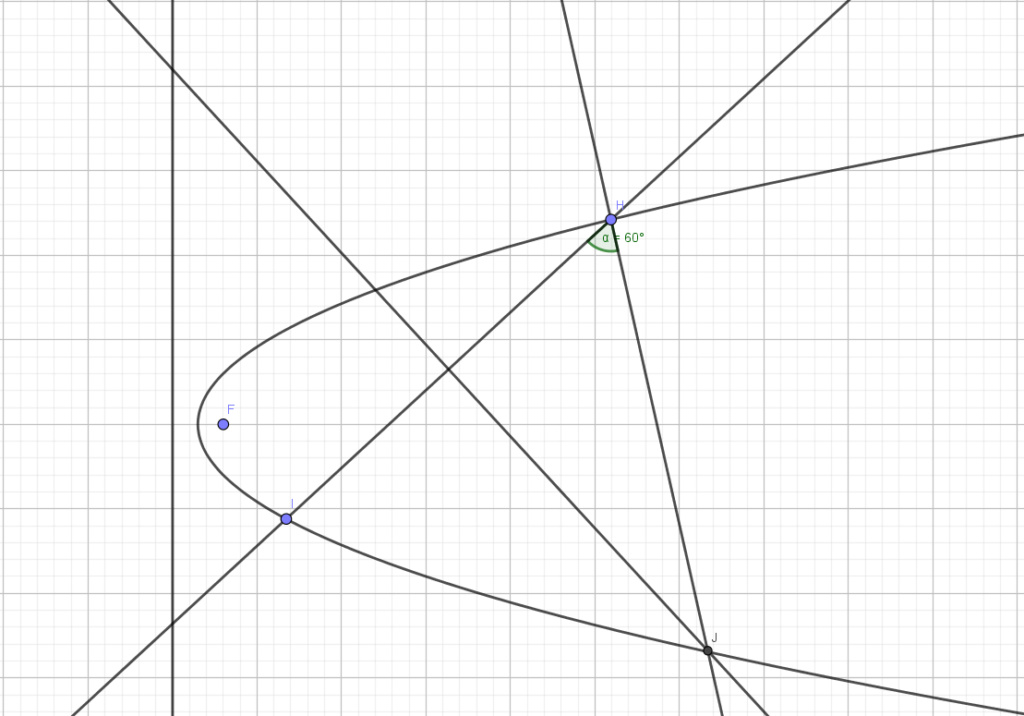
J'ai fixé le point $I$, $H$ est variable. J'ai construit l'angle $\hat{H} = 60°$, puis $J$ se trouvant sur la médiatrice de $[HI]$. En déplaçant $H$, j'arrive à placer $J$ sur la parabole mais la construction n'est pas rigoureuse...
Étant donnée une parabole (foyer et directrice), comment construire un triangle équilatéral inscrit dans cette parabole ?

J'ai fixé le point $I$, $H$ est variable. J'ai construit l'angle $\hat{H} = 60°$, puis $J$ se trouvant sur la médiatrice de $[HI]$. En déplaçant $H$, j'arrive à placer $J$ sur la parabole mais la construction n'est pas rigoureuse...
Réponses
-
Bonjour
On avait du voir quelque part sur le forum, qu'étant un point $M=\left( x,y\right) $ de la parabole d'équation $y^{2}=2px$ (en orthonormé), le cercle centré en $\left( x+4p,-\dfrac{y}{3}\right) $ passant par $M$ recoupe la parabole aux sommets d'un triangle équilatéral et qu'on obtient ainsi tous les triangles équilatéraux inscrits dans la parabole..
Bien cordialement. Poulbot -
Merci beaucoup ! Simple et efficace (tu)
-
Bonjour Mieses
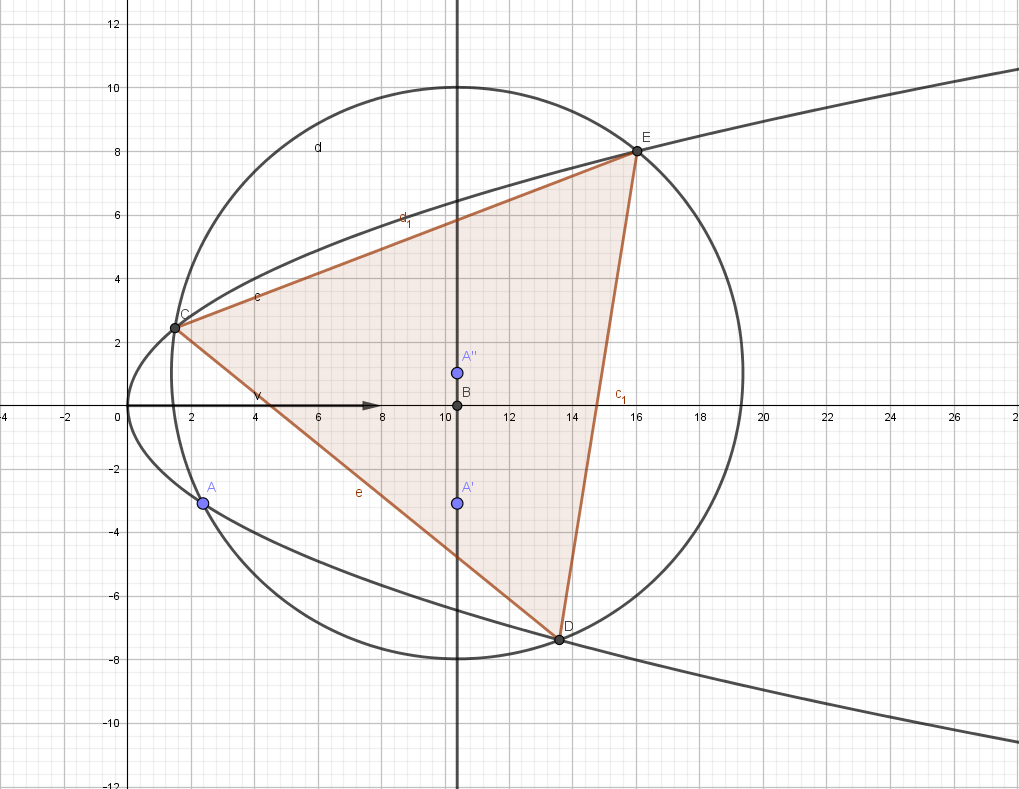
Un problème un peu plus compliqué : étant donné un point $M\left( x,y\right) $ de la parabole $P$ $\left( y^{2}=2px\right) $, construire les triangles équilatéraux de sommet $M$ inscrits dans $P$.
Il y en a entre $1$ et $3$. La figure représente un cas où il y en a $3$.
Ma méthode consiste à trouver leurs centres, ce qui, évidemment, avec leur sommet $M$, permettra de trouver les autres sommets.
La parabole $P^{\prime }$ d'équation $9y^{2}-2px+8p^{2}=0$ est le lieu des centres des triangles équilatéraux inscrits dans $P$.
$H$ est l'hyperbole équilatère de centre $\left( x-\dfrac{2p}{3},\dfrac{y}{3}\right) $, d'asymptotes parallèles aux axes et passant par $M$.
$H$ et $P^{\prime }$ ont au plus $3$ communs; chacun est centre d'un triangle équilatéral de sommet $M$ inscrit dans $P$.
Sauf erreur (probable) de ma part, il y a une $1$, $2$ ou $3$ solutions selon que $x<\lambda ,x=\lambda ,x>\lambda $ où $\lambda =\dfrac{13+16\sqrt{2}}{6}p$.
Bien cordialement. Poulbot -
Un sujet de concours sur les triangles équilatéraux inscrits dans des courbes données (Centrale 91).
Cordialement, j__j -
@ poulbot
Je n'ai pas retrouvé sur le forum les messages qui démontrent la première construction que tu m'as donnée. Mais j'ai trouvé comment faire en suivant la correction d'un exercice dans le livre d'exercices de Bernard Gostiaux Exercices de mathématiques spéciales. Je m'inspire de la méthode développée pour déterminer le lieu des centres des triangles équilatéraux inscrits dans une parabole.
On cherche les conditions pour qu'un cercle coupe la parabole en trois points formant un triangle équilatéral.
Paramétrisation du cercle coupant la parabole
Soit $(a,b)$ les coordonnées d'un point $\Omega$, le cercle de centre $\Omega$ et de rayon $R$ se paramètre par : $$
x = a + R\cos t, \quad y = b + R\sin t .
$$ On pose $u = e^{it}$ on a $ \cos t = \frac{1}{2} \left( u + \frac{1}{u} \right )$, puis $\sin t = -\frac{i}{2} \left( u - \frac{1}{u} \right )$. On obtient la paramétrisation : $$
x = a + \frac{R}{2} \left( u + \frac{1}{u} \right ), \quad y = b -i\frac{R}{2} \left( u - \frac{1}{u} \right ).
$$ Points d'intersection du cercle et de la parabole
Ce sont les solutions de module égal à 1 de l'équation d'inconnue $u$ : $$
\left (b-i\frac{R}{2} \left( u-\frac{1}{u} \right) \right )^2 -2p \left( a+ \frac{R}{2} \left( u+ \frac{1}{u} \right ) \right )= 0.
$$ En développant, on est amené à étudier les racines du polynôme $Q(u)$ avec : $$
Q(u) = \frac{R^2}{4}u^4 + R(p+ib)u^3 + u^2\left(2pa-b^2-\frac{R^2}{2}\right) + uR(p-ib) +\frac{R^2}{4}
$$ On montre que ce polynôme admet 4 racines de module 1 du type $\alpha$, $j\alpha$, $j^2\alpha$, et $\beta$.
$\alpha$, $j\alpha$, $j^2\alpha$ donnent les sommets du triangle équilatéral ; $\beta$ correspond au point de coordonnées $(x_{\beta}, y_{\beta})$ choisi arbitrairement sur la parabole pour commencer la construction.
On a une expression simple de $\beta$ en faisant la somme des racines : $$
\alpha + j\alpha + j^2\alpha + \beta = \beta = -\frac{4}{R}(p+ib)
$$ On en déduit alors $x_{\beta} = a - 4p, \quad y_{\beta} = -3b$, d'où les coordonnées de $\Omega$ : $$
a = x_{\beta} + 4 p, \quad b = -\frac{1}{3}y_{\beta}.
$$ Pour la seconde construction où l'on part d'un des sommets, je sèche car l'expression de $\alpha$ est nettement plus compliquée... Je ne vois pas comment faire apparaître l'hyperbole dont tu parles. -
Bonjour Mieses et merci pour tes explications
"Je ne vois pas comment faire apparaître l'hyperbole dont tu parles."
Je n'ai pas vraiment finassé.
Prenant $M=\left( \dfrac{t^{2}}{2p},t\right) \in P,\Omega =\left( \dfrac{\mu ^{2}}{2p}+4p,-\dfrac{\mu }{3}\right) \in P^{\prime }$, j'ai cherché la condition pour que les $2$ autres sommets du triangle équilatéral de sommet $M$ et de centre $\Omega $ soient sur $P$ et j'ai obtenu $\mu ^{3}+t\mu ^{2}+\left( \dfrac{28}{3}t^{2}-p^{2}\right) \mu +12p^{2}t-t^{3}=0$ $\left( 1\right) $.
La condition pour que l'hyperbole équilatère de centre $\left( \alpha ,\beta \right) $, d'asymptotes parallèles aux axes et passant par $M$ passe aussi par $\Omega $ est $\left( \dfrac{\mu ^{2}}{2p}+4p-\alpha \right) \left( -\dfrac{\mu }{3}-\beta \right) =\left( \dfrac{t^{2}}{2p}-\alpha \right) \left( t-\beta \right) $.
C'est la même que $\left( 1\right) $ si $\left( \alpha ,\beta \right) =\left( \dfrac{t^{2}}{2p}-\dfrac{2p}{3},\dfrac{t}{3}\right) $.
@john_john Merci pour ton énoncé.
Amicalement. Poulbot -
Bonjour Mieses
Je viens de réaliser que l'on peut, plus simplement (voir figure), utiliser un cercle à la place de l'hyperbole $H$ :
si $M=\left( x,y\right) \in P$, on sait que $M^{\prime }=\left( x+4p,-\dfrac{y}{3}\right) \in P^{\prime }$. Le cercle centré en $O=\left( x+\dfrac{16}{9}p,y\right) $ passant par $M^{\prime }$ recoupe $P^{\prime }$ aux centres des triangles équilatéraux de sommet $M$ inscrit dans $P$.
Je suggère de reprendre ces $2$ petits problèmes dans le cas d'une hyperbole équilatère en remarquant que le centre d'un triangle équilatéral inscrit dans une hyperbole équilatère est sur l'hyperbole, vu que c'est l'orthocentre du triangle (merci Poncelet).
Le fait que, si $M$ est sur l'hyperbole, le cercle centré au point $M^{\prime }$ diamétralement opposé à $M$ sur l'hyperbole et passant par $M$ la recoupe aux sommets d'un triangle équilatéral est connu depuis une éternité (et figure dans le problème de john_john).
Il restera à trouver un cercle passant par $M^{\prime }$ et recoupant l'hyperbole aux centres des triangles équilatéraux de sommets $M$ inscrits dans l'hyperbole; le résultat est très simple.
Amicalement. Poulbot -
Bonjour Poulbot,
Merci beaucoup pour tes compléments, je vais étudier ça dès que je trouve un peu de temps libre.
PS : Quel logiciel utilises-tu pour tes figures ? -
Bonjour
$H$ est une hyperbole équilatère de centre $O$; $M\in H$, $M^{\prime }$ est le symétrique de $M$ par rapport à $O$ et $\overrightarrow{O\Omega }=-\dfrac{1}{3}\overrightarrow{OM}$.
Le cercle de centre $\Omega $ passant par $M^{\prime }$ recoupe $H$ aux centres des triangles équilatéraux de sommet $M$ inscrits dans $H$ (quand il y en a $3$, leur orthocentre est $M$).
@Mieses En général, je fais mes figures avec Cabri, histoire de me forcer, dans la mesure du possible à faire des figures sans utiliser de coordonnées, d'équations, … bref, à faire de la géométrie.
Amicalement. Poulbot -
Bonsoir à tous,
Comme je suis de la vieille école, je vous propose la bonne vieille méthode.
Je nomme $y_1,y_2,y_3,t$ les ordonnées de quatre points de la parabole d'équation $y^2=2px$, soit $x=\dfrac {y^2} {2p}$ et soit $(C)$ le cercle d'équation $x^2+y^2-2ax-2by+c=0$. Les 4 points cités sont sur le cercle $(C)$ ssi les ordonnées $y_1,y_2,y_3,t$ sont les racines de l'équation : $\dfrac {y^4}{4p^2}+y^2(1-\dfrac a p)-2by+c=0$
Notant $$\sigma_1=y_1+y_2+y_3,\ \ \ \sigma_2=y_1y_2+y_1y_3+y_2y_3,\ \ \ \sigma_3=y_1y_2y_3$$ et écrivant les relations entre coefficients et racines, on obtient:
$$ \sigma_1+t=0,\ \ \ \sigma_2+t\sigma_1=4p^2(1-\dfrac a p),\ \ \ \sigma_3+t\sigma_2=8p^2b$$ et une quatrième relation ($t\sigma_3=4p^2c$) inutile.
Maintenant déplaçons l'origine au centre $(a,b)$ du cercle (C). les trois premiers points auront pour ordonnées $z_1=y_1-b,\ \ ,z_2=y_2-b,\ \ ,z_3=y_3-b$. Ils forment un triangle équilatéral si la somme des $z_i$ est nulle et si la somme de leur produit 2à2 l'est également (facile à voir avec les nombres complexes). Ceci se traduit en deux conditions sur les$y_i$ : $$\sigma_1-3b=0,\ \ \ \ \sigma_2-2b\sigma_1+3b^2=0$$
La mise en place est terminé. Je pense que cela va rappeler de bons souvenirs à Poublot et à Pappus que je saluent respectueusement.
Bon, je veux bien finir à condition de savoir à quelle question je dois répondre. Le problème dépend d'un paramètre qui peut être $\sigma_3$. Le remplacement de $t$ par $-3b$ et $\sigma_1$ par $3b$, on oublie $\sigma_3$ puis ... finissez le boulot.
Cordialement,
zephir -
Merci Zephyr
Je suis très heureux que tu reviennes nous voir.
Comme Poulbot l'a dit, on a certainement parlé de ces triangles dans le passé dans un fil à retrouver!
Amicalement
[small]p[/small]appus -
Je termine. On rappelle les équations obtenues précédemment :
$$\sigma_1+t=0\ (1),\ \ \ \sigma_2+t\sigma_1=4p^2(1-\dfrac a p)\ (2),\ \ \ \sigma_3+t\sigma_2=8p^2b\ (3)\ \ \ \sigma_1-3b=0\ (4),\ \ \ \sigma_2-2b\sigma_1+3b^2=0\ (5)$$
et l'inutile : $t\sigma_3=4p^2c\ (6)$
(4) et (1) donnent : $\sigma_1=3b\ \ \ t=-3b$. (5) donne :$\sigma_2=2b.3b-3b^2=3b^2$. Reporté dans (2), on a la relation entre $a$ et $b$, tout calculs faits: $$3b^2=2p(a-p)$$. Le centre du cercle décrit la parabole annoncée.
Ayant choisi $b$, on aura :$\sigma_1=3b,\ \ \sigma_2=3b^2,\ \ \sigma_3=8p^2b+9b^3$.
Les ordonnées $(y_1,y_2,y_3)$ seront les solutions de l'équation :$(y-b)^3-8b(b^2+p^2)=0$. Les trois points forment bien un triangle équilatéral.
ouff !
C'est joli, c'est clair, net et sans bavure. C'est ce que les anciens m'ont appris et j'ai aimé cette géométrie analytique où on commence par faire un détour pour mieux et vite arriver au résultat
Cordialement,
zephir. -
Bonjour Zephir
Merci pour ce vent léger venu du passé.
Amicalement. Poulbot
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.2K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 65 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 314 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres



