Sécante focale d'une hyperbole

Bonsoir,

Voici une configuration tirée d'un problème du Bac 1950.
Dans le repère ci-dessous, on donne une hyperbole $\mathcal{H}$ de foyer $O$, de sommet $A(6;0)$ et de directrice $(d) : \, x=3$ associée à ce foyer.

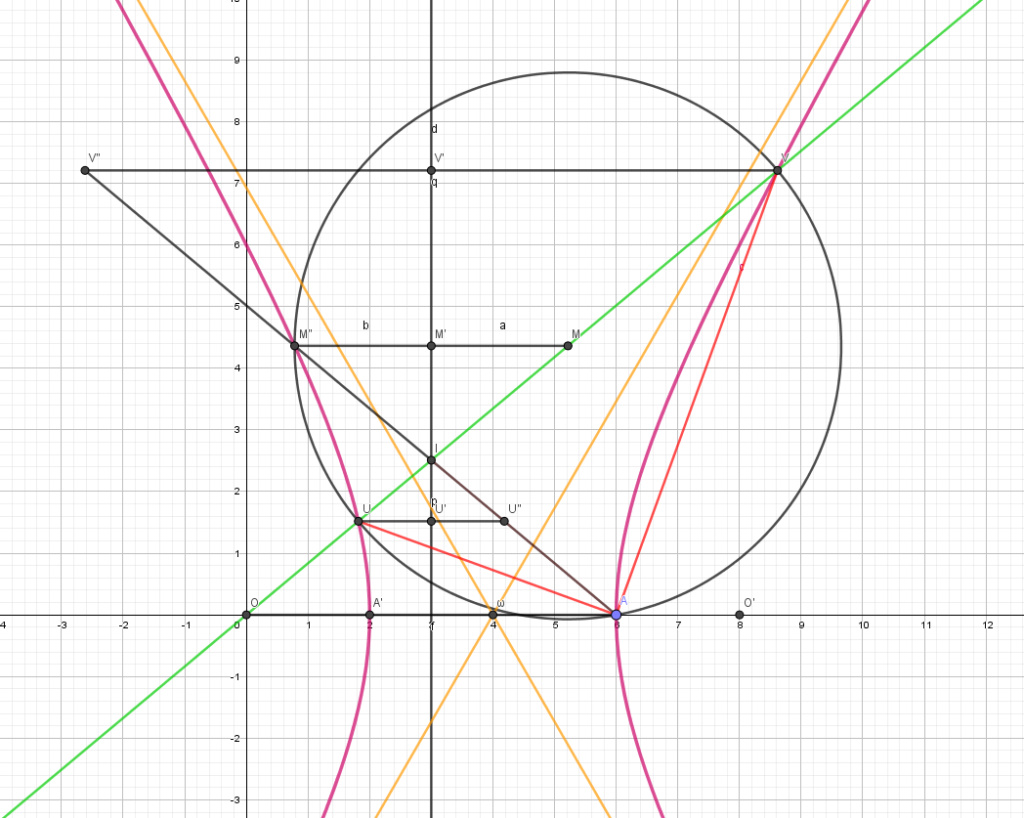
Une droite passant par $O$ coupe $\mathcal{H}$ aux points $U$ et $V$ et $(d)$ au point $I$. On note $U'$ et $V'$ les projetés orthogonaux respectifs de $U$ et $V$ sur $(d)$, puis $U''$ et $V''$ les symétriques respectifs de $U$ et $V$ par rapport à $(d)$.

On demande de démontrer que les droites $(AU)$ et $(AV)$ sont les bissectrices de l'angle $\widehat{IAO}$ ce que j'ai réussi à faire en traquant les triangles isocèles.
Ensuite on introduit le point $M$, milieu de $[UV]$. On note $M'$ son projeté orthogonal sur $(d)$ et $M''$ son symétrique par rapport à $(d)$. On demande de démontrer que $MA=2MM'$ ($2$ est l'excentricité de $\mathcal{H}$), ce qui revient à montrer que les points $V, A, U$ et $M''$ sont cocycliques.

Il me semble qu'il devrait y avoir une démonstration assez simple sans recourir à l'analytique en exploitant que les bissectrices divisent harmoniquement $[OI]$, mais je tourne en rond... Merci pour votre aide !