Correction de perspective
Bonjour,
Je me suis inscrit à ce forum pour faire appel à vos lumières au sujet d’un problème qui découle d’une application pratique sur laquelle je travaille : je souhaite corriger la perspective des photos de plans sur lesquels, après correction, je veux faire des mesures. Bien que j’aie déjà obtenu quelques résultats, il me manque les bases mathématiques pour bien comprendre les limites de la problématique. Je me suis penché sur les concepts de la géométrie projective (birapport, coordonnées homogènes) mais il me semble que ce ne sont pas les outils dont j’ai besoin. Je précise que je ne suis pas mathématicien, et, bien que j’aie quelques bons restes de mes lointaines études, le domaine de la géométrie projective est tout nouveau pour moi.
Voici donc mon problème : soit la projection connue sur un plan d’un rectangle de l’espace. Si elles existent, quelles sont les informations complémentaires minimums du plan de projection dont j’ai besoin pour retrouver les proportions du rectangle ?
En introduisant la projection orthogonale du centre de projection (qui pour une photo non recadrée correspond à son centre) il me semble qu’on peut retrouver les proportions seulement si les 2 points de fuite des cotés opposés ne sont pas à l’infini (ou sont tous les 2 à l’infini, mais dans ce cas là c’est facile…). Si c’est exact j’aimerais vraiment savoir pourquoi.
Merci pour toute information ou suggestion que vous pourrez me communiquer sur ce sujet.
Je me suis inscrit à ce forum pour faire appel à vos lumières au sujet d’un problème qui découle d’une application pratique sur laquelle je travaille : je souhaite corriger la perspective des photos de plans sur lesquels, après correction, je veux faire des mesures. Bien que j’aie déjà obtenu quelques résultats, il me manque les bases mathématiques pour bien comprendre les limites de la problématique. Je me suis penché sur les concepts de la géométrie projective (birapport, coordonnées homogènes) mais il me semble que ce ne sont pas les outils dont j’ai besoin. Je précise que je ne suis pas mathématicien, et, bien que j’aie quelques bons restes de mes lointaines études, le domaine de la géométrie projective est tout nouveau pour moi.
Voici donc mon problème : soit la projection connue sur un plan d’un rectangle de l’espace. Si elles existent, quelles sont les informations complémentaires minimums du plan de projection dont j’ai besoin pour retrouver les proportions du rectangle ?
En introduisant la projection orthogonale du centre de projection (qui pour une photo non recadrée correspond à son centre) il me semble qu’on peut retrouver les proportions seulement si les 2 points de fuite des cotés opposés ne sont pas à l’infini (ou sont tous les 2 à l’infini, mais dans ce cas là c’est facile…). Si c’est exact j’aimerais vraiment savoir pourquoi.
Merci pour toute information ou suggestion que vous pourrez me communiquer sur ce sujet.
Réponses
-
Ai-je bien compris ?
Tu photographies une figure plane et, en faisant des mesures sur la photo,
tu aimerais retrouver la figure d'origine, à un changement d'échelle près ? -
Oui, en pratique c’est bien ça, avec la préoccupation de bien connaître les limites théoriques de la procédure pour être sûr des résultats.
-
Bonjour
Ne manquerait-il pas des données comme celles que je suggère sur ma figure?
$HF=a$, $GE=b$, $\frac b a=\frac{OQ}{OF}=(Q,F,O,\infty)=(q,f,o,i)$
Amicalement
[small]p[/small]appus -
L'image d'un rectangle ne suffit pas pour retrouver les proportions de l'original.
Pour les photos déjà prises pappus a peut-être une idée.
Pour les photos encore à prendre le plus simple est probablement de les entourer
d'un cadre rectangulaire où figurent les milieux des quatre côtés.
Ce cadre entourant le plan sera grand et permettra une bonne précision.
On peut aussi marquer ces huit points au crayon et les effacer après avoir
pris la photo. Je noterais aussi les proportions du cadre sur le plan ou sur la photo.
Tiens-nous au courant. -
Merci soland et pappus d’avoir pris la peine de me proposer une solution. Il est clair que si on indique la largeur du rectangle sur sa longueur on retrouve facilement ses proportions. C’est bien une information mais j’ai bien peur de ne pas la trouver dans mes photos.
Sauf erreur, soland, le fait de connaître le milieu des côtés du rectangle ne permet pas de retrouver ses proportions.
En fait, mon application concerne des photos déjà prises, c’est pourquoi je m’intéresse plus particulièrement à la projection perpendiculaire du centre de projection. J’ai écrit un programme qui recherche la correction de perspective redonnant des côtés parallèles et quand j’introduis ce point au bon endroit, dans certaines conditions, je retrouve bien les proportions du rectangle que j’avais projeté préalablement.
Aussi, ce que j’aimerais comprendre c’est quelles sont les propriétés de ce point qui font que l’on peut retrouver dans certaines conditions les proportions du rectangle et bien sûr, en complément, quelles sont ces conditions.
Merci pour toute suggestion ou piste pour m’aider à voir clair dans ce problème. -
Bonjour Yvon_M
Regarde cette discussion:
Points Focaux
où tu apprendras comment l'aviation américaine redressait (localement la perspective de ses photos aériennes pendant la guerre $39-45$!
Amicalement
[small]p[/small] -
Bonsoir papus,
Merci pour le lien mais comment dire ? hé bien, à première lecture je n’ai pu que constater que le niveau était bien au dessus de mon seuil de compréhension…
Bon, je pense toutefois avoir compris que le redressement de la perspective était simplifié sur une partie locale de la photo et, sauf erreur, cela ne peut pas apporter de réponse à mon problème qui concerne des points quelconques sur la photo… à moins qu’il y ait dans vos différentes démonstrations certaines notions qui pourraient me servir. Dans ce cas, si vous voulez bien me les indiquer, je me pencherai de façon plus appliquée sur celles-ci.
Cordialement -
Bonjour
Je pense que si la photo contient l'image d'un carré ou d'un cercle on doit pouvoir s'en sortir comme je l'ai suggéré sur ma figure.
Au voisinage du point focal de la photo, on détermine un tel cercle ou un tel carré, par exemple un petit cercle centré sur le point focal, dont on se sert ensuite pour redresser la photo plus globalement?
Il doit y avoir des livres qui donnent des programmes sur ce sujet auquel je ne connais rien
Amicalement
[small]p[/small]appus -
Bonjour Yvon_M
Dans mon fil sur les points focaux, je montre que la connaissance des points focaux directs et indirects et de leurs images suffit à déterminer complètement une transformation projective plane.
On a même une construction à la règle et au compas d'un point et de son image!
Je suppose qu'il en est de même pour une transformation projective d'un plan sur un autre. A vrai dire je n'y ai pas réfléchi!
J'avais un peu oublié ce fil et en fait j'ai fait:
l'épure de cette transformation
Mais si l'U.S Air Force s'intéressait tant à ces points focaux c'est qu'il y avait une bonne raison!
Amicalement
[small]p[/small]appus -
Je pense avoir avancé sur la résolution de mon problème. Je vous présente sans trop de recul le résultat auquel je suis parvenu, n’hésitez pas à le critiquer. Il y a certainement des parallèles à faire avec le fil de pappus sur les points focaux, ce que j’envisage de faire maintenant que certains concepts commencent à m’être plus familiers. Pour la résolution, j’ai utilisé la géométrie classique.
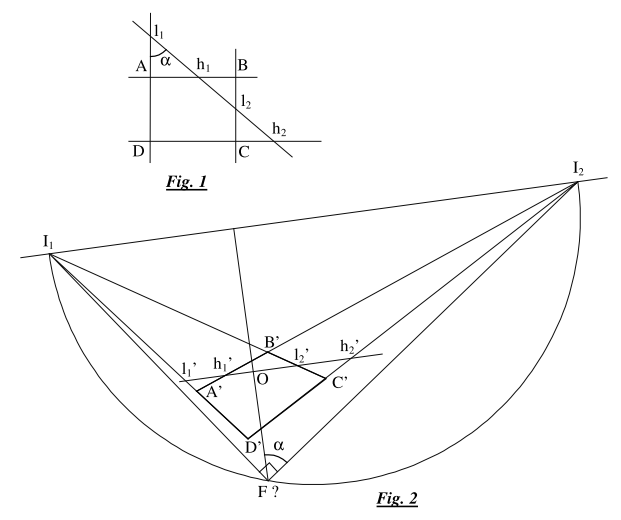
Soit donc, Fig. 1, le rectangle $ABCD$ initial. Posons $l = AB$ et $h = AD$, on cherche le rapport $\frac{l}{h}$.
Soient, Fig. 2, la photo $A’B’C’D’$ du rectangle et $O$ le centre de la photo. On détermine les 2 points de fuite $I_1$ et $I_2$ par lesquels on trace la droite à l’infini. Du point $O$ on trace une parallèle qui coupe les côtés du rectangle (éventuellement prolongées) aux points $l’_1, l’_2, h’_1$ et $h’_2$. Sur cette droite on a l’égalité des rapports :
$$\frac{l’_1l’_2}{h’_1h’_2}=\frac{l_1l_2}{h_1h_2}=\frac{l/sin\alpha}{h/cos\alpha}$$
d’où :
$$\frac{l}{h}=tan\alpha\frac{l’_1l’_2}{h’_1h’_2}$$
Il nous reste à déterminer l’angle $\alpha$. Pour cela on cherche sur la perpendiculaire à la droite à l’infini passant par $O$ le point $F$ d’où les points de fuite sont vus sous un angle de 90° (il me semble que c’est un point focal, est-ce que je me trompe ?). On peut trouver ce point en traçant le demi-cercle $I_1FI_2$. L’angle $\alpha$ cherché est l’angle $OFI_2$.
Cordialement -
Mon cher Yvon_M
J'essaye de comprendre ce que tu as fait!
Mais tout d'abord, comment définis-tu le centre de la photo?
Amicalement
[small]p[/small]appus -
Bonsoir pappus,
Mathématiquement le point O correspond à la projection perpendiculaire sur le plan de la projection du centre de la projection. En photographie le centre de projection est le centre de l'optique qui est situé sur la normale au centre de la photo quand celle-ci n'a pas été recadrée.
Je suis ravi que mon petit problème vous intéresse.
Cordialement -
Merci Yvon_M
Pourquoi pas!
Maintenant j'essaye de comprendre la suite.
Tu as décidé de noter $f:M\longmapsto M'$ la transformation projective du plan $P$ contenant le rectangle $ABCD$ sur le plan $P'$ de la pellicule photographique contenant l'image $A'B'C'D'$.
Techniquement c'est une homologie de pôle le centre de l'optique $O$.
Je m'intéresse d'abord à tes deux points de fuite que tu as noté $I_1$ et $I_2$, ils appartiennent au plan $P'$.
Tu aurais dû les primer $I'_1$ et $I'_.2$ car ce sont les images par $f$ de points (à l'infini) $I_1$ et $I_2$ du plan $P$.
La droite que tu appelles $I_1I_2$ joignant les points de fuite $I_1$ et $I_2$ n'est pas la droite de l'infini du plan $P'$ mais l'image par $f$ de la droite de l'infini du plan $P\ $.
On l'appelle la ligne de fuite (de la perspective).
Enfin je m'intéresse à la droite $h_1h_2$ du plan $P$ et à son image $h'_1h'_2$ du plan $P'$.
Quelle est leur situation dans l'espace pour que tu puisses écrire:
$\dfrac{I'_1I'_2}{h'_1h'_2}=\dfrac{I_1I_2}{h_1h_2}$?
Enfin tes points $I_1$ et $I_2$ apparaissent deux fois, une fois dans le plan $P$ et une fois dans le plan $P'$, c'est une fois de trop, il va falloir choisir!
Amicalement
[small]p[/small]appus -
Cher pappus,
Merci pour vos remarques qui me permettront d’être plus rigoureux à l’avenir.
Pour votre dernière question, il s’avère que je n’ai pas été très judicieux dans le choix de mes lettres repères en choisissant le L minuscule (pour « longueur ») qui se confond facilement avec le I majuscule. Du coup, j’ai modifié le message de ma démonstration en utilisant les directives LaTeX (je n’avais pas encore compris comment les utiliser), ce qui permet de mieux les distinguer.
Cordialement
Yvon -
Bonjour Yvon_M
Tu dis que tu as pris note de mes remarques mais tu n'as pas modifié l'étiquetage de ta figure et la droite $I_1I_2$ est toujours la droite de l'infini (d'on ne sait quoi!) alors qu'elle est la ligne de fuite de la perspective!
Tu n'échapperas pas à l'explication de l'égalité:
$$\dfrac{I'_1I'_2}{h'_1h'_2}=\dfrac{I_1I_2}{h_1h_2}$$
Amicalement
[small]p[/small]appus -
Cher pappus,
Par facilité j’avais simplement repris mon message de jeudi dernier sans trop le modifier pour que les futurs lecteurs de ce fil s’y retrouvent. Mais vous avez raison, la rigueur est une discipline à part entière qui demande des sacrifices. Aussi j’ai repris ci-dessous ma figure, suivant vos recommandations et en utilisant des lettres repères qui ne prêtent pas à confusion, ainsi que le texte de ma démonstration. J’en ai profité pour rajouter quelques détails supplémentaires.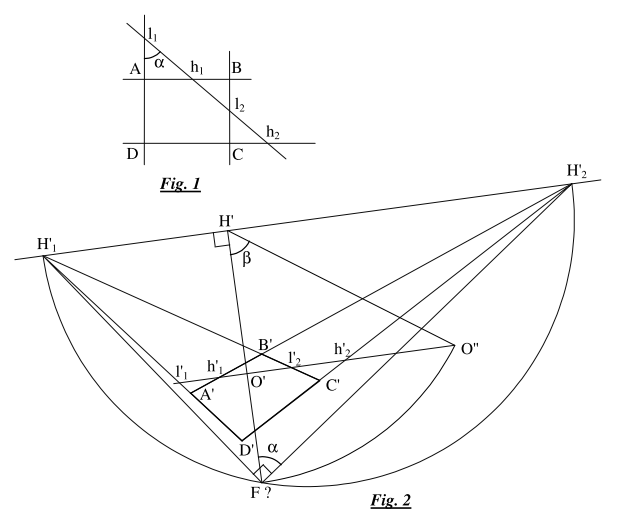
Soit, Fig. 1, le rectangle $ABCD$ initial. Posons $l=AB$ et $h=AD$, on cherche le rapport [large]$\frac{l}{h}$[/large].
Soient, Fig. 2, la photo $A'B'C'D'$ du rectangle et $O'$ le centre de la photo qui correspond à la projection orthogonale du centre optique $O$ sur la photo quand celle-ci n’a pas été recadrée. On détermine les 2 points de fuite $H'_1$ et $H'_2$ par lesquels on trace la ligne de fuite. Du point $O’$ on trace une parallèle qui coupe les côtés du rectangle (éventuellement prolongées) aux points $l'_1$, $l'_2$, $h'_1$ et $h'_2$. Sur cette droite, comme sur toutes les droites qui lui sont parallèles, on a l’égalité des rapports :
$$\frac{l'_1l'_2}{h'_1h'_2}=\frac{l_1l_2}{h_1h_2}=\frac{l/\sin\alpha}{h/\cos\alpha}$$
d’où :
$$\frac{l}{h}=\tan\alpha\frac{l'_1l'_2}{h'_1h'_2}$$
Il nous reste à déterminer l’angle $\alpha$. Pour cela on cherche, sur la perpendiculaire à la ligne de fuite passant par $O'$, le point $F$ d’où les points de fuite sont vus sous un angle de 90° (il me semble que c’est un point focal, est-ce que je me trompe ?). On peut trouver ce point en traçant le demi-cercle $H'_1FH'_2$. L’angle $\alpha$ cherché est l’angle $O'FH'_2$.
De plus si on trace le cercle de centre $H'$ passant par $F$ on détermine, à l’intersection de la parallèle à la ligne de fuite passant par $O'$, le point $O''$ tel que $O'O''=O'O$. Par ailleurs l’angle $\beta$ correspond à l’angle dièdre entre le plan de la photo et celui du rectangle $ABCD$.
Bien cordialement
Yvon -
Mon cher Yvon_M
Je suis très heureux de pouvoir dialoguer avec toi et nous avons beaucoup à apprendre l'un de l'autre.
Es-tu déjà un professionnel ou encore étudiant dans une école enseignant l'art de la photo?
Je suppose que tu connais quelques lois de la perspective?
As-tu appris des rudiments de géométrie descriptive?
Tes questions sont très intéressantes et rejoignent celles que se posaient les officiers de renseignement américains pendant la guerre contre les nazis pour faire parler les photos aériennes dont ils disposaient.
Ceux-ci étaient sans doute frais émoulus de leurs universités où ils avaient appris la géométrie projective et l'US Air Force était bien contente de profiter de leurs compétences.
Je me demande même si ce ne sont pas ces tristes circonstances qui ont permis la création du concept des points focaux.
Je ne pense pas que nous en ayons besoin aujourd'hui mais sait-on jamais.
J'ai repris ta photographie dans mon dessin ci-dessous sans reprendre sa partie haute, à savoir le rectangle $ABCD$.
Après tout, c'est ce qui se passait autrefois, on devait interpréter les photos à des centaines de kilomètres de l'endroit où elles avaient été prises.
Je me suis demandé si on avait vraiment besoin dans un premier temps de ce que tu appelles le centre de la photographie.
J'ai tracé deux transversales parallèles à la ligne de fuite $I'_1I'_2h'_1h'_2$ et $J'_1J'_2k'_1k'_2$ et je prétends qu'on a toujours:
$$\dfrac{\overline{I'_1I'_2}}{\overline{h'_1h'_2}}=\dfrac{\overline{J'_1J'_2}}{\overline{k'_1k'_2}}$$
[large]Pourquoi?[/large]
Donc pour ce qu'on a à en faire, que cette transversale $I'_1I'_2h'_1h'_2$ passe ou non par ce que tu appelles le centre de la photographie n'a strictement aucune importance!
Par contre tu n'as toujours pas démontré l'égalité très importante dont tu te sers dans la suite:
$$\dfrac{\overline{I'_1I'_2}}{\overline{h'_1h'_2}}=\dfrac{\overline{I_1I_2}}{\overline{h_1h_2}}$$
Tu l'as simplement affirmée au point qu'on a le sentiment qu'elle te parait évidente et allant de soi!
Pourquoi?
Amicalement
[small]p[/small]appus -
Cher pappus,
Je réponds à vos question dans l’ordre :Es-tu déjà un professionnel ou encore étudiant dans une école enseignant l'art de la photo?
Un professionnel qui approche de la retraite, plus exactement un ingénieur en électronique. Ma formation s’est faite par la filière technique, simplement pour dire que l’enseignement des mathématiques que j’ai reçu était assez orienté vers les aspects pratiques.Je suppose que tu connais quelques lois de la perspective?
Oui, mais comme je le disais plus haut, je me suis penché sur cette discipline récemment.As-tu appris des rudiments de géométrie descriptive?
À l’école, non. Mais le centre d’intérêt de mes loisirs est depuis longtemps orienté sur la gnomonique ou science des cadrans solaires. Dans ce domaine j’ai lu beaucoup d’anciens ouvrages où on utilise une géométrie assez particulière qui consiste à rabattre les plans sur celui de la figure. C’est ce type de géométrie que j’ai utilisé.
Pour en savoir plus sur l’origine de ma question vous pouvez aussi consulter ce fil qui fait partie d’un forum que j’administre.on a toujours:
$$\frac{I'_1I'_2}{h'_1h'_2}=\frac{J'_1J'_2}{k'_1k'_2}$$
Pourquoi?
Nous confondrons pour la suite vos I majuscules avec mes L minuscules et nous sommes bien d’accord que l’axiome de Thalès suffit pour établir cette relation.$$\frac{I'_1I'_2}{h'_1h'_2}=\frac{I_1I_2}{h_1h_2}$$
Tu l'as simplement affirmée au point qu'on a le sentiment qu'elle te parait évidente et allant de soi! Pourquoi?
Toute droite parallèle à la ligne de fuite peut être considéré comme l’intersection du plan de la photo avec un plan $P''$ parallèle à celui du rectangle $ABCD$. Les droites de projection (corrigez-moi si le terme n’est pas correct), qui passent par $O$ et les point $A$, $B$, $C$ et $D$, coupent $P''$ en $A''$, $B''$, $C''$ et $D''$. Ces points forment un rectangle similaire à $ABCD$ qui passe par les points $l'_1$, $l'_2$, $h'_1$ et $h'_2$ d’où l’égalité proposée.
Bien cordialement
Yvon -
Merci Yvon_M
Pas mal du tout et Bravo!
Tu te débrouilles pas mal.
On passe à la dernière partie de tes affirmations, la construction de l'angle $\alpha$.
On sent qu'il y a du rabattement dans l'air comme tu le dis.
Mais j'avoue n'avoir pas compris ta construction!
Pourquoi le cercle de diamètre $H'_1H'_2$ contribue -t-il au rabattement du point $O$? Mystère et Boule de Gomme!
Il faut absolument nous dire pourquoi!
Et surtout surtout pourquoi rabattre ce point plutôt qu'un autre alors que les sommets du rectangle $ABCD$ nous tendaient les bras comme le point $D$ par exemple. Dans son rabattement autour de $H'_1H'_2$, le point $D$ se rabat justement en point du cercle de diamètre $H'_1H'_2$ à cause de la présence de l'angle droit au sommet $D$ du rectangle $ABCD$.
J'ai bien l'impression que le point $O'$ ne joue aucun rôle dans ta construction.
Par contre ce point $O'$ joue un rôle dans la construction des points focaux de la perspective comme je l'ai montré dans ma discussion sur les points focaux.
Puisque la géométrie a été d'abord une science de la mesure, peux-tu confirmer expérimentalement que ta construction donne la bonne proportion pour le rectangle!
Amicalement
[small]p[/small]appus -
Cher pappus,
La réponse à vos questions est relativement simple : le rabattement que l’on peut effectuer avec pour « charnière » la ligne de fuite ne peut être qu’un plan parallèle à $P$ et qui passe par $O$. Pour rabattre le plan $P$ du rectangle il faudrait connaître son intersection avec le plan $P'$ de la photo, c’est une parallèle à la ligne de fuite mais on ne connaît pas sa position.
Par ailleurs, oui, j’ai confirmé expérimentalement que l’on retrouve bien les proportions du rectangle (je n’aurais pas osé présenter des résultats dont je n’étais pas au moins convaincu).
En complément, on peut montrer théoriquement avec la figure proposée qu’on ne peut pas retrouver ces proportions quand un seul des 2 points de fuite est à l’infini, ce que j’avais constaté expérimentalement.
Je ne sais pas s’il est d’usage entre mathématicien de poser toutes ces questions. Si c’est le cas je veux bien m’y conformer à mon tour :
Je confirme mon intuition que le point F est bien un point focal, pourquoi ?
J’avoue que je n’ai pas relu le fil où vous développez les propriétés des points focaux et où vous apportez peut-être la réponse mais j’ai acquis cette conviction uniquement à l’aide de la figure que j’ai proposée.
Bien cordialement
Yvon -
Mon cher Yvon_M
J'ai réussi à faire l'épure de ta configuration et j'ai pu vérifier ta construction de l'angle $\alpha$.
Félicitations!
Elle marche, même si je n'ai pas encore compris pourquoi!
L'épure est très difficile à faire si on veut qu'elle soit lisible.
J'attends que ce soit le cas avant de l'éditer.
Amicalement
[small]p[/small]appus -
Bonjour
Voici l'épure de la configuration d'Yvon_M!
J'en ai bavé pour la rendre lisible!
J'ai appris la géométrie descriptive, il y a 70 ans et j'en ai refait, il y a 10 ans.
J'avais largement le temps d'oublier.
J'ai l'impression de dénuder une vieille momie.
Le plan de la photo est le plan horizontal de projection.
Le plan à photographier est le plan debout $P'$.
Le pôle de la projectivité est le point $(o,o')$.
J'ai malheureusement dû changer les notations puisqu'un point de l'espace est repéré par ses projections horizontale et frontale.
On voit la construction d'Yvon sur la gauche avec le point $f$.
J'avais cru qu'il était un rabattement du point $O'$, en fait il n'en est rien!
C'était là mon incompréhension!
La validité de la construction d'Yvon_M se traduit par les parallélismes $H_1f\parallel a_2d_2$ et $H_2f\parallel a_2b_2$
Amicalement
[small]p[/small]appus
PS
Pour la compréhension de l'épure, désolé mais j'ai la flemme de refaire un cours de descro.
On trouvera néanmoins quelques indications dans le fil sur les points focaux dont j'ai donné le lien un peu plus haut.
Le point $f\ $ est bien l'un des quatre points focaux, bravo Yvon_M!
Il y a deux points focaux situés dans le plan horizontal de projection, c'est à dire le plan de la photo, l'un est le point $f$, l'autre est le symétrique de $f$ par rapport à la ligne de fuite que j'ai tracée en rouge pointillé un peu épais. Je n'ai pas tracé ce symétrique!
C'est extraordinaire que la construction d'Yvon_M permette de récupérer ces points focaux directement sur la photo.
C'est le théorème d'Yvon_M:
Les cercles de diamètre $H_1H_2$ forment un faisceau à points de base les deux points focaux
Ce qui entraîne que les points $H_1$ et $H_2$ sont en involution sur la ligne de fuite!
Je suis à peu près sûr que les officiers de renseignement américains connaissaient cette construction, il n'y a jamais rien de nouveau sous le soleil de la géométrie!
Quant à nous, on fait mumuse avec les axiomes de Thalès et de Pythagore et en plus il faut être contents!!
@Yvon_M
Bravo pour ton site!
J'espère que notre discussion permettra une amélioration dans le traitement de tes photos.
Je suis admiratif devant ta virtuosité qui t'a permis de retrouver les points focaux si naturellement! -
Bonjour à tous
Par acquit de conscience, je redonne l'épure d'un point $(n,n')$ et de son image $(m,m')$ dans la projectivité (photographique).
C'est plus ou moins celle qui date de dix ans dans le fil sur les points focaux.
Elle fait intervenir le pôle $(o,o')$ où $o'$ est le centre de la photo et les points focaux $f_1$ et $f_2$ situés dans le plan de la photo.
C'est cette construction de ces deux points focaux qui est due aux américains.
Le plus incroyable, c'est qu'Yvon a fait cette figure et que dix ans après, j'ai été infoutu d'y reconnaître la mienne!
La ligne de rappel en rouge pointillé épais est la ligne de fuite.
Amicalement
[small]p[/small]appus -
Bonjour
Sur mon avant-dernière épure concernant la photographie $A'B'C'D'$ du rectangle $ABCD$, j'ai modifié certaines étiquettes pour les rendre conformes à celles d'Yvon et j'ai pu ainsi faire apparaître en rouge épais sa figure n°2.
Et c'est ce que je n'avais pas vu.
La figure n°2 d'Yvon faisait partie de mon épure.
J'ai bien mis une bonne journée avant de le comprendre!
Il fallait faire l'épure pour comprendre la figure d'Yvon!
J'ajoute que contrairement à ce que je pensais au premier abord, ce qu'Yvon appelle le centre de la photo joue un rôle primordial dans sa construction! Mais comment le récupère-t-on pratiquement?
Amicalement
[small]p[/small]appus -
Cher pappus,
Merci pour vos compliments qui me touchent beaucoup sachant qu’ils viennent d’un expert. Merci aussi d’avoir pris la peine de dessiner cette épure pour faire le parallèle avec la figure que j’ai faite, ainsi les deux approches s’éclairent mutuellement.
Fort des conseils de rigueur que vous m’avez dispensés je me permettrai même de proposer quelques petites corrections. Je précise que ce ne sont que des points de détail qui n’empêchent absolument pas de comprendre la figure :- Le segment $ab$ est inutile
- Le segment $dd'$ pourrait être rajouté en pointillé rouge
- Le trait noir épais devrait s’appeler $P$
Voici aussi quelques éclaircissements pour mieux comprendre la figure que j’ai proposée. Elle comporte 2 « rabattements ». Ce que j’appelle rabattement consiste à faire pivoter un plan autours d’une ligne de la figure (dans notre cas de la photo) pour l’appliquer sur celle-ci.
Comme indiqué plus haut, le premier rabattement est celui du plan parallèle au plan $P$ et qui passe par le centre de la projection, il passe donc par la ligne de fuite autour de laquelle ont fait le rabattement. Dans celui-ci on cherche le point $O$ (que j’ai en fait appelé $F$) qui, d’après ce que je me souvenais de la perspective, permet de graduer la ligne de fuite en angle (Ozanam a baptisé ce type de point un centre diviseur) et trouver l’angle $\alpha$. D’où la recherche d’un angle droit à partir des points de fuite $H'_1$ et $H'_2$, qui répondent aux angles droits du rectangle $ABCD$, sur la perpendiculaire $O'H'$.
Le second rabattement, qui est effectué suivant la ligne $H'F$, est celui du plan perpendiculaire à la photo, ce plan contient aussi le point $O$ et on détermine sa distance à $O'$ en faisant correspondre $F$ et $O''$. On obtient ainsi sur ce rabattement l’angle dièdre $\beta$ entre les plans $P$ et $P'$.
Enfin, puisque j’ai posé une question, je donne ici ma réponse à partir des rudiments de géométrie que je connais :
J’avais connaissance de la propriété suivante : soient 2 plans différents non parallèles de l’espace, il existe deux et seulement deux directions de projection parallèle d’un plan sur l’autre donnant une isométrie. Par symétrie on comprend facilement que ces directions sont les perpendiculaires aux 2 plans bissecteurs des plans de projection.
Dans notre problème de perspective les plans $P$ et $P'$ définissent ces 2 directions. Les points focaux sont donc sur les 2 droites qui passent par le centre de projection et qui correspondent à ces directions. À la différence de la projection parallèle nous n’aurons plus dans ce cas, au voisinage de ces droites, une isométrie mais une similitude.
Fort de cette certitude on voit bien sur le second rabattement que la droite $O''F$ correspond au rabattement d’un droite passant par le point $O$ et ayant une des directions qui définissent les point focaux. $F$ qui dans ce cas est considéré comme faisant partie de $P'$ est donc un point focal.
Encore merci pappus de vous être intéressé à mon petit problème. J’en ai un second concernant la perspective que je proposerai sur un nouveau fil, le temps de trouver un petit moment pour le formuler correctement.
Bien cordialement
Yvon -
Mon cher Yvon
C'est toi le véritable expert.
Tu sais appliquer la géométrie à un problème concret en véritable virtuose et je n'ai pas grand chose à t'apprendre.
Cette théorie des cadrans solaires est absolument passionnante aussi bien du point de vue scientifique que du point de vue historique.
Il va falloir que je m'y plonge!
Amicalement
[small]p[/small]appus
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.2K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 65 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 69 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 314 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres
