Question de raisonnement

raboteux · January 2020

Bonjour
Voici un problème de géométrie classique.

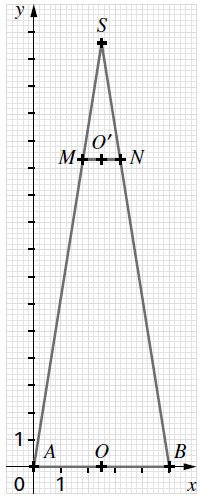
Le dessin ci dessus est une réduction à l'échelle 1/4
Les distances réelles sont :
OO'=45
AB=20
MN=5,5
O est milieu de [AB], O' est milieu de [MN] et (SO) est médiatrice de [MN] et [AB], enfin (MN) et (AB) sont parallèles.
L'énoncé de la question qui me préoccupe est "démontrer que $SO'\approx{17}$"

Alors, je n'ai pas de problème pour prouver rigoureusement cela avec Thalès appliqué dans les triangles SO'N et SOB.

Par contre, j'ai une connaissance qui raisonne comme ceci :
il part de : $\dfrac{SO'}{SO}=\dfrac{O'N}{OB}$
Puis il dit que : $SO=OO'+SO'=45+17=62$
Il en sort que : $SO'=\dfrac{SO\times{O'N}}{OB}=\dfrac{62\times{2,75}}{10}\approx{17}$

J'ai l'intuition que ce raisonnement est faux car la preuve qu'il utilise est basé sur la validé de la conclusion que l'on veut prouver (quand on utilise que : $SO=OO'+SO'=45+17=62$).
Mais j'ai encore à m'améliorer en pédagogie, donc j'aimerais votre avis sur les arguments précis à donner à cette personne...
Merci.

gerard0 · January 2020

Bonjour.

L'utilisation de la conclusion comme argument est évidemment une faute de logique, sinon tout est démontrable (pour démontrer A on utilise A et $A\Rightarrow A$).
J'espère que ton énoncé est plus précis que ce que tu en dis, car $SO'\approx 17$ est toujours vrai (par exemple à 100 près).

Cordialement.

raboteux · January 2020

Merci Gérard,

Et non l'énoncé n'est pas plus précis, ta remarque est fondée.

raboteux · January 2020

Est ce que l'on peut ici parler de "raisonnement circulaire"?

gerard0 · January 2020

Oui, c'est une des expressions qu'on emploie. Ça n'explique rien, mais ça donne une idée : On tourne en rond ("si conclusion, ... alors conclusion").

Dom · January 2020

Pour lui montrer qu’il y a un loup :
1)
pourquoi 45+17 ? (je suppose que c’est courant...)
2)
Si on remplace 45+17 par 45+18 on trouve encore « environ 17 ».
Bizarre non ? (On peut convenir que le « environ » est à l’entier près, Gérard a raison, il manque une phrase pour préciser cet « environ ».). Ou encore par $45+16,9$.
3) (zut urgence)

Une remarque : ici ce n’est pas le cas mais il existe des raisonnements de ce genre qui fonctionnent.
Un exemple : démontrer que la seule solution de l’équation d’inconnue $x$, $[8x=6]$ est $3/4$.
Rédaction valable :
C’est une équation équivalente à $[8x-6=0]$.
Je sais (théorème) qu’une équation d’inconnue $x$ du type $[ax+b=0]$ avec $a\neq 0$ et $b$ un nombre possède une solution et une seule.
Or : $8\times 3/4+6=0$.
Donc la seule solution est $3/4$.

En fait le « environ » fiche un peu tout par terre.

gerard0 · January 2020

Dom,

ce n'est pas un raisonnement circulaire car tu n'utilises ni "$\frac 3 4 $ est solution", ni "c'est la seule". tu les démontres effectivement. Tu te sers de l'énoncé de l'exercice pour le faire, mais on fait toujours ça (comment faire un exercice sans l'énoncé ?).

Il faut bien distinguer "utiliser l'énoncé de l'exercice pour le faire" et "utiliser la conclusion comme moyen de preuve".

Cordialement.

Dom · January 2020

Oui, oui,

Disons que dans la plupart des cas l’auteur aurait voulu que le candidat résolve « en vrai » l’équation.

On a les mêmes choses avec Pythagore : utiliser la longueur qu’il faut trouver est possible puisqu’il y a équivalence (sens direct, réciproque). En gros, trouver une valeur qui marche c’est trouver la valeur.

gerard0 · January 2020

Ça me rappelle la traditionnelle rédaction des exercices de résolution de l'équation du second degré quand j'étais lycéen (que j'ai évitée quand je suis devenu prof)
"Soit ..(équation du second degré)
1) L'équation a-t-elle des solutions.
2) Calculer les solutions de l'équation. "
Et la réponse qui faisait hurler les profs :
"1) Oui, puisqu'on dit dans la question 2 qu'elle en a.
2) ".

Cordialement.

Dom · January 2020

Oui. Là il y a une forme de malhonnêteté intellectuelle.

Par contre l’élève peut résoudre l’équation en 2) et répondre à la question 1) après.
Sans problème de raisonnement ni de provocation.

Le plus astucieux répondra aux deux questions en même temps, sans séparer les questions.

Foys · January 2020

Etant donné $y$, les énoncés $\forall x P(x)\Rightarrow x =y$ et $\forall x,\neg P(x) $ ne sont pas incompatibles (le deuxième entraîne d'ailleurs le premier).

pldx1 · January 2020

En fait, ce n'est pas un raisonnement circulaire, mais un raisonnement patatoïdal.

La première ligne de la "méthode alternative" est déjà fausse: $SO=45+17=62$ ne va pas. Puisque ce n'est pas 17, ce n'est pas 62 non plus. Quant à critiquer $\dfrac {495}{29} = 17.068965517241379310... \approx 17$, pourquoi pas, cela occupe.

Cordialement, Pierre.

raboteux · January 2020

Merci à tous pour votre aide.

Effectivement, sans utiliser d'autres considérations, est-ce que l'on ne peut pas dire que dans le cas présent, tout raisonnement exploitant la valeur finale comme argument est forcément faux, car ce n'est qu'une valeur approchée. Du coup, pourquoi prendre dans ces raisonnements là 17 plutôt que 16.5, plutôt que 17,3 pour SO'...

Une autre question : si l'énoncé avait été très légèrement différent (c'est-à-dire les valeurs données pour OO', AB et MN) pour permettre que le question soit : "démontrer SO'=17" (ici plus de "environ"), la situation aurait-elle été différente vis-à-vis de ces raisonnements?
Plus précisément, est-ce que les théorèmes de Thalès, ou [large]P[/large]ythagore (ou combinaison des deux) auraient pu être utilisés de quelconque manière pour démontrer le résultat en utilisant comme argument initial ou intermédiaire que SO'=17 ?

[ Pythagore (environ -580 ; -495) prend toujours une majuscule. AD]

Question de raisonnement

Réponses

Bonjour!

Catégories

In this Discussion

Qui est en ligne 33