Problème facile dans le plan euclidien

GaBuZoMeu
GaBuZoMeu
dans Géométrie
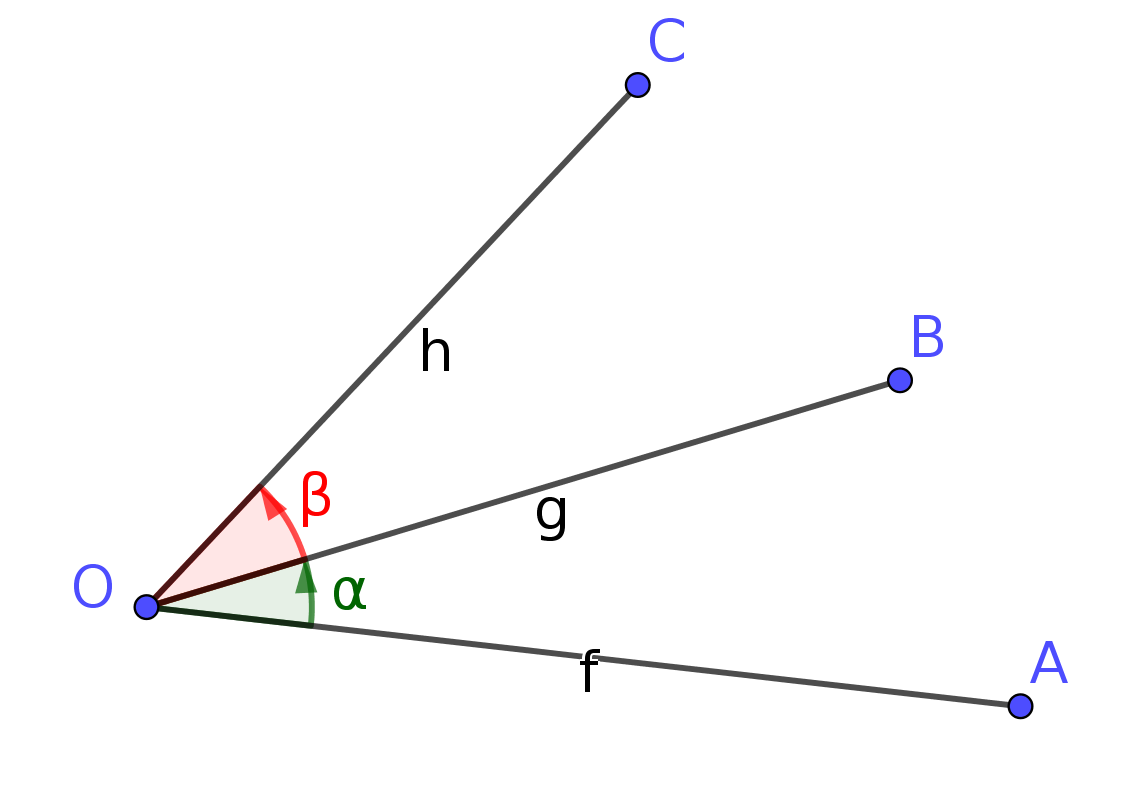
200402075826169730.png

$A,B,C$ dans le plan, $O$ distinct de $A,B,C$. Les points $A,B,C$ sont alignés si et seulement si
$$\frac{\sin(\alpha+\beta)}{g}= \frac{\sin(\alpha)}{h}+\frac{\sin(\beta)}{f}\;.$$
Quelle est votre démonstration préférée de ce résultat ?

Il y en a une que je préfère. Mais des goûts et des couleurs ...

Réponses

  • pappus
    pappus
    Mon cher GaBuZoMeu
    Merci de nous donner ce bel exercice.
    Je suppose que la preuve que tu préfères fait appel à l'additivité de la mesure?
    Amicalement
    [small]p[/small]appus
  • GaBuZoMeu
    GaBuZoMeu
    Ce n'est pas vraiment celle-là, mais elle n'en est pas loin.
  • pappus
    pappus
    Mon cher GaBuZoMeu
    Zut, je pensais avoir trouvé!
    Alors la Divine Trigonométrie et les diverses formules d'addition des arcs comme on disait autrefois?
    Je pense surtout à: $\sin(\alpha+\beta)=...$
    On va quand même pas passer toutes les démonstrations possibles en revue?
    Ca ne m'étonnerait pas que cela soit fait dans un livre de Perrin dont je ne me souviens plus du titre!
    Amicalement
    [small]p[/small]appus
  • pappus
    pappus
    Bonjour à tous
    Sinon on sort la très très grosse artillerie: Axiome de Thalès plus loi des sinus.
    C'est justement le moment de surveiller ses sinus!
    Amicalement
    [small]p[/small]appus99010
  • GaBuZoMeu
    GaBuZoMeu
    Cher Pappus,

    Là, tu refroidis. L'additivité de la mesure n'était vraiment pas loin de ce à quoi je pensais. Mais je la voyais dans l'espace ...
  • pappus
    pappus
    Merci GaBuZoMeu
    Alors là, je n'avais pas pensé à cela!
    Effectivement beaucoup de configurations planes s'expliquent plus facilement en les plongeant dans l'espace et je pense en particulier à celle de Desargues.
    Mais je te rappelle que ma prof de dessin de machines me disait souvent: vous serez toujours incapable de voir dans l'espace.
    Du tétraèdre dans l'air
    Le smoking de travers
    Je te suis pas dans cette galère
    Ta vie tu peux pas la refaire
    Amicalement
    [small]p[/small]appus
  • GaBuZoMeu
    GaBuZoMeu
    Non, pas de tétraèdre en fait.
    L'identité peut se mettre sous la forme
    $$ OA\times OB\times\sin(\vec{OA},\vec{OB})+OB\times OC\times\sin(\vec{OB},\vec{OC})+OC\times OA\times\sin(\vec{OC},\vec{OA})=0$$
    et le résultat apparaît comme un cas particulier du résultat à peu près trivial suivant :
    Soient $O,A,B,C$ quatre points de l'espace euclidien. Alors $A,B,C$ sont alignés si et seulement si
    $$\vec{OA}\wedge\vec{OB}+\vec{OB}\wedge\vec{OC}+\vec{OC}\wedge\vec{OA}=0\;.$$
    C'est à peu près trivial parce qu'il est à peu près trivial que le vecteur à gauche ne dépend pas de $O$ et qu'on peut par conséquent supposer $O=A$.

    Mais c'est juste un déguisement de l'additivité de la mesure dans le plan. En fait on peut prendre $O,A,B,C$ dans un espace affine quelconque $E$, et l'alignement de $A,B,C$ est équivalent à $\vec{OA}\wedge\vec{OB}+\vec{OB}\wedge\vec{OC}+\vec{OC}\wedge\vec{OA}=0$ dans $\bigwedge^2(\vec{E})$.
  • Chaurien
    Chaurien
    La mesure ? Quelle mesure ?
  • pappus
    pappus
    Mon cher Chaurien
    La mesure de Lebesgue évidemment, lui qui était avant tout un géomètre dans l’âme!
    Amicalement
    [small]p[/small]appus
  • pappus
    pappus
    Bonjour à tous
    Je pense qu’il vaut mieux présenter la formule de GaBuZoMeu comme une inégalité et remplacer le symbole $=$ par le symbole $\le$, l’égalité étant réalisée si et seulement si $B$ appartient au segment $AC$
    Amicalement
    [small]p[/small]appus
    PS
    C’est exactement le même problème avec le théorème de Ptolémée qu’il vaut mieux présenter comme une inégalité (transformation par inversion de l’inégalité triangulaire).
  • pappus
    pappus
    Bonjour à tous
    J’ai peut-être dit des bêtises mais je suis confiné dans ma télègue avec mon iPhone et il m’est difficile de me corriger!
    Amicalement
    [small]p[/small]appus
  • JLT
    JLT
    Autre démonstration avec les nombres complexes : en prenant $O$ comme origine et $(OB)$ comme axe des abscisses, on a $A=fe^{-i\alpha}$, $B=g$, $C=he^{i\beta}$. Alors $A,B,C$ sont alignés si et seulement si la partir imaginaire de $(\overline{A-B})(C-B)$ est nulle. Or $\displaystyle (\overline{A-B})(C-B)=(fe^{i\alpha}-g)(he^{i\beta}-g)=fgh\left(\frac{e^{i(\alpha+\beta)}}{g}-\frac{e^{i\alpha}}{h}-\frac{e^{i\beta}}{f}+\frac{g}{fh}\right)$ et on conclut immédiatement.
  • JLT
    JLT
    L'égalité de GaBuZoMeu dit simplement que l'aire orientée de $AOC$ est égale à la somme des aires orientées de $AOB$ et de $BOC$, il n'y a pas d'inégalité dans un sens ni dans l'autre.
  • Rescassol
    Rescassol
    Bonjour,

    Ça alors, si JLT fait du Morley, où va-t-on ?? :-D

    Cordialement,

    Rescassol
  • pappus
    pappus
    Bonjour à tous
    C’est pas commode de taper du texte sur un iPhone mais je n’ai que cela à faire en attendant mon épouse qui fait des achats dits de première nécessité dans une grande surface.
    Je trouve maintenant que l’astuce de GaBuZoMeu de passer dans l’espace est un peu artificielle!
    Il préfère manipuler des produits vectoriels dans l’espace que des produits mixtes dans le plan.
    Je note $[\bullet ,\bullet]$ le produit mixte de vecteurs dans le plan orienté.
    Alors la fonction $O\mapsto [\overrightarrow{OA},\overrightarrow{OB}]+[\overrightarrow{OB},\overrightarrow{OC}]+[\overrightarrow{OC},\overrightarrow{OA}]$ est constante et vaut $2S(A,B,C)$ où $S(A,B,C)$ est l’aire algébrique du triplet $(A,B,C)$.
    C’est pratiquement la définition de l’aire algébrique!
    Amicalement
    [small]p[/small]appus
    PS
    Voir le cours d’Hadamard écrit dans les années trente
  • GaBuZoMeu
    GaBuZoMeu
    J'ai le réflexe du produit vectoriel, sans doute une déformation parce que j'en mange pas mal ces derniers temps.
    Mais tout ça (produit mixte dans le plan, produit vectoriel dans l'espace) rentre dans le cadre que j'ai signalé plus haut : $\bigwedge ^2(\vec E)$, où $E$ est l'espace affine (de dimension quelconque) où habitent les points $O,A,B,C$.
  • jelobreuil
    jelobreuil
    Bonjour à tous,
    Et un grand merci à tous ! Qu'il est chouette, ce petit exo de rien du tout !
    Pappus, j'aime particulièrement la figure que tu donnes dans ton troisième message ... elle m'inspire plein de jolies choses !
    J'aime bien aussi le calcul de JLT !
    Bon après-midi, bien cordialement
    JLB
  • yan2
    yan2
    Bonjour,

    on a par équivalence :
    \begin{align*}
    A,B,C\,\,\hbox{alignés}
    &\iff [\Delta OAB]+[\Delta OBC]=[\Delta OAC]\\
    &\iff \dfrac{fg\cdot\sin\alpha}{2}+\dfrac{gh\cdot\sin\beta}{2}=\dfrac{fh\cdot\sin(\alpha+\beta)}{2}\\
    &\iff \dfrac{\sin\alpha}{h}+\dfrac{\sin\beta}{f}=\dfrac{\sin(\alpha+\beta)}{g}.
    \end{align*}

    Cordialement,
    Yan2
  • Chaurien
    Chaurien
    J'ai du mal à suivre là. Ce serait Morley qui aurait inventé les nombres complexes ?
  • pappus
    pappus
    Mo cher Chaurien
    Ce ne serait pas plutôt Rescassol?
    Amicalement
    [small]p[/small]appus
Connectez-vous ou Inscrivez-vous pour répondre.

Bonjour!

Pour participer au forum, cliquer sur l'un des boutons :

Connexion S'inscrire

Catégories

In this Discussion

Qui est en ligne 24

GaBuZoMeuJLTLipschitzMrJSethMorleyJuniorchristianmosellerakam +17 Invités