les 3 cercles "inscrits"

Sourire, Bonjour, Au revoir, Merci ?

Bonjour,

L'homothétie de centre \(I\) et de rapport \(\dfrac{IO_1}{IA}\), qui transforme \(ABC\) en \(O_1O_2O_3\), transforme le cercle circonscrit à \(ABC\), de rayon \(R\), en le cercle circonscrit à \(O_1O_2O_3\), de rayon \(TO_1=r\), donc \(\dfrac{r}{R} = \dfrac{IO_1}{IA}\).

L'homothétie de centre \(A\) et de rapport \(\dfrac{AO_1}{AI}\), qui transforme \(I\) en \(O_1\), transforme le cercle inscrit à \(ABC\), de rayon \(R\), en le cercle {\og}inscrit{\fg} de centre \(O_1\), de rayon \(r\), donc \(\dfrac{r}{R'} = \dfrac{AO_1}{AI}\).

On en déduit \(\dfrac{r}{R} + \dfrac{r}{R'} = \dfrac{IO_1}{IA} + \dfrac{AO_1}{AI} = 1\), et les rayons sont liés par la jolie relation :
\[\frac{1}{r} = \dfrac{1}{R} + \dfrac{1}{R'}.

emmanuel487 a écrit:

économie de calculs

C'est dû à mon incommensurable fainéantise naturelle.

Bonjour,
Simple suggestion, tu traces les parallèles à la droite donnée distantes d'icelle du rayon du cercle.

Merci beaucoup pour cette référence.
Le triangle de Malfatti est bien le triangle que je mentionnais. Mais le triangle de Malfatti n'est pas la solution du problème de Malfatti.
Surprenant et pationnant cette histoire! source : mathworld.

In 1803, Malfatti posed the problem of determining the three circular columns of marble of possibly different sizes which, when carved out of a right triangular prism, would have the largest possible total cross section. This is equivalent to finding the maximum total area of three circles which can be packed inside a right triangle of any shape without overlapping. This problem is now known as the marble problem (Martin 1998, p. 92). Malfatti gave the solution as three circles (the Malfatti circles) tangent to each other and to two sides of the triangle. In 1930, it was shown that the Malfatti circles were not always the best solution. Then Goldberg (1967) showed that, even worse, they are never the best solution (Ogilvy 1990, pp. 145-147). Ogilvy (1990, pp. 146-147) and Wells (1991) illustrate specific cases where alternative solutions are clearly optimal.

Je reste intéressé par une réponse à ma première question.
Amicalement.

Pourtant l'idée de Braun est intéressante. On se ramène à chercher un cercle passant par deux points $A$ et $B$ et tangent à une droite $D$. On peut utiliser le point $I$ intersection de $D$ avec la droite $AB$ (quand il existe, sinon la construction est évidente).

Merci à tous.
Le site indiqué par gb est remarquablement bien fait.
Amicalement.

Bonsoir,
Il s'agit de construire un cercle passant par A (et non centré en A). Est-ce que la construction envisagée répond à la question posée ?
Amicalement
Louis

En utilisant la puissance du point \(I\) par rapport à chacun des cercles :
\[\mathcal{P}(I,C) = \overline{IA}.\overline{IB} = -\overline{IA}.\overline{IB'} = -\mathcal{P}(I,C_1) = -\overline{IT}.\overline{IT'} = \overline{IT}^2,\]
donc la droite \((IT)\) est tangente au cercle \(C\) en \(T\).

Bonsoir

Et si on prend l'inversion de pôle A qui transforme B en I.
La droite d est transformée en le cercle D (bleu) passant par A et B et dont le centre O est sur la perpendiculaire à d menée par A.
Les cercles solutions (en rouge) sont transformés en droites passant par I (inverse de et tangents au cercle D (inverse de d) : droites IU et IU' (en pointillé vert). Les points de tangence U et U' sont les transformés de T et T' sur d (A,U,T alignés et A U' T' alignés).
Alain

Bonjour Louis,
Non il n'y a pas d'évidence qui vous échappe! Je ne vois pas comment ramener le second problème au premier.
J'avais posé les 2 questions séparément mais elles ont été regroupées.
Une remarque: le problème 1 a au plus 2 solutions comme il a été dit plus haut, et non 1.

Une façon pas trop compliquée de résoudre le problème 2 est la suivante:

Le truc, c'est que le problème ne demande pas de construire un point, mais un cercle. De ce fait, on ne cherche pas à définir les cercles qui conviennent par leurs centres et un des points A ou B, mais par trois points, et on se focalise sur l'obtention des points T et T'. Toutefois, en cherchant un cercle circonscrit à un triangle, ABT ou ABT', on sait bien que le centre appartient à la médiatrice, propriété que l'on utilisera pour tracer le cercle après avoir construit les points T et T'.

En revenant sur l'appartenance de C a une parabole, cette méthode fournit éventuellement la construction d'un point d'une parabole soumis à une condition supplémentaire.

Bonjour,

Merci pour vos encouragements qui changent des Chalondonades !

Dans la démonstration de gb lire « inscrit à ABC de rayon R' » et non « de rayon R ».


Mes indications de démonstration du cas PPD avec les angles inscrits avait été recopiées sans vérification : je les ai remplacées par la preuve d'Emmanuel.

Voici la figure d'une construction des cercles :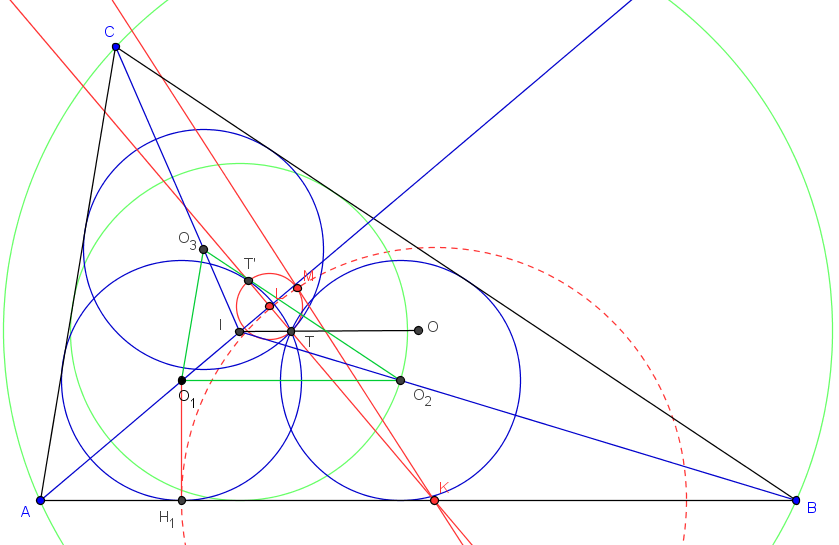



Construction de Wallis

Plus ludique, nous avons fait ci-dessus pour un triangle non isocèle en A, le tracé à partir du point T, sur le segment [IO], que gb a montré comme étant l'image de O par l'homothétie de centre I et de rapport r/R.

Il suffit alors de tracer le cercle passant par le point T, tangent aux côtés [AB] et [AC]. C'est donc un problème PDD que nous ramenons à un problème PPD en construisant le point T’, symétrique de de T par rapport à la bissectrice de l'angle A.

Pour cela, la construction de Wallis, d'un cercle passant par T et T’, tangent à (AB), permet de tracer le point K, intersection de la droite (TT’) avec le côté (AB), et le cercle de diamètre [TT’].

Une tangente, issue de K, coupe ce cercle en M.
Le cercle de centre K, passant par M, coupe le côté [AB] en H1, point de contact du cercle tangent cherché ;
d'où son centre O1 ;
puis les deux autres cercles.

Voir la figure interactive avec GeoGebra.

C'est le problème d'Apollonius : cercle tangent à trois cercles.

C'est un problème assez difficile. Sur mon site je donne une solution par réduction d'un cercle à un point et par inversion.

Est-ce compréhensible ? Quelle est la référence de votre construction par inversion ?

Voici l'image interactive avec GeoGebra, merci à Bruno qui m' adnné la méthode :

<center><applet name="ggbApplet" code="geogebra.GeoGebraApplet" archive="geogebra.jar"
codebase="http://www.geogebra.org/webstart/3.2/unsigned/&quot;
width="600" height="400" mayscript="true">
<param name="ggbBase64" value="UEsDBBQACAAIAKd9hz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VzbbuPIEX3OfgWhhyBBVnR39R2xd2F7F7CwniiYcfYhwWJBS7TMjCwpFDVrzx/lO/JjqWY3ZYmkLpQlezQrwKDVvDXr1OVUdVGn3z8+DINPcTpNxqOzFg1JK4hHvXE/GQ3OWrPsrq1b33/3zekgHg/i2zQK7sbpQ5SdtVgILTs+S7775g+n0/vxb0E0zA/5OYl/O2vdRcNp3AqmkzSO+tP7OM6WxqPZYzJMovSpe/vvuJdNn3e4i3RGkxneJUtnONZ76F8n0+Lrib3hMLqNhzjHD9nTMA6CT9EQp+R23Y1HWRBMk88xPg/YsdOTfJqn8aw3TPpJNLJTyaeNBwXBb0k/u8djOfBWcB8ng3u8lQLtLtcbj9P+h6dpFj8Ej/+M0/FZC6gJKVFANAjJmZKqFTy5XcywUIImRBvOJBC7a9qLhjgXMKEymmsNhisjKMOTVu7Kbx1/+hBnGT7lNIge42cZDdKkv/SlM70YD5+HJuNklF1Gk2yW5jAyP5QL66yFEKf2Ic9Hg2HsxyhK+T7ufbwdP35wkmPu0jdPk/yUfEK3g8vxcJwGKU5ZCDzAb2/dNj/GznR+FMmPIfkR/hr2ovP91EB+RL69dVuHbzJyU/NPTounpqS4TTIN7ABe3Grf/OFzzThrtYLZKMmuiy9Z0vv4/Kj2hL/NHm5R7ReVan5Nuq9rnp6UdO70Y5yO4qFTrBFiOxvPpk593b3yifTjXvKAX90OL5LIwvUPnIAb7ceDNC4m7ozGCSzfSxaVtzR8elJMws5hinPtZWj9+DyZfZabdIxi6MVpbxhPg//9d4C2ag02ux8jYn+PsjTpxcEP8W2UZq2gH2V4jnUF8TB+iNH0slxjcoWbS+6yNfcS49zgC9P2+58xwN212pPrWTSc3Ec4EpLCCzzF6dID59fr3t1N4yx4PGu1KZr0E25hYfe7cX9ZStEIpZ2LAK18Yq9v8ZzEcd97xMwbQTDBO+YmtQBWLuOpvZudl72bttvP7tz8EGd91tk8OypUDSewDaK7eCPROcFR+RqCo9pLrs33KbrzN9M644RnXkN4bdhZeL3xw0M06gej6AHv9CEe2PFcaImNv0FErBCDiFo1dIKaZfMdF+5y/iIVLKb+cnM0nCY/e/bsHh3oKJ5OrYubP+3JeswWRLAKNLI1ZBVMqrYMxAtVP19smyeI/zNyx0xdhEgeJsOkl2RzMQ4tpJ1RhvEizv1vNQx8jOOJjb/d0U0ajaaWerljFsLLCiwxts+GUXqR2IuP0xKmFw5TCy1Y51yGtv8rXY+tFcEcEnv0bsguh9fXgrZNQsklU1wbSRmhRugcahIqab8aDVyBQm7nrUkJw3AHs7sFJXpParArenOLXIkeNEIPjg090EZpTrmWWnNGiHDuj4RGKGKAgERoiQDj8WNaKS5xH2cCR/nB8ZubdQk5ayk5dh6iJdg660FbDm2dnUKb5DkadnPrNs1jGzi/yLdDC0LFQSGtp0QwzQQob2qICVVaCENBUM6VszUSamYUJkCIE2ZP1OhdAtm11e8to1h/UxhbNpadg9jbGMsho9hq+b9L0rTitTpe88+rGHQ2hZuS7vt401y+O+t/cw1vqxAHqDacUAAMM0zsUcPfJX0nk1oZe3kuyfhqU1BYlvGVjwpv4WGkU9m1Kduz/FkIUmJQVoQZIsHHAhaa5Y98CTO+jkeD7L4k7J/z2Pwvv+l8G6DMfvmlIvj3f4wm4+lf1wt/NHuIMa2eC7c4yV4LJzjz0+Qhx0eVDD8co58027sQuv4JLxOb7jckGr31D9UbjxYeqXdA9k8JLBWj8u+7mvZ2jjEZxKNPOfTTIHgkPmV7It7nfi5GHmnOTOw+6oc+0wVFfLD1lMfgvDj+vDjqHEXeFjL/l/mrnnMcy3Plc5FfVtS7acwie8ld0tuAeWxpSgnzXgXlbhO/0X0rr8Fc5WU7n1GUG6wAD+sWut8G53VOoaE7KDsCilxXCi0kMUYxIgV/gSeIHycpKrmtRPj7pa0AB3O5BCfBn9zmffCXwP/nvNOfW8HJxqmn5amzkCqKvhonriVBL7Y3H/ZDMoyysg/rOh+W2mk7P9apoHHTRMNv3krD1RY1pWcV56FkAjMhpQlqCIZIr/CY2TIATRhTSFmk5i8xgFqid1OkOFUScrNNLCyJeyESvgUZ8Wxuy3SHhShzkEwBALI/cFKnIYIgCCY5lDOFgn+h0Gu5nxf7goiXRH/dROjXO/LrYlFI0FzidvNygs1DIrXkAvNEoQ01hUwpJ4YypYETDUijXyDSWvZz7QVapT03W+lxif7cLGryYWjQ7uJfzO9d7Xqtm/mCKBJVIXJ/JaQgGmkfsQs+y3ypRn9y9lTVoBdwqZqSwwaD7G+nRcvlhy9aidYV7WiIAYdqW2slQtN5noYgMMjrqlpJjYCw3I5liDHLEMydCaVCssOXXFeV7M59rXwJriUgf2riWX/aKZDtxbCdXYPYsqwBIgRlKHBDmJJ+GRWTz9AoLoSUnEvhwAJEizPJDJWUSlbcoZkLvolGg+ri009O+L2Vws8G7ohs0KTmjWdtVif6ZVmQCCUVgoFmSPoZA14UOiTVHKmexB3WUCwiDEJ0aEIoJgUogga2jf3Qhga0VsAHXVQ4jIR5yA0wY8UlBeWSFauqhnPAVIUodEoKXZijGphEonQN+incwyl7u2WFZ/PwtlAxk3dNfNS7N/NRjZJ4jqxaAFWCKMZB6IIXLpsJM3snht4pvasSQ9GIEYojcUJbeo1XoXsckEgQieZmDRUYk9XyGAfr9oQSimgjPd3j4QrT247frTQ94ZfSq6saV8Vi39WvrIn5XdUtb7zW4h44ksC2M0FqAz9oBZRRwXTBEvbaxGOltyFK7Fke6x5YhNSyUmWYBskx6O6l86abZvfjwXgUDWvyiLke1ehYnzfJHvhRrV22oVi9LBYvGbp8KZSNxgyDMSixjYN6Ucit74nyOUF1ReTicj0e5Z6oi8tj6olq03mrGZ33OPK5Zz2Gvqi1PW5VPM8b4nl+pHiCR7NN5TGhuVWf1KUr+9c4z01xudQnxY7KfZLQIDfWRnACWmAeT4vOG6MwbcFEHXmy0sTVojGPpJogn2LIqbkEztie1KAhue4UnKnaINXboep68HLZV7v0bEIClutIQrVQVFeIdrXxwi9Kl3oUXrRGvbKTjq9eZeo2ayfq7si3d7PYRbLtaqBrO+wXCnIylISBMEJJQdG0/coU+nBpF/qIwT9J7QtHn3Oiil+ZMZIbLvj8laIXN9J152y0Gi0nTbqGJ0fWNEw1ukiwr2ch+UeRUoceI6EAoowBow3BnFR6qspDwYxkUinbj3r44tBarKrBb9KkXjo5rhbhIm/AWBbWYAOChcSWjjT+Ych7y35gcABNqtGu26xhr/t2DXvN+vWkFKEiGDBAc2mK97MUCxmVBmONBEOEb0vQOuT4YZqDNT2908rCauEzL/y6ENKoZNOtq1G8VsnG+SG6ZRTBHJqA0tQ2XmNw577gI2Voi2lESc0VFN2ShISa2DcfbFODFHynXtVamtcthJ9Wad4m2Zco3s68vGnOBeQFNaQviNoBmhoh3DAhqEG2L8rMDg8AzA9s/4qiSqEFem6HVINTCgqjIGYISsFLqN0KvYDVerHBIZb1Yteg9XvVC65C0Exjaqgl5n/alPVCIdWRSkrGNSqARPhztUAnAdpIQjBhYEZQcQi1oKvVYgPrLKvFrrzz96oWbYnuAOE2UgnUCmRMZb0oLwMwdQjFqC/d+XpBt6IXnQ19y+XSXad7VKU7PBctlEn8oBtnDP25ey8rVNZ0KcZwYphya9X2FWGBWSAw20wjge3tHcZXKPK9j57qC3vVRt6+K/ds8ggpXnFe1pufcgReYblZYbHM4ooBolKSsSwOQsot5BTdtu1toMeDfb3Nz6NBt6ZK2KXdDTyhbPn5GYdGP8d9b70qRYaLqZRmyMYos01ymrj2H/QBhoNCjyxth4o+ImPfCDirA3xDwlAD+OFzhh0Ar3bhrv/5jQV3wEKOSbVWXFOmbSwu3m9Z1g/luysFHoEkDwBdB1FfgX6wNQ4BGusHfJn6sfbFgzr8bfkLyQG1byMobkB7NmBfSGDSADIEENyWko9cAS5WMYKLDW/VVxbkO18DD2jTWhqIuDNM662SKEUo2Vf7xJvBfrkK9suGsF/uCnvjAveecMdUfIn+u3p3Hf1rgwwpaI35GzqCo4f86pkK1LzkTrsbqH8Z+PyMw1n8YRqVy69Q+ncpIEQ3zzmOGBCEUfZjm7pCrrABn6CH0ERaPTj6gL+mS6Cz8ZcOKpn/1Valwp1bcal9T2KhRWBfr8WVfwtgsVXORgCBfgAdvUYOwOY/Z/nyVwAOAvrJ4i8R2u/FD45+939QSwcInKVgrNcMAACiVAAAUEsBAhQAFAAIAAgAp32HP5ylYKzXDAAAolQAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAARDQAAAAA="/>
<param name="image" value="http://www.geogebra.org/webstart/loading.gif&quot; />
<param name="boxborder" value="false" />
<param name="java_arguments" value="-Xmx512m -Djnlp.packEnabled=true" />
<param name="cache_archive" value="geogebra.jar, geogebra_main.jar, geogebra_gui.jar, geogebra_cas.jar, geogebra_export.jar, geogebra_properties.jar" />
<param name="cache_version" value="3.2.47.0, 3.2.47.0, 3.2.47.0, 3.2.47.0, 3.2.47.0, 3.2.47.0" />
<param name="framePossible" value="true" />
<param name="showResetIcon" value="true" />
<param name="showAnimationButton" value="true" />
<param name="enableRightClick" value="false" />
<param name="errorDialogsActive" value="true" />
<param name="enableLabelDrags" value="true" />
<param name="showMenuBar" value="true" />
<param name="showToolBar" value="true" />
<param name="showToolBarHelp" value="false" />
<param name="showAlgebraInput" value="false" />
<param name="allowRescaling" value="true" />
Il semble que cette appliquette Java, créée avec GeoGebra, ne fonctionne pas sur votre ordinateur.
</applet>
</center>